目录
一、前言
二、算法思想
三、代码实现
四、测试
五、源码
一、前言
前两篇学习的Dijkstra算法和Bellman-Ford算法都是用来求解图的单源最短路径,即从图中指定的一个源点出发到图中其他任意顶点的最短路径。Dijkstra算法不能求解带有负权重的图的最短路径,而Bellman-Ford算法弥补了这个缺点。本篇文章再来见识一下一个求解多源最短路径的算法——Floyd-Warshall算法。
多源最短路径–Floyd-Warshall算法
Floyd-Warshall算法是一种解决多源最短路径问题(任意两点间的最短路径)的算法。
Floyd算法又称为插点法,是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法(可以求解带负权的图)。 该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。
我们前面学的Dijkstra算法和Bellman-Ford算法,它们是用来求单源最短路径的,但是我们如果以所有的顶点为起点都走一遍Dijkstra/Bellman-Ford算法的话,其实也可以得到任意两点间的最短距离。 不过呢,Dijkstra算法的话不可以求解带负权路径的图,而Bellman-Ford算法呢效率又有点低。
二、算法思想
Floyd-Warshall算法考虑的是一条最短路径的中间节点:
设k是最短路径p的一个中间节点,那么从i到j的最短路径p就被分成i到k和k到j的两段最短路径p1,p2。 p1是从i到k且中间节点属于{1,2,…,k-1}取得的一条最短路径;p2是从k到j且中间节点属于{1,2,…,k-1}取得的一条最短路径
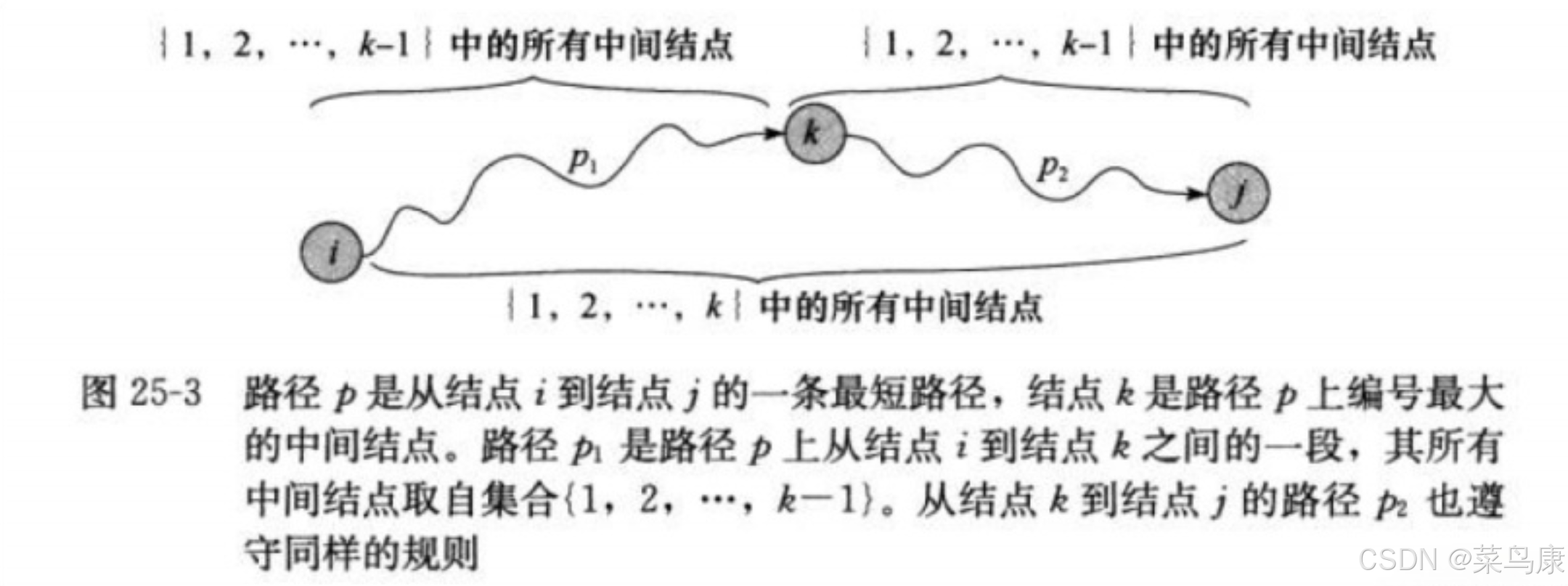 如何去求最短路径p呢?我们先来了解下面的原理
如何去求最短路径p呢?我们先来了解下面的原理
 即Floyd算法本质是三维动态规划,D[i][j][k]表示从点i到点j只经过0到k个点最短路径,然后建立起转移方程,然后通过空间优化,优化掉最后一维度,变成一个最短路径的迭代算法,最后即得到所有点的最短路。
即Floyd算法本质是三维动态规划,D[i][j][k]表示从点i到点j只经过0到k个点最短路径,然后建立起转移方程,然后通过空间优化,优化掉最后一维度,变成一个最短路径的迭代算法,最后即得到所有点的最短路。
上面原理中的这个公式,在动态规划中应该叫状态转移方程:
Di,j,k表示从i到j的最短路径,该路径经过的中间结点是剩余的结点组成的集合中的结点,假设经过k个结点,编号为1…k,然后这里就分为了两种情况:
- 如果路径经过了结点k,那么
ij的距离就等于ik的距离加上kj的距离,然后剩余就经过k-1个点- 如果不经过结点k,那
ij的距离就等于i到j经过k-1个点(不包括k)的距离
那i到j的最短路径就等于这两种情况中的最小值
考虑这里如何存储最短路径和路径权重 ?
前面的两个算法中我们的dist数组和pPath数组都是用了一个一维数组就行了。 但是Floyd-Warshall算法就不一样了,因为前两个算法算的是单源最短路径,而Floyd-Warshall算法是多源最短路径。 因为前面我们都是一个起点,然后求其它顶点到起点的最短路径;而现在是多源,即每个顶点都可以是起点,所以我们要记录每个顶点作为起点时到其它顶点的最短路径距离和路径。 那我们就需要用二维数组了。
三、代码实现
初始化部分
void FloydWarshall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath)
{size_t n = _vertexs.size(); // 获取图中顶点数量vvDist.resize(n); // 调整距离矩阵大小为n*nvvpPath.resize(n); // 调整路径矩阵大小为n*n// 初始化权值和路径矩阵
for (size_t i = 0; i < n; ++i) {vvDist[i].resize(n, MAX_W); // 距离初始化为无穷大(MAX_W)vvpPath[i].resize(n, -1); // 路径初始化为无效值(-1)
}接着 我们要把图中所有相连的边的信息直接更新一下,因为上面我们说了那个公式叫做状态转移方程,而这里初始化更新的结果就作为起始状态,后面通过状态转移方程不断更新得到最终结果

// 直接相连的边更新
for (size_t i = 0; i < n; ++i) {for (size_t j = 0; j < n; ++j) {if (_matrix[i][j] != MAX_W) { // 存在直接边vvDist[i][j] = _matrix[i][j]; // 更新直接距离vvpPath[i][j] = i; // 记录前驱为起点i}if (i == j) { // 对角线处理vvDist[i][j] = W(); // 自身距离设为0(W()生成零值)}}
}根据状态转移方程更新
// 最短路径更新:i-> {其他顶点} ->j
for (size_t k = 0; k < n; ++k) { // 中间顶点kfor (size_t i = 0; i < n; ++i) { // 起点ifor (size_t j = 0; j < n; ++j) { // 终点j// 尝试通过k中转更新路径
//如果:
//1. ik是相连的
//2. kj是相连的
//3. ik+kj的距离(经过k点)小于ij(不经过k点)的距离,就更新为ik+kj的距离,否则不更新,保存原来不经过k点的距离
//其实就是前面我们给出的状态转移方程的判断(取两者之间小的那一个) if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W&& vvDist[i][k] + vvDist[k][j] < vvDist[i][j]) {// 更新最短距离vvDist[i][j] = vvDist[i][k] + vvDist[k][j];// 更新路径前驱(关键步骤!)//注意:这里j的上一个结点不能之间给k,因为k->j路径上k和j不一定之间相连,//有可能也更新了中间结点(k->...->j),//而kj路径上的j的上一个是誰?就存储在vvpPath[k][j]里面vvpPath[i][j] = vvpPath[k][j];}}}四、测试
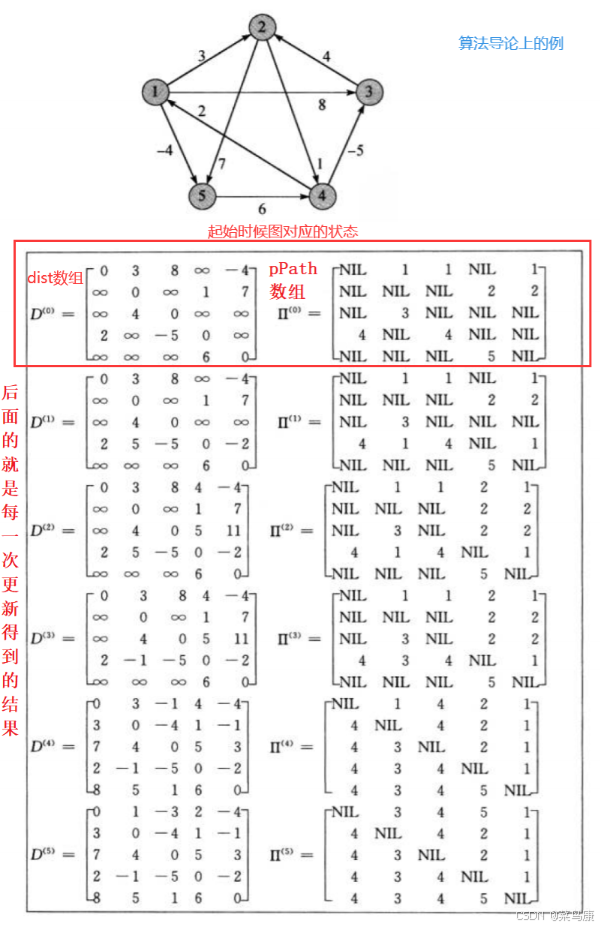
加一个打印权值和路径的二维数组的代码,因为上面那个例子也是把每一步对应的两个二维数组(矩阵)画了出来,我们可以打印(每个顶点作为中间结点更新之后的都打印一下)出来观察对比一下:
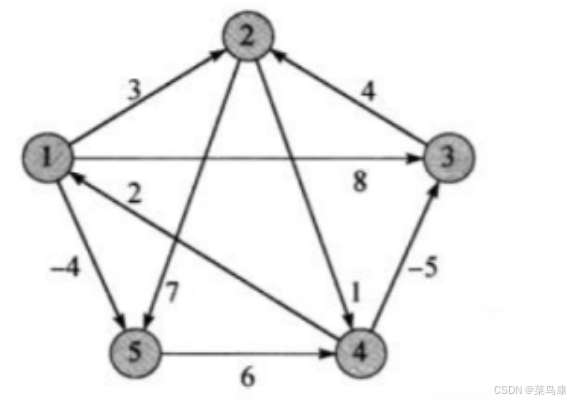
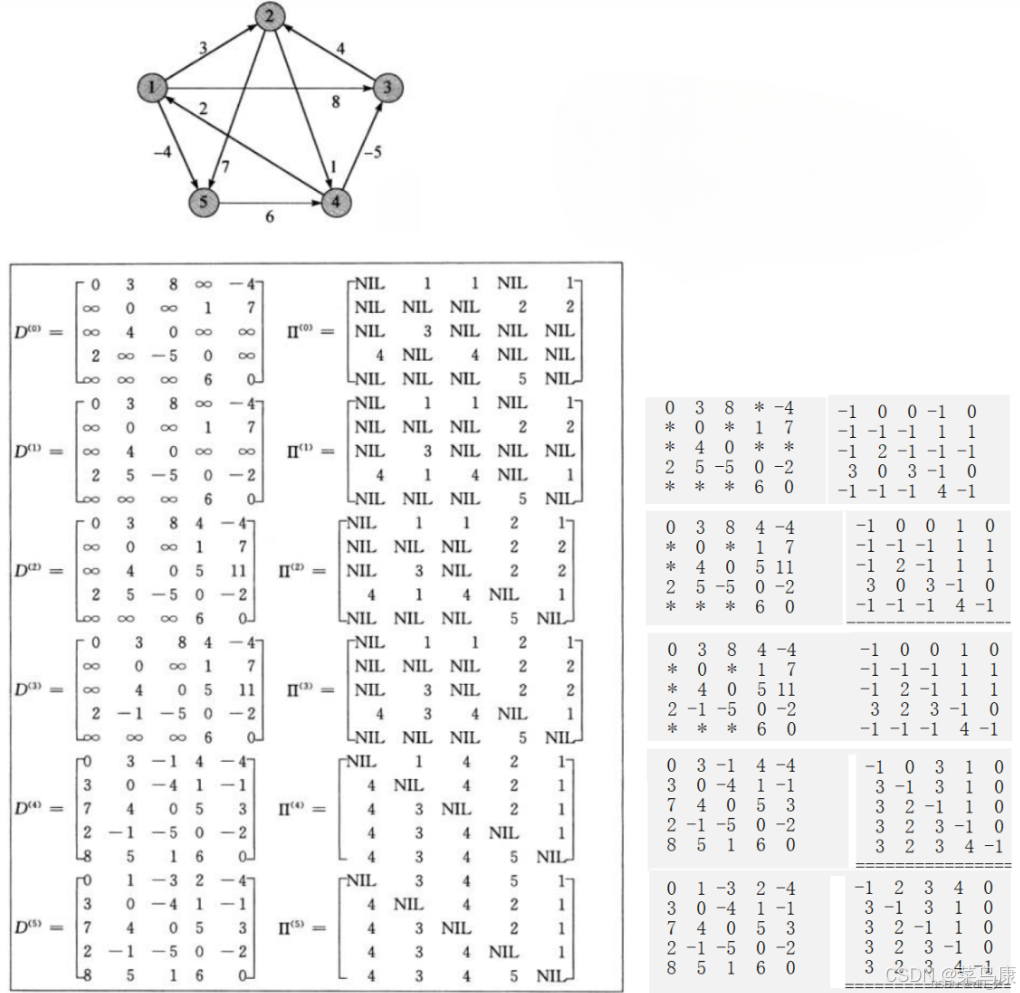
// 打印权值和路径矩阵观察数据for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){if (vvDist[i][j] == MAX_W){//cout << "*" << " ";printf("%3c", '*');}else{//cout << vvDist[i][j] << " ";printf("%3d", vvDist[i][j]);}}cout << endl;}cout << endl;for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){//cout << vvParentPath[i][j] << " ";printf("%3d", vvpPath[i][j]);}cout << endl;}cout << "=================================" << endl;void TestFloydWarShall(){const char* str = "12345";Graph<char, int, INT_MAX, true> g(str, strlen(str));g.AddEdge('1', '2', 3);g.AddEdge('1', '3', 8);g.AddEdge('1', '5', -4);g.AddEdge('2', '4', 1);g.AddEdge('2', '5', 7);g.AddEdge('3', '2', 4);g.AddEdge('4', '1', 2);g.AddEdge('4', '3', -5);g.AddEdge('5', '4', 6);vector<vector<int>> vvDist;vector<vector<int>> vvParentPath;g.FloydWarshall(vvDist, vvParentPath);}还是使用上面的图解中的图
运行结果
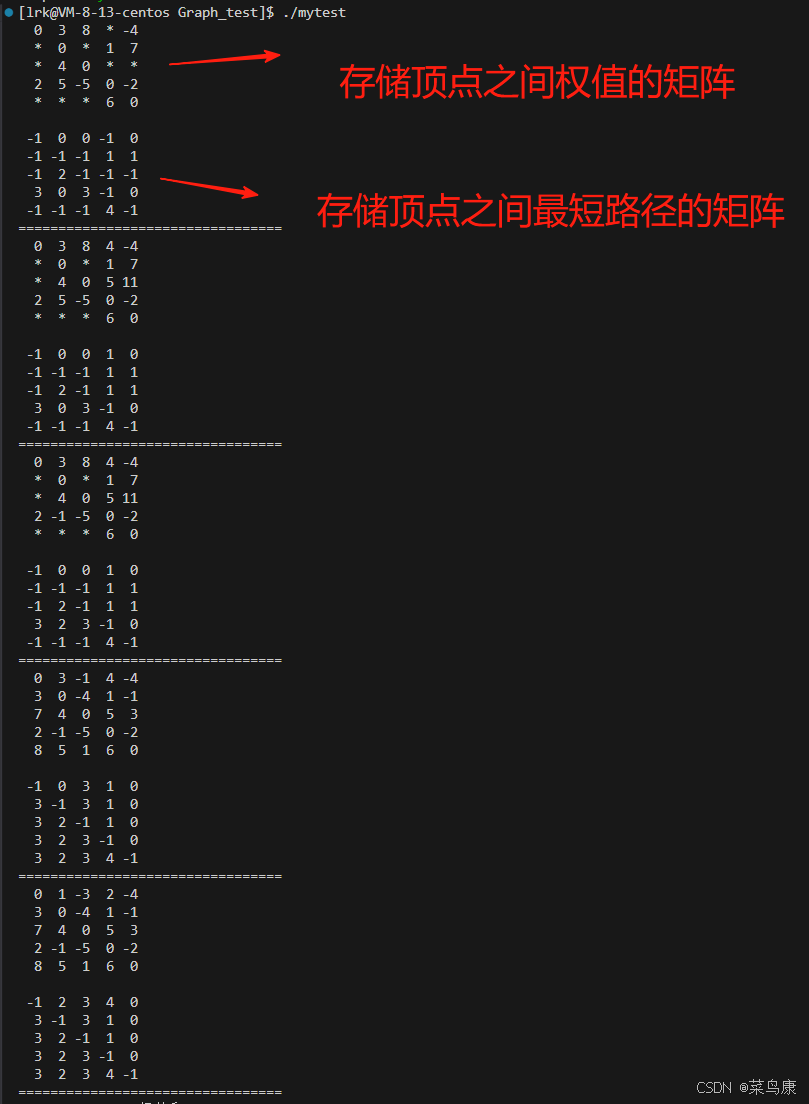
为了方便对比
∞等价于* NIL等价于-1
另外pPath数组例子中给的直接就是结点本身(他这里的顶点就是1 2 3 4 5),我们用的是顶点映射的下标,所以大家看到比他的值小1
接着我们打印一下任意两个顶点之间的最短路径
// 打印任意两点之间的最短路径for (size_t i = 0; i < strlen(str); ++i){g.PrintShortPath(str[i], vvDist[i], vvParentPath[i]);cout << endl;}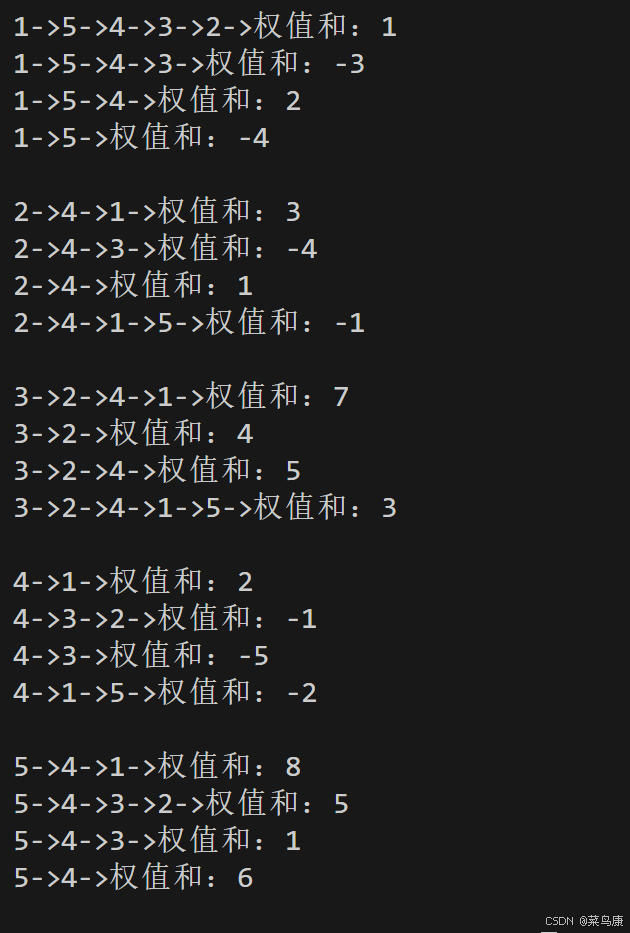
五、源码
void FloydWarshall(vector<vector<W>>& vvDist, vector<vector<int>>& vvpPath){size_t n = _vertexs.size();vvDist.resize(n);vvpPath.resize(n);// 初始化权值和路径矩阵for (size_t i = 0; i < n; ++i){vvDist[i].resize(n, MAX_W);vvpPath[i].resize(n, -1);}// 直接相连的边更新一下for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){if (_matrix[i][j] != MAX_W){vvDist[i][j] = _matrix[i][j];vvpPath[i][j] = i;}if (i == j){vvDist[i][j] = W();}}}// abcdef a {} f || b {} c// 最短路径的更新i-> {其他顶点} ->jfor (size_t k = 0; k < n; ++k){for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){// k 作为的中间点尝试去更新i->j的路径if (vvDist[i][k] != MAX_W && vvDist[k][j] != MAX_W&& vvDist[i][k] + vvDist[k][j] < vvDist[i][j]){vvDist[i][j] = vvDist[i][k] + vvDist[k][j];// 找跟j相连的上一个邻接顶点// 如果k->j 直接相连,上一个点就k,vvpPath[k][j]存就是k// 如果k->j 没有直接相连,k->...->x->j,vvpPath[k][j]存就是xvvpPath[i][j] = vvpPath[k][j];}}}// 打印权值和路径矩阵观察数据for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){if (vvDist[i][j] == MAX_W){//cout << "*" << " ";printf("%3c", '*');}else{//cout << vvDist[i][j] << " ";printf("%3d", vvDist[i][j]);}}cout << endl;}cout << endl;for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){//cout << vvParentPath[i][j] << " ";printf("%3d", vvpPath[i][j]);}cout << endl;}cout << "=================================" << endl;} }感谢阅读!
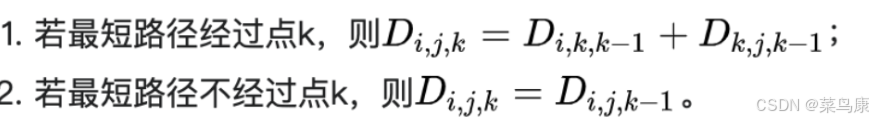
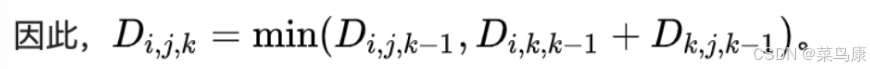
 打不开,无网络连接的问题!)






 视频教程 - 词云图-微博评论词云图实现)

、内核链表、栈(系统栈、实现方式)、队列(实现方式、应用))
:windows安装使用node.js 安装express,suquelize,sqlite,nodemon)

![[Python 基础课程]猜数字游戏](http://pic.xiahunao.cn/[Python 基础课程]猜数字游戏)


)



)