1.公式推导

1.1两个问题

ICA算法会带来2个不确定性：

        幅值不确定性和顺序不确定性。

1.2 推导

观测数据 x 是盲源 s 的线性混合：x = As               (1)

        此时，W矩阵是未知的，ICA算法的目的便是找到一个最优的矩阵W，实现对矩阵S^的求解。如果直接采用线性代数的方法对(2)式进行求解，显然是不可行的。因此需要增加额外的条件让(2)式更容易求解。

        ICA算法通过假设Si 为两两相互独立的随机变量，由矩阵A变换后，成为两两非相互独立的随机变量Xi从而进行求解。这个条件也限制了Xi中最多只能有一个呈高斯分布的随机变量，否则，就不能满足Xi之间两两非相互独立的条件。 

上文解释：

        当独立的源信号 Si​ 被混合矩阵 A 线性组合后，得到的观测信号 Xi​ 会失去独立性，变成 “两两非相互独立”。ICA 的求解逻辑就是 “源信号 Si​ 独立 → 混合后 Xi​ 非独立”，进行反向操作：

1. 从观测信号 X（非独立）出发，假设它由 “独立源 S 混合” 而来；
2. 通过算法寻找一个 “解混矩阵 W”（即你提到的 W 矩阵 ），使得 W⋅X 的结果尽可能接近 “独立的源信号 S”；
3. 最终，当 W⋅X 恢复出 “两两独立” 的特性时，就认为找到了源信号 S 的近似解 S^。

 为什么限制 “最多一个高斯分布”？

        如果源信号 Si​ 中有两个或以上是高斯分布，混合后的观测信号 Xi​ 会因 “高斯分布的线性组合仍为高斯分布”，导致 Xi​ 之间的 “非独立性” 无法区分（数学上，多个独立高斯信号混合后，无法通过统计方法唯一解混 ）。因此，ICA 要求源信号 Si​ 中最多一个是高斯分布，才能保证混合后的 Xi​ 有 “可解混” 的非独立性。        

限制一个高斯分布的证明过程：

        已知高斯分布的概率密度函数是：

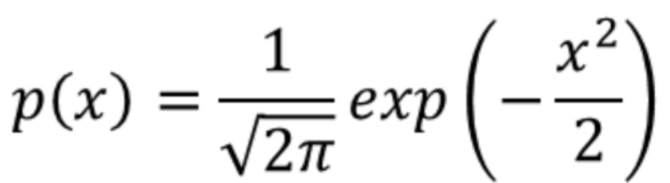
        假设混合信号x1，x2都满足高斯分布，其联合概率分布函数可以写成：

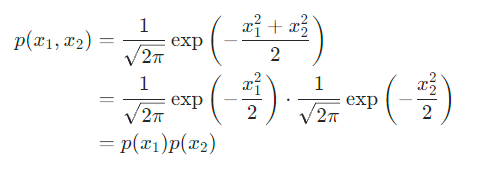
        根据概率论中对相互独立的定义，x1，x2相互独立，从而无法满足ICA算法中，混合信号xi之间两两非相互独立的要求。

继续证明：

        ICA 算法的目的是得到两两相互独立的Si​，因此需要对求解结果之间的独立性进行评结，评估的方式是对结果的非高斯性进行量化评估。

        根据 (3) 式，X由多独立成分混合成的，为了简化问题，假设这些独立成分有相同的分布。现在考虑其中一个独立成分的求解。

        此时，y 可以视为 Si​ 的线性组合。根据中心极限定理 (多个独立随机变量的线性组合/或均值，其分布会随着组合项数的增加，逐渐趋近于高斯分布)，y 比任何一个 Si​ 都更加接近高斯分布。通过寻找一个 w，让 wT·x 的高斯性尽可能的低，从而让 y 接近某个 Si​，这是 ICA 算法的核心思路。最理想的情况是向量中只有一个非零值，此时，y 就等价于某个 s。

        对随机变量的非高斯性进行量化评价通常有以下几种方法，假设随机变量 y 的期望为 0，方差为 1。

1.3 评估随机变量的非高斯性（峰度）

假设随机变量的期望为0，方差为1

1.峰度
峰度定义为：

通过假设y的方差为 1，(8) 式可以简化为:

若y符合高斯分布，则峰度kurt(y)=0，对于大多数非高斯随机变量为非零值。

峰度有以下性质：对于两个独立的随机变量x1​,x2​，有：

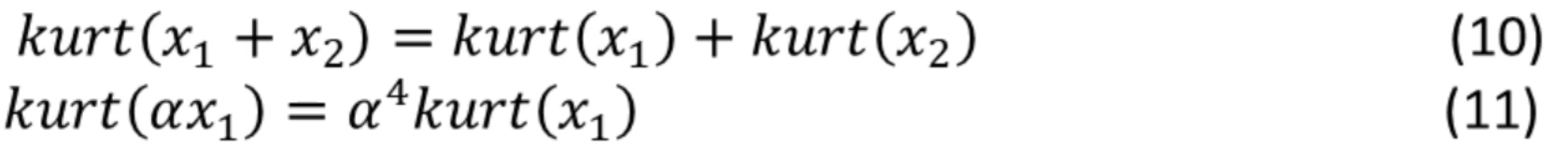
假设有独立成分 s1​,s2​，有峰度 kurt(s1​)，kurt(s2​)，寻找其中的一个独立成分y：

根据（式7），且（独立成分的方差为1，期望为0，Si的平方的期望为1）

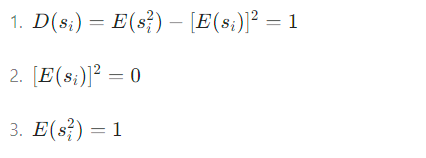
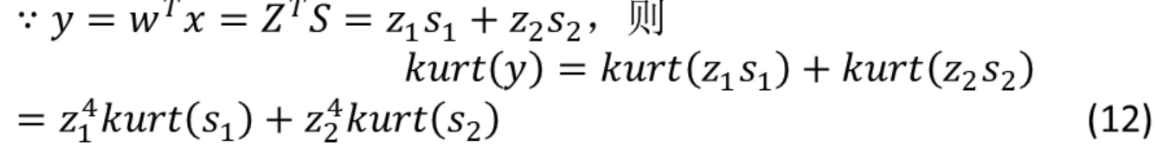
独立成分的方差为1，期望为0，即

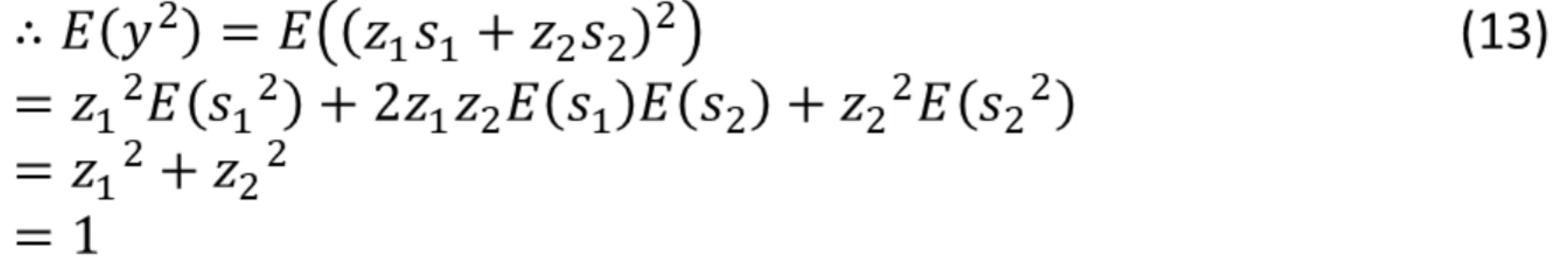
 由 (12) 式得：

        通过让 (14) 式的值最大化，减小y的高斯性。最理想的情况下，z1​，z2​中一个为 0，一个非零。此时，非零的zi​等于 1 或 - 1，y等价于某个±si​。

        实际应用中，需要计算∣kurt(y)∣到最大值的梯度，从而迭代w的值，然而峰值并不是衡量高斯性的最好方法 。

1.4 评估随机变量的非高斯性（负熵）

负熵定义：

其中，Ygaussian​ 是与 y 有相同协方差矩阵的随机变量。

        负熵总是非负的，当 y 是高斯分布时，负熵为 0。这是对高斯性的最佳衡量方式，缺点是计算复杂，因此可以使用一些近似的方法求负熵。  

1.4.1 高阶矩

假设y期望为0，方差为1，则：

1.4.2 最大熵近似原理 

假设y期望为0，方差为1，则：

其中，v为高斯变量，G为非二次函数，需自行定义。一些比较好的G如下所示：

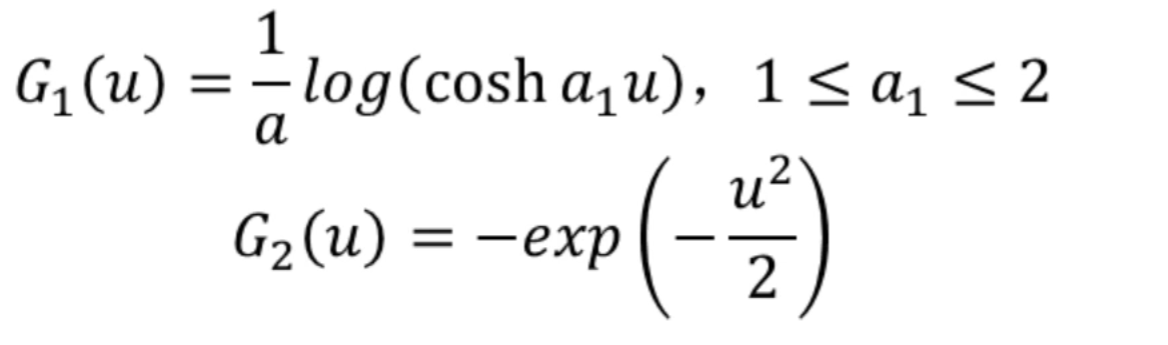
1.5 最小化互信息

见文 ICA学习（1）的 6. 最小化多重信息的简化部分

总结：最下化互信息即最大化负熵。

2. ICA的预处理

2.1 中心化

        中心化是非常基础，也是很有必要的预处理过程。假设向量 x 的期望是 m，将向量 x 的所有元素减去 m，可以使向量 x 的均值变为 0。中心化可以表达为：

        E(x−E(x))=0                    （26）

2.2 白化处理