区间树:多维数据的高效查询
大家好,今天我们来探讨一个在计算机科学中非常有趣且实用的数据结构——区间树。想象一下,你是一位城市规划师,需要快速找出某个区域内所有的医院、学校或商场。或者你是一位游戏开发者,需要高效检测游戏中的碰撞区域。这些场景都需要对区间数据进行快速查询,这正是区间树大显身手的地方。
区间树(Interval Tree)是一种特殊的二叉搜索树,专门用于存储和查询区间数据。与普通二叉搜索树不同,区间树的每个节点存储的是一个区间而非单个值。这种数据结构能够高效地回答诸如"哪些区间与给定区间重叠"这样的查询问题,时间复杂度可以达到O(log n + m),其中n是存储的区间数量,m是查询结果的数量。
1. 区间树的基本概念
理解了区间树的应用场景后,我们来看看它的基本结构和原理。区间树的核心思想是将区间按照某种规则组织起来,使得查询时可以快速排除大量不相关的区间,只检查那些可能与查询区间重叠的候选区间。
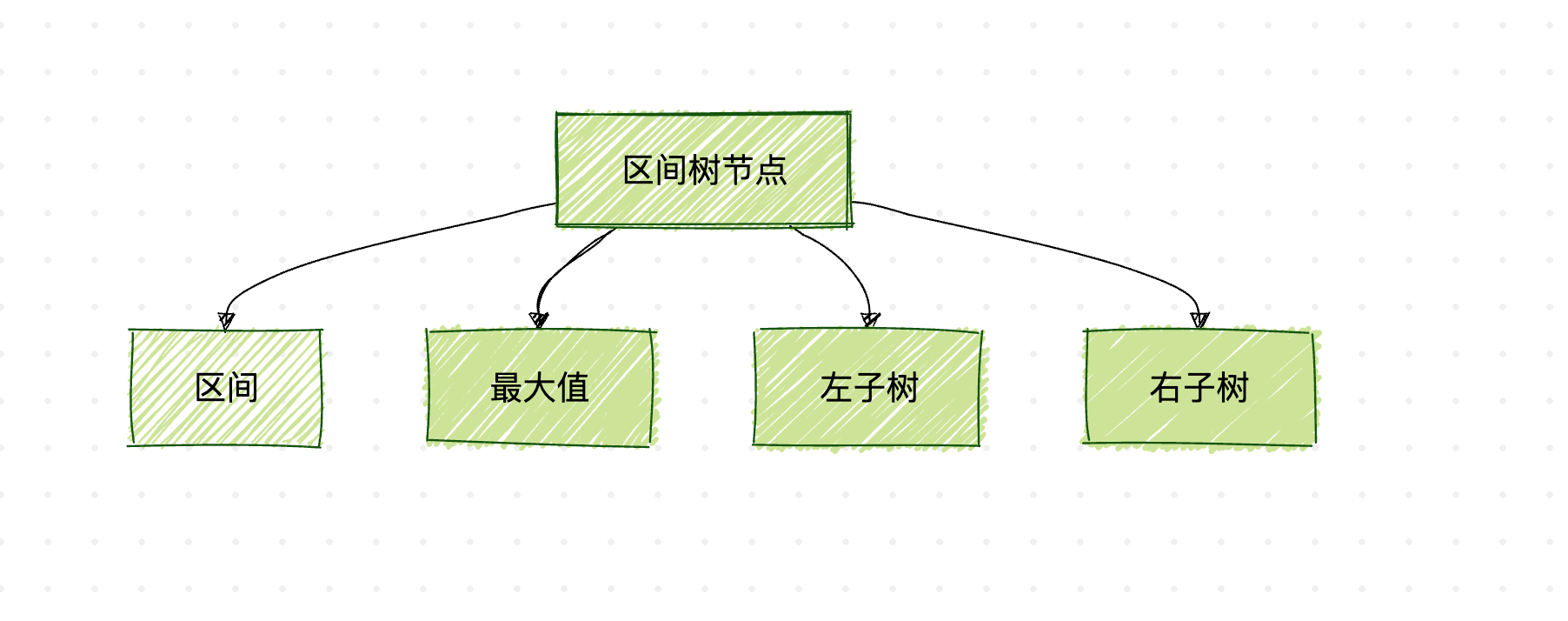
以上图表展示了一个基本的区间树节点结构,包含区间信息、最大值以及左右子树指针。
区间树的每个节点包含三个关键部分:
- 区间信息:通常用[lower, upper]表示
- 最大值:该节点及其子树中所有区间的最大上界
- 左右子树指针
1.1 区间树的构建
让我们通过一个简单的例子来看看如何构建区间树。假设我们有以下区间需要存储:
[15, 20], [10, 30], [17, 19], [5, 20], [12, 15], [30, 40]
构建区间树的过程与构建二叉搜索树类似,但比较的是区间的中点值。下面是构建步骤:
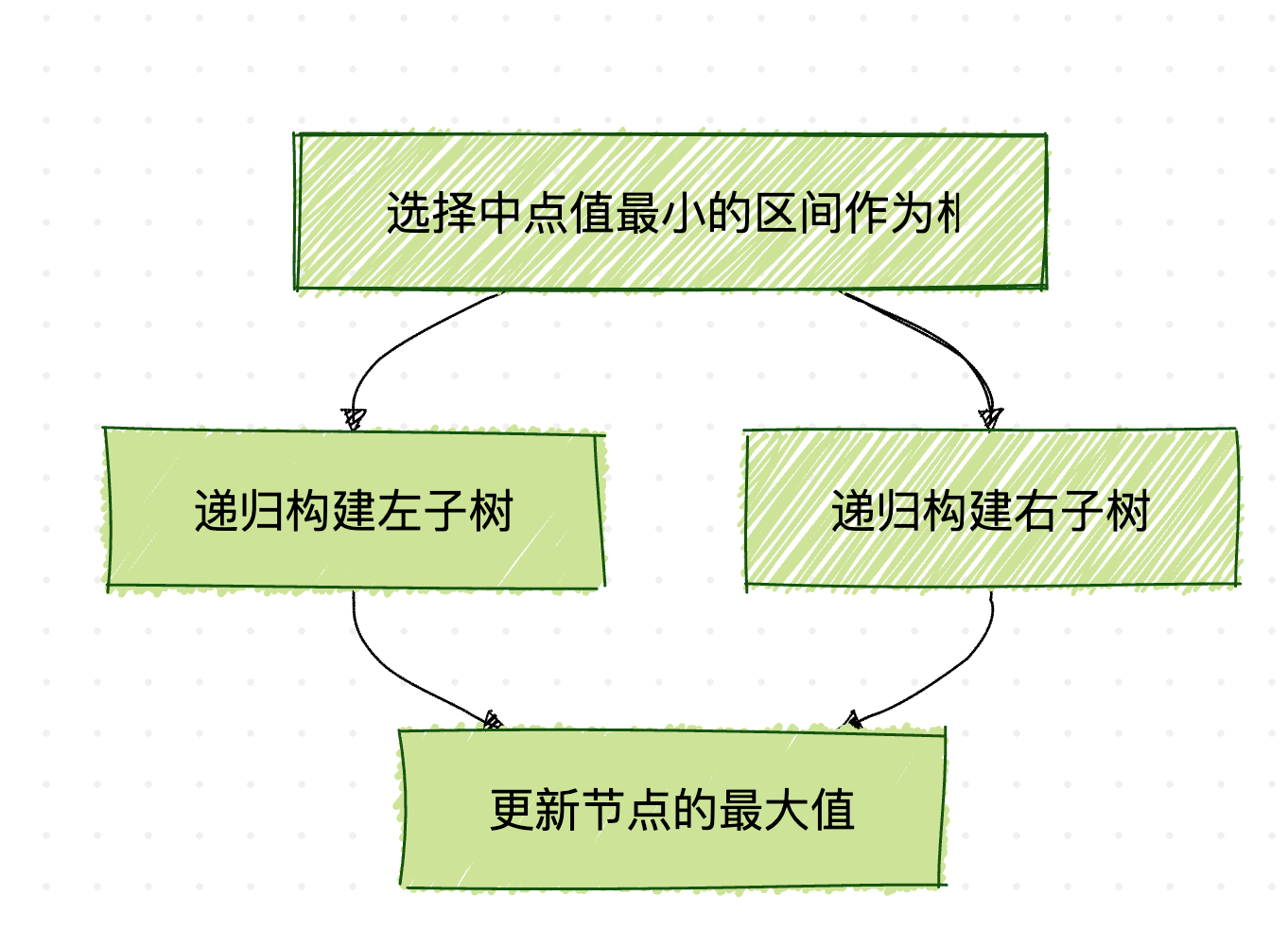
以上流程图展示了区间树的基本构建过程,通过递归方式构建左右子树并更新最大值。
1.2 区间树的查询
区间树最强大的功能是能够高效查询与给定区间重叠的所有区间。查询算法如下:
function queryIntervalTree(node, queryInterval, results):if node is null:return# 检查当前节点区间是否与查询区间重叠if node.interval overlaps with queryInterval:add node.interval to results# 决定搜索方向if left child exists and left.max >= queryInterval.lower:queryIntervalTree(node.left, queryInterval, results)if right child exists and node.interval.lower <= queryInterval.upper:queryIntervalTree(node.right, queryInterval, results)
上述代码展示了区间树查询的基本算法,通过递归方式检查重叠区间并根据条件决定搜索方向。
2. 区间树的实现
了解了区间树的基本原理后,我们来看看如何用代码实现一个简单的区间树。我们将使用Python来实现这个数据结构。
2.1 Python实现
class IntervalTreeNode:def __init__(self, interval):self.interval = intervalself.max = interval[1]self.left = Noneself.right = Noneclass IntervalTree:def __init__(self):self.root = Nonedef insert(self, interval):if not self.root:self.root = IntervalTreeNode(interval)returncurrent = self.rootwhile True:# 更新当前节点的最大值current.max = max(current.max, interval[1])# 决定插入方向if interval[0] < current.interval[0]:if current.left is None:current.left = IntervalTreeNode(interval)breakelse:current = current.leftelse:if current.right is None:current.right = IntervalTreeNode(interval)breakelse:current = current.rightdef query_overlap(self, query_interval):results = []self._query_overlap(self.root, query_interval, results)return resultsdef _query_overlap(self, node, query_interval, results):if node is None:return# 检查重叠if self._is_overlap(node.interval, query_interval):results.append(node.interval)# 决定搜索方向if node.left and node.left.max >= query_interval[0]:self._query_overlap(node.left, query_interval, results)if node.right and node.interval[0] <= query_interval[1]:self._query_overlap(node.right, query_interval, results)@staticmethoddef _is_overlap(a, b):return a[0] <= b[1] and b[0] <= a[1]
这段Python代码实现了一个基本的区间树,包括插入和查询功能。通过维护每个节点的最大值属性,可以高效地进行区间重叠查询。
2.2 使用示例
让我们看看如何使用这个区间树实现:
# 创建区间树
itree = IntervalTree()# 插入区间
intervals = [[15, 20], [10, 30], [17, 19], [5, 20], [12, 15], [30, 40]]
for interval in intervals:itree.insert(interval)# 查询重叠区间
query = [18, 25]
result = itree.query_overlap(query)
print(f"与区间{query}重叠的区间有:{result}")
这个示例展示了如何创建区间树、插入区间数据以及查询与给定区间重叠的所有区间。
3. 区间树的变体与应用
理解了基本区间树的实现后,我们来看看一些常见的变体和实际应用场景。
3.1 线段树(Segment Tree)
线段树是区间树的一种变体,主要用于处理区间查询和区间更新问题。与区间树不同,线段树通常用于处理固定范围内的区间,并且支持高效的区间更新操作。
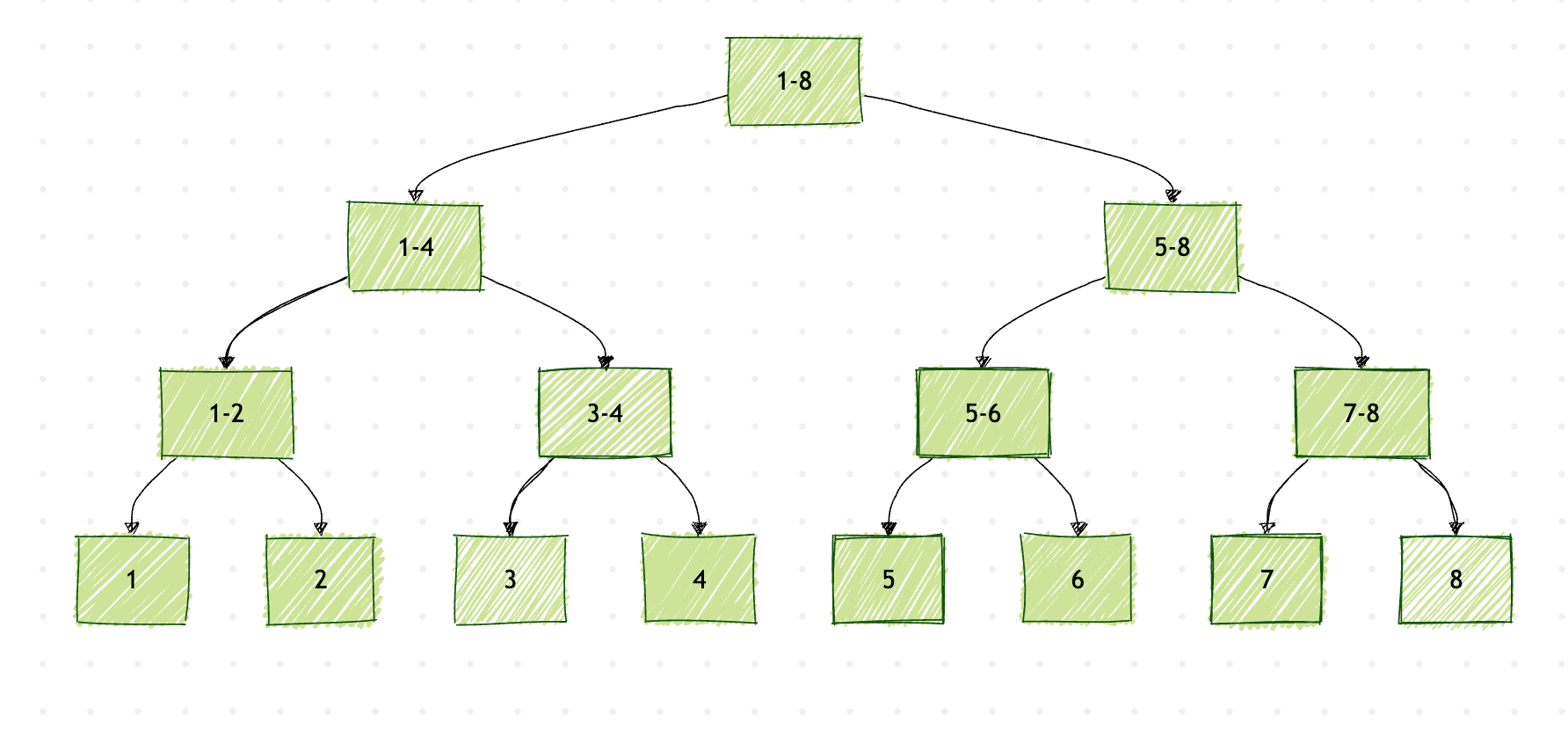
这个线段树示例展示了如何将区间[1-8]递归地划分为更小的子区间,直到每个区间只包含一个元素。
3.2 实际应用场景
区间树及其变体在计算机科学中有广泛的应用:
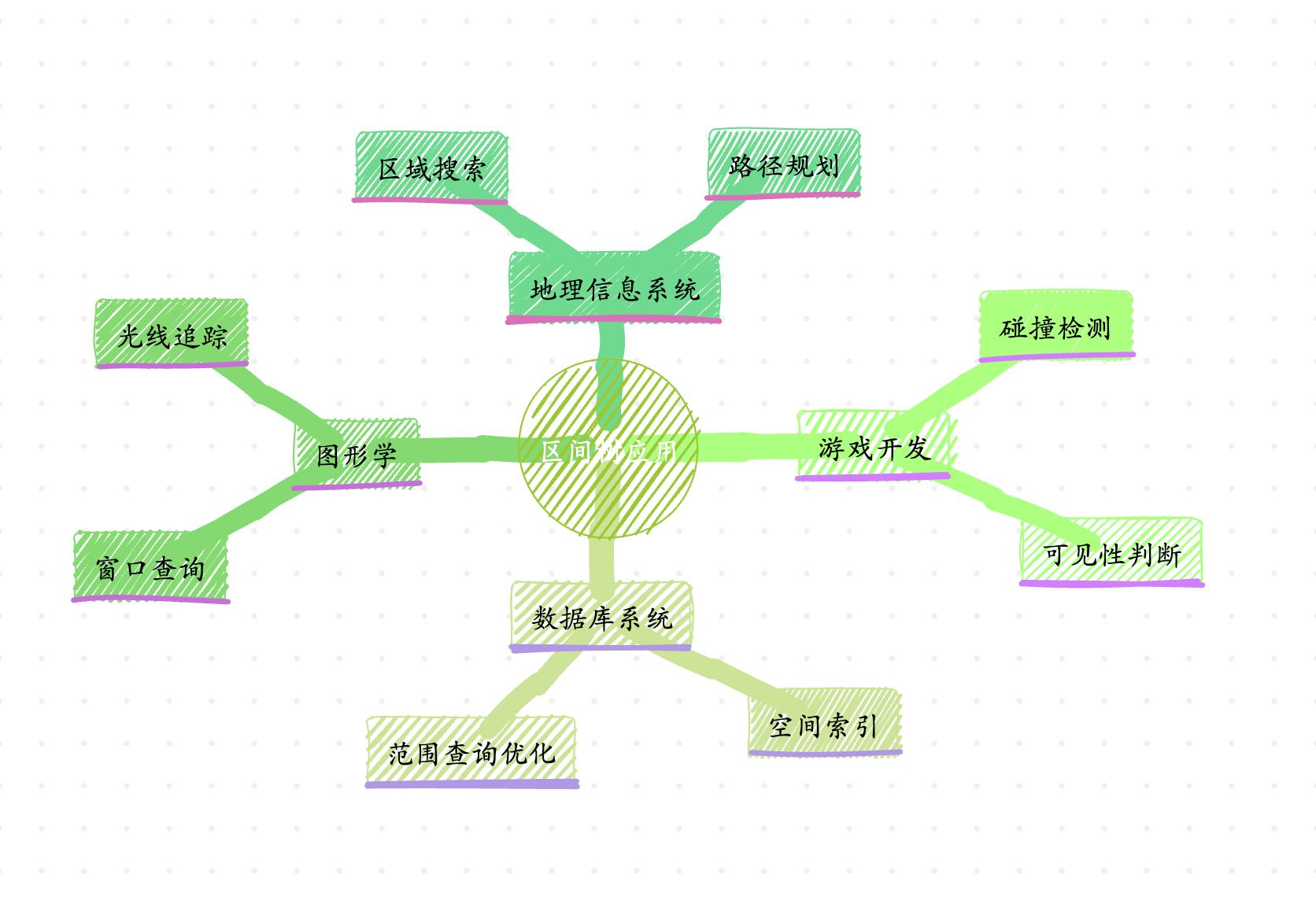
这个思维导图展示了区间树在不同领域的应用场景,从游戏开发到地理信息系统都有广泛用途。
4. 性能分析与优化
了解了区间树的应用后,我们来看看它的性能特点和可能的优化方向。
4.1 时间复杂度
区间树的主要操作时间复杂度如下:

这个甘特图展示了区间树不同操作的时间复杂度对比,其中构建需要O(n log n),查询和插入都是O(log n)。
4.2 空间复杂度
区间树的空间复杂度为O(n),因为需要存储n个区间。在实际应用中,可以考虑以下优化:
- 使用更紧凑的节点表示
- 实现惰性删除策略
- 对静态数据集使用更高效的构建算法
5. 总结
通过今天的讨论,我们深入了解了区间树这一强大的数据结构。让我们回顾一下本文的主要内容:
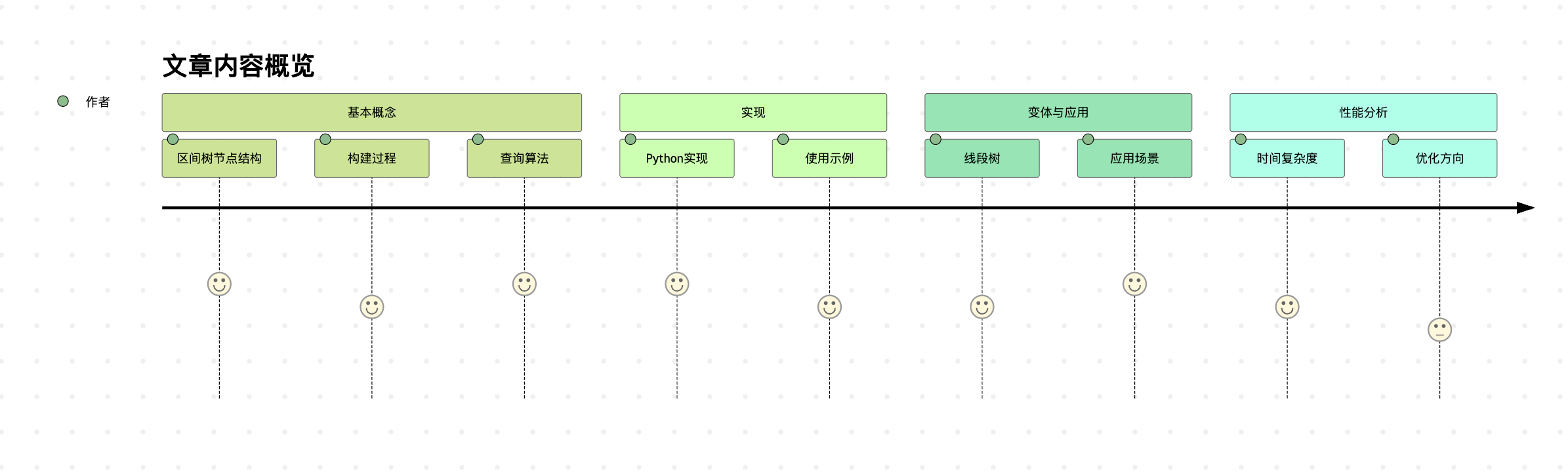
这个旅程图总结了本文的主要内容,从基本概念到实际应用,全面覆盖了区间树的各个方面。
区间树是一种非常实用的数据结构,特别适合处理区间查询问题。通过合理的设计和实现,它可以为我们的应用程序提供高效的区间操作能力。希望大家通过这篇文章对区间树有了更深入的理解,能够在实际项目中灵活运用。
如果你有任何问题或想法,欢迎随时交流讨论。让我们共同进步,探索更多高效的数据结构和算法!















)
 - 一个简单web项目-实现链路跟踪)


