4.3 数值微分
梯度法使用梯度的信息决定前进的方向。本节将介绍梯度是什么、有什么性质等内容。
4.3.1 导数
假如你是全程马拉松选手,在开始的10分钟内跑了2千米。如果要计算此时的奔跑速度,则为2/10 = 0.2[千米/分]。也就是说,你以1分钟前进0.2千米的速度(变化)奔跑。
在这个马拉松的例子中,我们计算了“奔跑的距离”相对于“时间”发生了多大变化。不过,这个10分钟跑2千米的计算方式,严格地讲,计算的是10分钟内的平均速度。而导数表示的是某个瞬间的变化量。因此,将10分钟这一时间段尽可能地缩短,比如计算前1分钟奔跑的距离、前1秒钟奔跑的距离、前0.1秒钟奔跑的距离……这样就可以获得某个瞬间的变化量(某个瞬时速度)。
综上,导数就是表示某个瞬间的变化量。它可以定义成下面的式子。
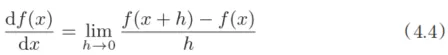
式(4.4)表示的是函数的导数。左边的符号
![]()
表示f(x)关于x的导数,即f(x)相对于x的变化程度。式(4.4)表示的导数的含义是,x的“微小变化”将导致函数f(x)的值在多大程度上发生变化。
如果直接实现式(4.4)的话,向h中赋入一个微小值,就可以计算出来了。比如,下面的实现如何?
![]()
![]()
函数numerical_diff(f, x)的名称来源于数值微分A 的英文numerical differentiation。这个函数有两个参数,即“函数f”和“传给函数f的参数x”。乍一看这个实现没有问题,但是实际上这段代码有两处需要改进的地方。
![]()
如上所示,如果用float32类型(32位的浮点数)来表示1e-50,就会变成0.0,无法正确表示出来。也就是说,使用过小的值会造成计算机出现计算上的问题。这是第一个需要改进的地方,即将微小值h改为
![]()
。使用
![]()
就可以得到正确的结果。
第二个需要改进的地方与函数f的差分有关。虽然上述实现中计算了函数f在x+h和x之间的差分,但是必须注意到,这个计算从一开始就有误差。如图4-5所示,“真的导数”对应函数在x处的斜率(称为切线),但上述实现中计算的导数对应的是(x + h)和x之间的斜率。因此,真的导数(真的切线)和上述实现中得到的导数的值在严格意义上并不一致。这个差异的出现是因为h不可能无限接近0。

数值微分含有误差。为了减小这个误差,我们可以计算函数f在(x + h)和(x − h)之间的差分。因为这种计算方法以x为中心,计算它左右两边的差分,所以也称为中心差分(而(x + h)和x之间的差分称为前向差分)
让我们用一个简单的类比来理解:
想象你开车,想知道在下午3:00整这一瞬间的瞬时速度(这就是“真的导数”)
方法A(前向差分):你记录下3:00的里程表读数,然后开到3:01再记录一次读数,用里程差除以1分钟。你得到的是3:00到3:01这1分钟内的平均速度,而不是3:00整的瞬时速度。这个平均速度可能接近,但绝不等于瞬时速度。
方法B(中心差分):你记录下2:59的里程表读数,然后开到3:01再记录一次读数,用里程差除以2分钟。你得到的是2:59到3:01这2分钟内的平均速度,而这个平均速度的中心点正好是3:00。由于你的速度不太可能在这2分钟内剧烈波动,这个以3:00为中心的平均速度,通常会比方法A得到的那个从3:00开始的平均速度,更能准确地反映3:00整的瞬时速度。
函数定义如下

4.3.2 数值微分的例子
现在我们试着用上述的数值微分对简单函数进行求导。先来看一个由下式表示的2次函数。
![]()
用Python来实现式(4.5),如下所示。
![]()
接下来,我们来绘制这个函数的图像。画图所用的代码如下

图像如下
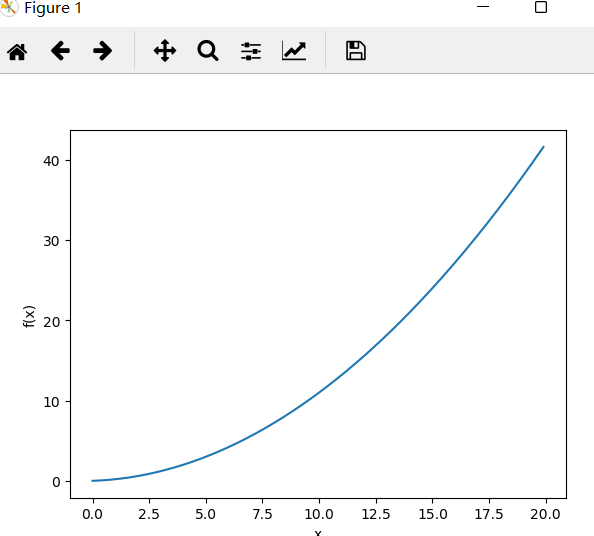
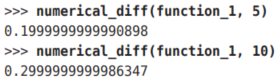
我们来计算一下这个函数在x = 5和x = 10处的导数。
这里计算的导数是f(x)相对于x的变化量,对应函数的斜率。另外,f(x) = 0.01x2 + 0.1x 的解析解是
![]()
。因 此,在 x = 5 和x = 10处,“真的导数”分别为0.2和0.3。和上面的结果相比,我们发现虽然严格意义上它们并不一致,但误差非常小。实际上,误差小到基本上可以认为它们是相等的。
4.3.3 偏导数
接下来,我们看一下式(4.6)表示的函数。虽然它只是一个计算参数的平方和的简单函数,但是请注意和上例不同的是,这里有两个变量。
![]()
这个式子可以用Python来实现,如下所示。
![]()
这里,我们假定向参数输入了一个NumPy数组。函数的内部实现比较简单,先计算NumPy数组中各个元素的平方,再求它们的和(np.sum(x**2)也可以实现同样的处理)。我们来画一下这个函数的图像。结果如图4-8所示,是一个三维图像。

现在我们来求式(4.6)的导数。这里需要注意的是,式(4.6)有两个变量,所以有必要区分对哪个变量求导数,即对x0和x1两个变量中的哪一个求导数。另外,我们把这里讨论的有多个变量的函数的导数称为偏导数。用数学式表示的话,可以写成
![]()
怎么求偏导数呢?我们先试着解一下下面两个关于偏导数的问题。
问题1:求x0 = 3, x1 = 4时,关于x0的偏导数
![]()
![]()
![]()

问题2:求x0 = 3, x1 = 4时,关于x1的偏导数
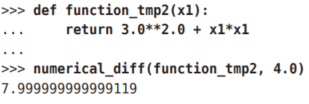
在这些问题中,我们定义了一个只有一个变量的函数,并对这个函数进行了求导。例如,问题1中,我们定义了一个固定x1 = 4的新函数,然后对只有变量x0的函数应用了求数值微分的函数。从上面的计算结果可知,问题1的答案是6.00000000000378,问题2的答案是7.999999999999119,和解析解的导数基本一致。
像这样,偏导数和单变量的导数一样,都是求某个地方的斜率。不过,偏导数需要将多个变量中的某一个变量定为目标变量,并将其他变量固定为某个值。
在上例的代码中,为了将目标变量以外的变量固定到某些特定的值上,我们定义了新函数。然后,对新定义的函数应用了之前的求数值微分的函数,得到偏导数。
















)


