hello大家好，今天是2025年8月23日，我要来给大家分享的是一个高阶数据结构---ST表。

一：引入

1.RMQ问题：

对于一个长度为 n 的序列，有 m 次查询操作，每次查询为一个区间 [l，r] 的最大值（最小值）。

上述问题可以用线段树来解决。但是杀鸡焉用宰牛刀，对于这种静态问题，我们可以使用代码量更少的方式来解决------ST表。

2.ST表：

ST表（Sparse Table，稀疏表）是一种基于动态规划和倍增思想实现的数据结构，形式上是一张二维表格。ST表通过预处理一些信息，从而快速处理区间查询。（类似前缀和数组~）其中，预处理的时间复杂度为 O（n * log n），查询操作为 O（1）。由于在查询前需要预处理出一些信息，因此ST表基本上只能解决静态问题。

**ST表**

将信息预处理完毕之后，对于查询操作只需要在这张二维表格中拿值就可以了。

这里解释一个名词：静态问题---以数组操作为例：

有静态问题就会有动态问题，静态问题就是只有查询操作没有修改操作，或者查询操作是在所有修改操作全部结束之后进行。相比之下，动态问题就是修改操作和查询操作交叉进行。

ST表能够解决的问题（静态问题）线段树绝大多数都可以解决，线段树能解决的问题（静态问题 & 动态问题）ST表就不一定可以解决。

3.ST表维护的信息：

ST表维护的信息需要满足结合律和可重复贡献。（例如区间最值以及区间gcd）

这里借助一张图解释一下什么是结合律和可重复贡献。

如果不满足结合率和可重复贡献，ST表就不能解决。例如区间和以及区间乘积。

二：ST表的实现

计算机中的 log 默认是下取整的，在这里提前说一下，下面就不过多赘述了。

1.ST表维护信息的方式：

对于一个长度为 n 的序列，有 m 次查询操作，每次查询为一个区间 [l，r] 的最大值。

由于区间最值不满足可差性，因此不能像前缀和数组一样搞一张一维表格来预处理某些区间的信息。由于二维表格可以直接用来表示区间，那么可以尝试用二维的表格来预处理，一种直接的方式就是：f[i][j] 表示区间 [i, j] 的最值。

这种方式肯定是可以解决问题的。但是，RMQ 问题的数组一般都是 1e5~1e6 级别的长度，这张二维表格根本无法创建出来（空间溢出）。

我们尝试使用倍增的思想 $2^{j} = 2^{j - 1} + 2 ^ {j - 1}$ 优化一下状态表示:

f[i][j] 表示：从 i 位置开始，长度为 $2^j$ 的区间中，所有元素的最值。

以数组 a = 【5，2，4，6，1，7，5，0，9，3】为例，我们会用下述方式维护区间最大值信息。

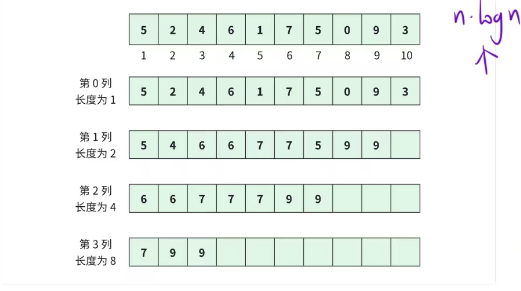
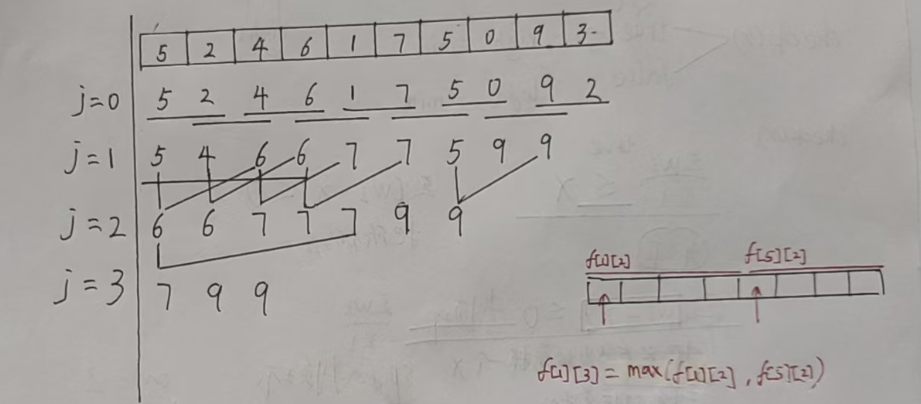
这就是稀疏表的由来，并不是把所有的区间信息存下来，只存长度为 2^j 的区间信息。

优化之后，第二维空间大小 n 只需保证 2^n >= N 就行。25~30就足够了。可见，这个优化是非常有效的。

2.ST表的查询

预处理工作结束之后，我们能否使用预处理出的信息快速查询区间最值呢？

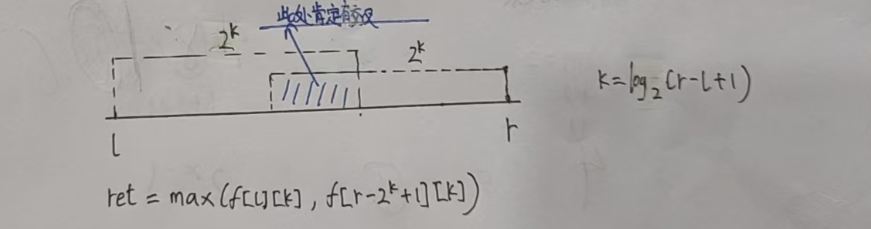
比如，我们要查询区间【l，r】的最大值：

根据状态表示，我们只需要先求出 k = log(2)(r - l + 1)（下取整），然后再从 f[l][k] 和

f[r - (1 << k) + 1][k] 两个格子中取最大值即可。

3.记忆区间起点和区间终点的技巧

起点 + 区间长度 = 下一个区间的起点。
终点 - 区间长度 = 上一个区间的终点。

4.ST表的实现

初始化

#include <iostream>
#include <cmath>using namespace std;
const int N = 1e5 + 10;int n;
int a[N], f[N][25]; // j ^ 25 >= N 就行  void init()
{for(int i = 1; i <= n; i++) f[i][0] = a[i];for(int j = 1; j <= log2(n); j++)for(int i = 1; i + (1 << j) - 1 <= n; i++)f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
}

查询

int query(int l, int r)
{int k = log2(r - l + 1);return max(f[l][k], f[r - (1 << k) + 1][k]);
}

5.优化log（看题目情况）

如果查询次数过多，是会有一个 log 的开销的。如果把 log1~logn 全部预处理出来，那么查询操作的 k 就可以在 O（1）的时间得到。

对于对数运算，有如下公式：

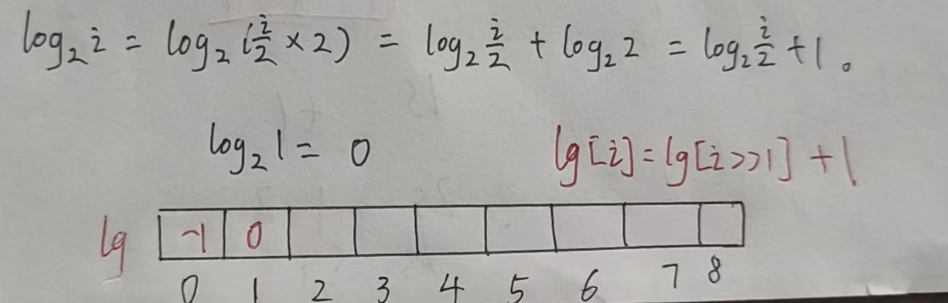
因此可以通过递推，预处理出来所有的 log1 ~ logn。

加了优化的ST表：

#include <iostream>
#include <cmath>using namespace std;
const int N = 1e5 + 10;int n;
int a[N], f[N][25]; // j ^ 25 >= N 就行  
int lg[N];void init()
{lg[0] = -1; // 为了方便递推 lg[1] = lg[0] + 1 == 0 for(int i = 1; i <= n; i++){lg[i] = lg[i >> 1] + 1;f[i][0] = a[i];} for(int j = 1; j <= lg[n]; j++)for(int i = 1; i + (1 << j) - 1 <= n; i++)f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
}int query(int l, int r)
{int k = lg[r - l + 1];return max(f[l][k], f[r - (1 << k) + 1][k]);
}

三：ST表模板题

题目一：【模板】ST表 && RMQ 问题

题目链接：【模板】ST表 && RMQ 问题

#include <iostream>
#include <cmath>using namespace std;const int N = 1e5 + 10;int n, m;
int f[N][25];int RMQ(int l, int r)
{int k = log2(r - l + 1);return max(f[l][k], f[r - (1 << k) + 1][k]);
}int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++) scanf("%d", &f[i][0]);//初始化for (int j = 1; j <= log2(n); j++){for (int i = 1; i + (1 << j) - 1 <= n; i++){f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);}}while (m--){int l, r; scanf("%d%d", &l, &r);printf("%d\n", RMQ(l, r));}return 0;
}

题目二：gcd 区间

题目链接：gcd 区间

#include <iostream>
#include <cmath>using namespace std;const int N = 1e3 + 10;int n, m;
int f[N][25];int gcd(int a, int b)
{return b == 0 ? a : gcd(b, a % b);
}int query(int l, int r)
{int k = log2(r - l + 1);return gcd(f[l][k], f[r - (1 << k) + 1][k]);
}int main()
{cin >> n >> m;for (int i = 1; i <= n; i++) cin >> f[i][0];for (int j = 1; j <= log2(n); j++){for (int i = 1; i + (1 << j) - 1 <= n; i++){f[i][j] = gcd(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);}}while (m--){int l, r; cin >> l >> r;cout << query(l, r) << endl;}return 0;
}

四：ST表练习题

题目一：质量检测

题目链接：质量检测

这道题目的最优解是单调队列 O（n），但是我们这个专题是 ST 表，因此给出ST表的解法，下去之后也要尝试一下使用单调队列解决这道问题。

#include <iostream>
#include <cmath>
#include <cstring>using namespace std;const int N = 1e5 + 10;int n, m;
int f[N][25];int query(int l, int r)
{int k = log2(r - l + 1);return min(f[l][k], f[r - (1 << k) + 1][k]);
}int main()
{memset(f, 0x3f, sizeof f);cin >> n >> m;for (int i = 1; i <= n; i++) cin >> f[i][0];for (int j = 1; j <= log2(n); j++){for (int i = 1; i + (1 << j) - 1 <= n; i++){f[i][j] = min(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);}}for (int i = 1; i + m - 1 <= n; i++){cout << query(i, i + m - 1) << endl;}return 0;
}

题目二：Balanced Lineup G

题目链接：Balanced Lineup G

#include <iostream>
#include <cstring>
#include <cmath>using namespace std;const int N = 5e4 + 10;int n, m;
int f[N][28];
int g[N][28];int query(int l, int r)
{int k = log2(r - l + 1);return max(f[l][k], f[r - (1 << k) + 1][k])- min(g[l][k], g[r - (1 << k) + 1][k]);
}int main()
{cin >> n >> m;memset(g, 0x3f, sizeof g);for (int i = 1; i <= n; i++){cin >> f[i][0];g[i][0] = f[i][0];}for (int j = 1; j <= log2(n); j++){for (int i = 1; i + (1 << j) - 1 <= n; i++){f[i][j] = max(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);g[i][j] = min(g[i][j - 1], g[i + (1 << (j - 1))][j - 1]);}}while (m--){int l, r; cin >> l >> r;cout << query(l, r) << endl;}return 0;
}

今天的分享就到这里了~~，如果大家有疑问的话，欢迎下来之后和我沟通~~