1.普利姆(Prim)算法

1.1Prim算法定义

Prim算法在找最小生成树的时候，将顶点分为两类，一类是在查找的过程中已经包含在生成树中的顶点(假设为A类)，剩下的另一类为B类。

对于给定的连通图，起始状态全部顶点都为B类。在找最小生成树时，选定任意一个顶点作为起始点，并将之从B类移至A类；然后找出B类中到A类中的顶点之间权值最小的顶点，将之从B类移至A类，如此重复，直到B类中没有顶点为止。所走过的顶点和边就是该连通图的最小生成树。(简单对比一下：上一节课的Kruskal是找边，这几棵的Prim算法是找顶点。)

1.2Prim算法逻辑

动态维护一个所有待激活的顶点数组，从图中任意选取一个顶点激活它，激活了后就能发现新的边，找到权值数组里最小的边，激活另外一个顶点，更新权值数组，再来找权值数组里最小的边，激活另外的顶点，以此重复，直到所有顶点都激活。

如图1我们先激活A，激活后发现新的边，更新权值数组里的值，A连着B,F,G，所以很明显我们需要更新B,F,G下的权值，其他没有直接连接的我们暂时认为权值无穷大，找到权值数组里面最小的边是AB这条，激活B顶点，发现新的边，更新权值数组里的边，B连着A,F,C，由于A和B已激活，我们看需不需要更新F和C下的权值，发现B到F的这条边的权值是7<16,我们更新F下的权值为7，C下的权值为10，激活F顶点。

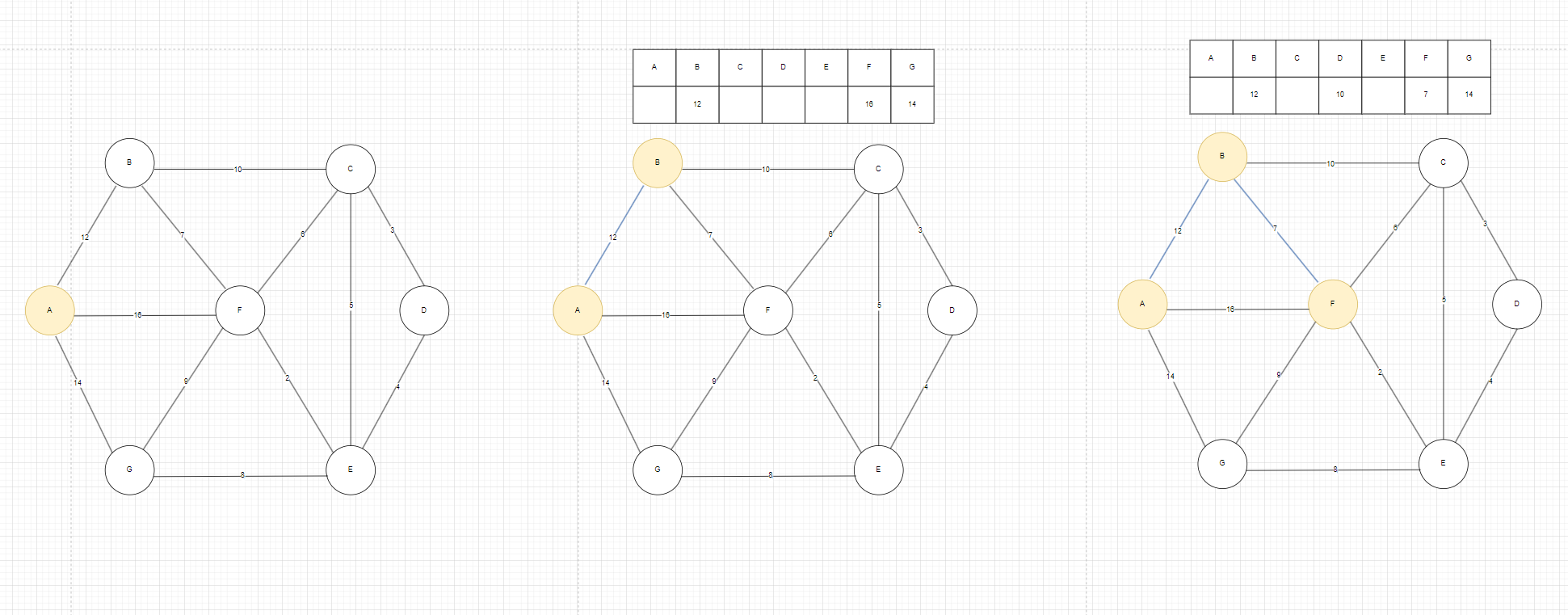
图1

以此重复这个过程，最终结果如图2，在找到C之后，就只有G没有激活了，G的有三条边，选取最小的那条边8作为权值数组里面的值。

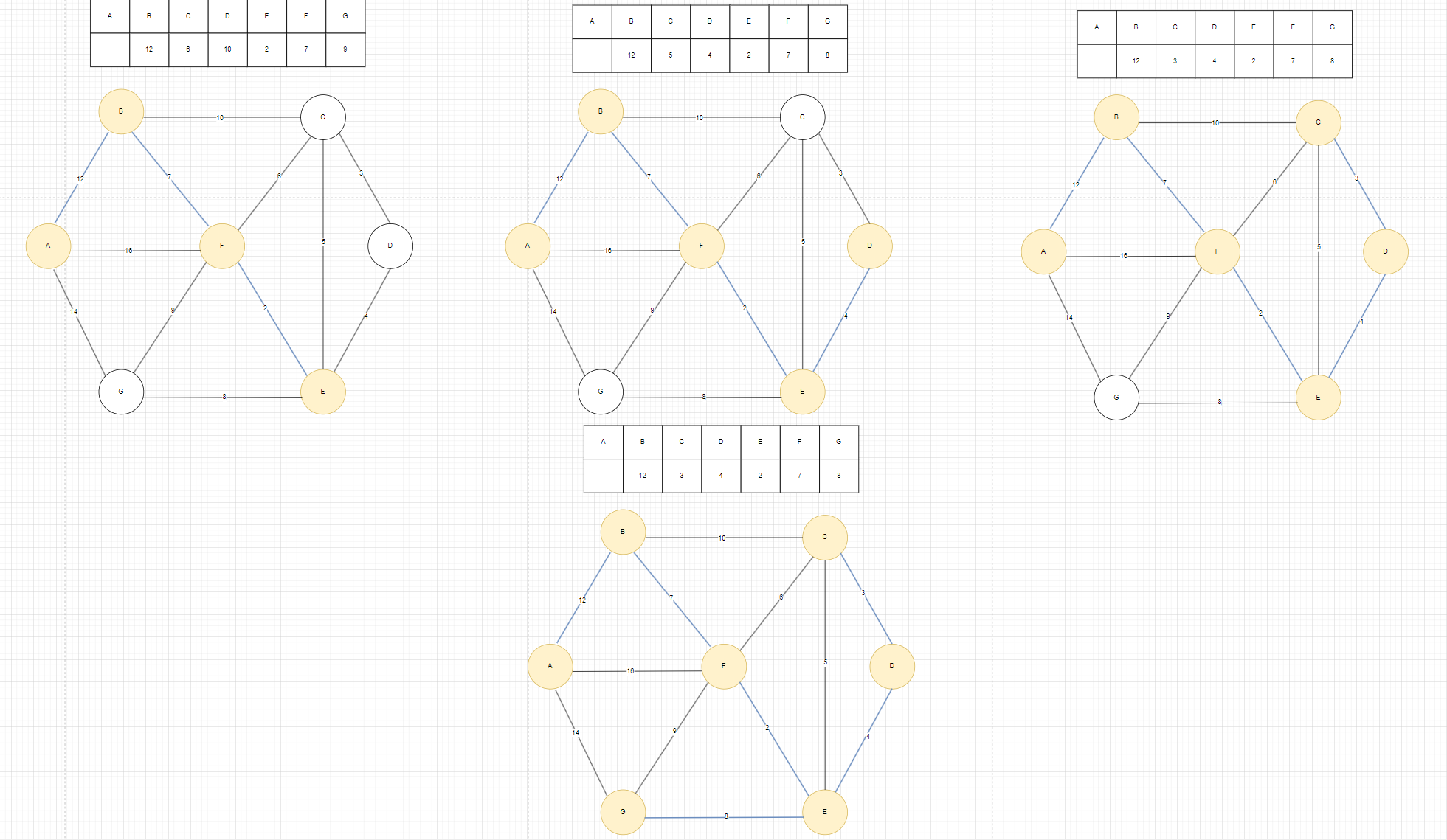图2

如图3，注意在这里Kruskal算法和Prim算法最后构成的最小生成树一样，但在实际过程中，这两种算法构建出来的最小生成树可能不一样。

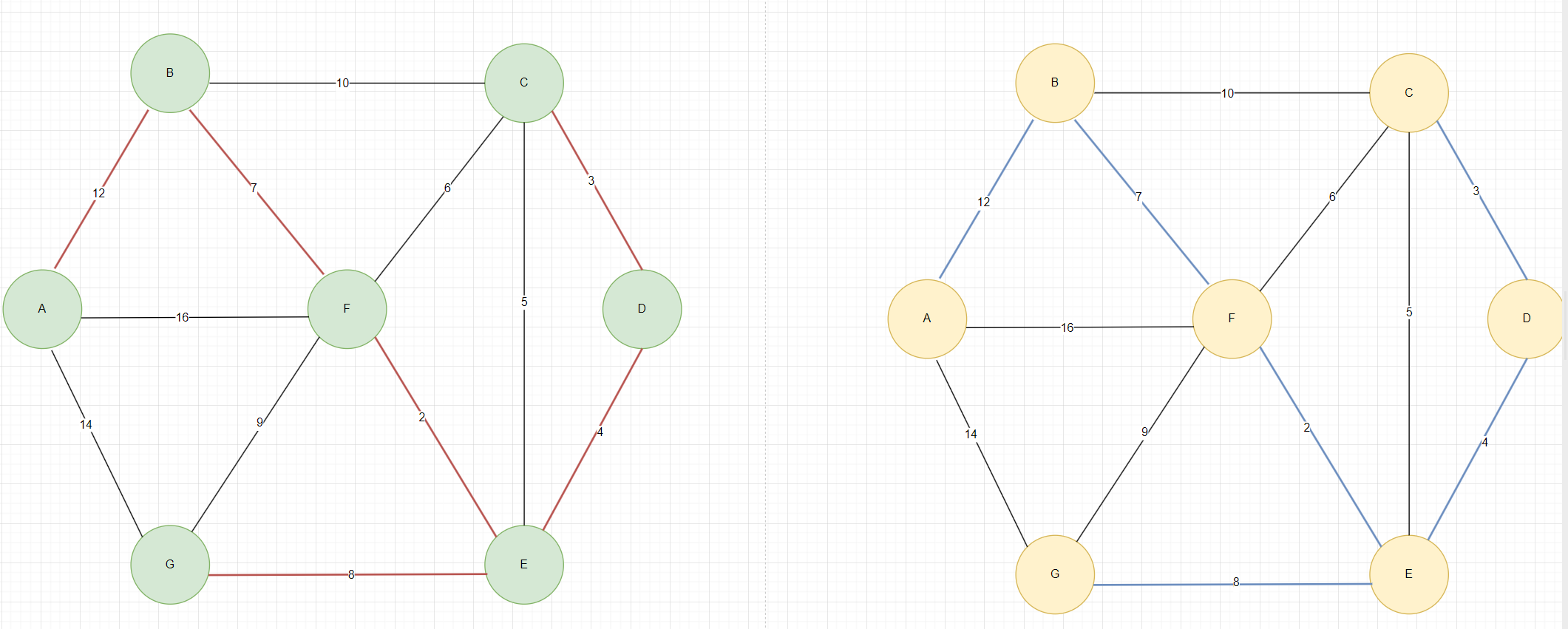
图3

1.3Prim代码分析

如图4我们定义一个cost数组，里面存的是权值数组，初始时，每个边都是INF(无穷大)，一个visited数组存已经被激活的点,由于我不想只打印出最后的权值大小，我还想打印打出对应选取了哪些边在最小生成树中，初始化时全部设为-1，意味着没有激活前，没有其他的顶点到自己。

第一次激活A点，A连着有三条边，分别对应的顶点是B,F,G,在cost中A激活那一行填写对应的权值，在该行中找到最小的权值，标黄，cost标了黄色的格子意味着是当前一行权值数组中最小的边，激活它，后面在更新权值数组的时候就可以不用管黄色的那一列了。在visited数组中，由于A的激活，我们发现三条边对应的是B,F,G，说明A能到B,F,G我们就在A激活那一行中填写A到了这三个顶点，但我们一次只能确定一个谁可以被保留，因为我们在costA激活的那一行中，一次只能找到一个最小权值，有的同学可能会问，为什么要把visited中A激活那一行F和G下的A也暂时保留呢，由上1.2分析得后面B是要连F得，但如果连接BF的那条边很大，比连接AF下的边大，那么我们就不是B到F，而是A到F，如果不保留的话就找不到了。由于我们激活的是B，又开始对B执行上述逻辑操作，一直到所有顶点被激活。

visited中A激活那里B列下的A要标黄，意味着确定了最小生成树中其中某一条边的顶点是这两个

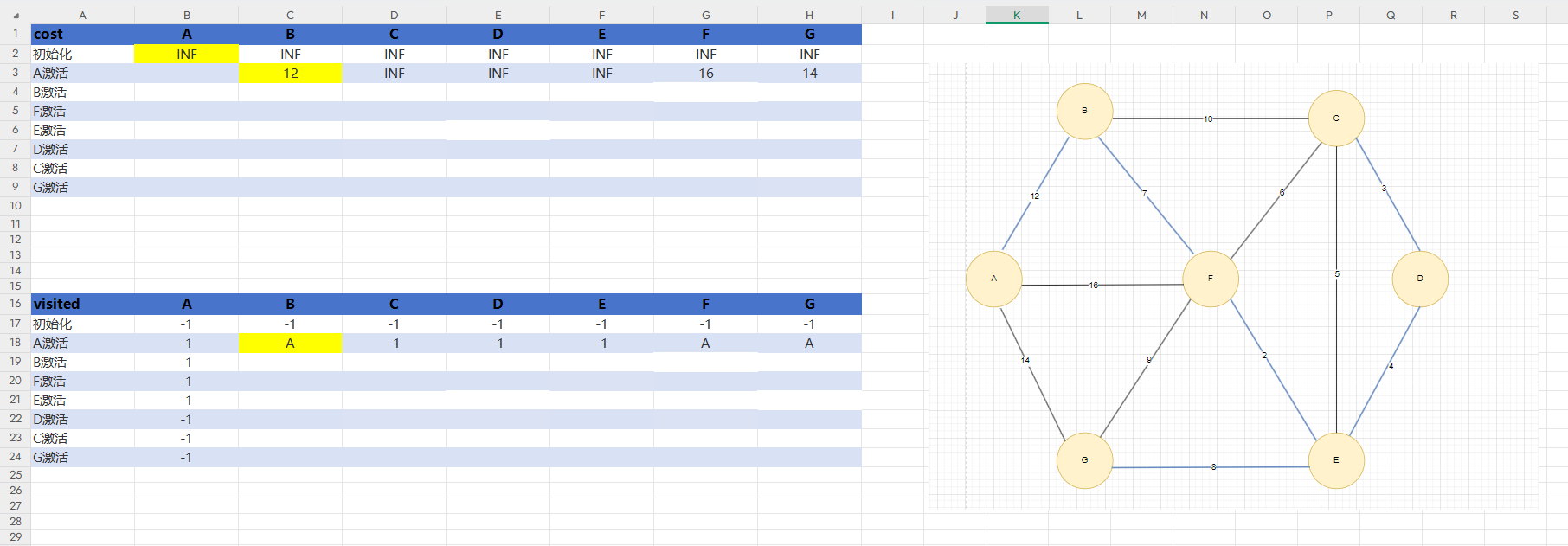
图4

过程和结果如图5：

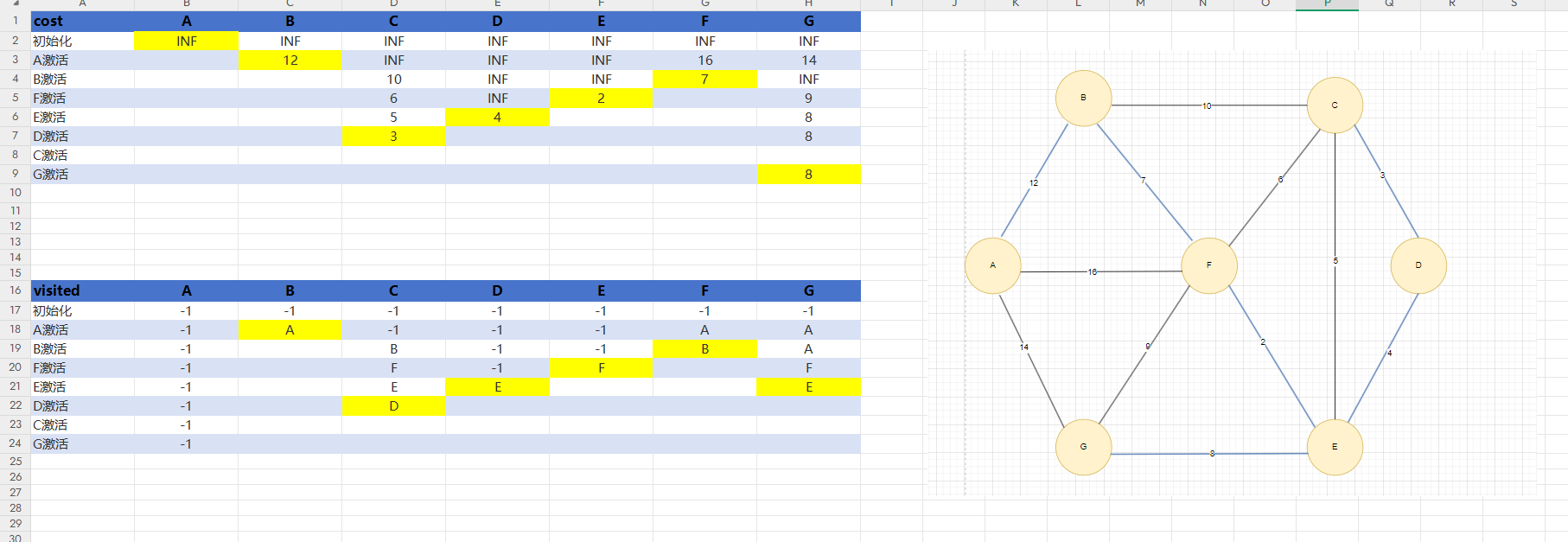
图5

注意实际代码实现的时候并不是二维数组，而是意味数组，我这里画成二维数组只是方便看过程。

2.Prim算法代码实现

先来看测试的接口：

void setupMGraph(MatrixGraph *graph, int edgeValue) {//				  0    1    2    3    4    5   6char *names[] = {"A", "B", "C", "D", "E", "F", "G"};initMatrixGraph(graph, names, sizeof(names)/sizeof(names[0]), 0, edgeValue);addMGraphEdge(graph, 0, 1, 12);addMGraphEdge(graph, 0, 5, 16);addMGraphEdge(graph, 0, 6, 14);addMGraphEdge(graph, 1, 2, 10);addMGraphEdge(graph, 1, 5, 7);addMGraphEdge(graph, 2, 3, 3);addMGraphEdge(graph, 2, 4, 5);addMGraphEdge(graph, 2, 5, 6);addMGraphEdge(graph, 3, 4, 4);addMGraphEdge(graph, 4, 5, 2);addMGraphEdge(graph, 4, 6, 8);addMGraphEdge(graph, 5, 6, 9);
}void test02() {MatrixGraph graph;EdgeSet *result;int sumWeight = 0;setupMGraph(&graph, INF);result = malloc(sizeof(EdgeSet) * (graph.edgeNum - 1));if (result == NULL) {return;}sumWeight = PrimMGraph(&graph, 0, result);printf("sumWeight = %d\n", sumWeight);for (int i = 0; i < graph.nodeNum - 1; ++i) {printf("edge %d: <%s> ---- <%d> ---- <%s>\n", i + 1,graph.vex[result[i].begin].show, result[i].weight,graph.vex[result[i].end].show);}
}

我们在void setupMGraph(MatrixGraph *graph, int edgeValue)中没有相连的两个顶点之间的权值赋为INF，相连的两个顶点间赋值相应的权值，在void test02()中用PrimMGraph(&graph, 0, result);得到权值总和并随后打印出边和顶点的信息

Prim算法核心:int PrimMGraph(const MatrixGraph* graph, int startV, EdgeSet* result);

/* graph: 表示指向邻接矩阵的图结构* startV:表示激活的第一个顶点坐标* result:表示最小生成树的边的激活情况*/
int PrimMGraph(const MatrixGraph* graph, int startV, EdgeSet* result) {int *cost = malloc(sizeof(int) * graph->nodeNum);			// 图中各顶点的权值数组int *mark = malloc(sizeof(int) * graph->nodeNum);			// 图中顶点激活的状态int *visited = malloc(sizeof(int) * graph->nodeNum);		// 从哪个顶点开始访问，-1表示没有被访问到int sum = 0;// 1. 更新第一个节点激活的状态for (int i = 0; i < graph->nodeNum; i++) {cost[i] = graph->edges[startV][i];mark[i] = 0;// 1.1 更新visit信息，从哪个节点可以访问if (cost[i] < INF) {visited[i] = startV;} else {visited[i] = -1;}}mark[startV] = 1;int k = 0;// 2. 动态激活节点，找最小值for (int i = 0; i < graph->nodeNum - 1; ++i) {// 找未加入树且cost最小的顶点kint min = INF;k = 0;for (int j = 0; j < graph->nodeNum; ++j) {if (mark[j] == 0 && cost[j] < min) {min = cost[j];k = j;}}// 将k加入树，记录边信息mark[k] = 1;result[i].begin = visited[k];result[i].end = k;result[i].weight = min;sum += min;// 每激活一个顶点，需要更新cost数组for (int j = 0; j < graph->nodeNum; ++j) {if (mark[j] == 0 && graph->edges[k][j] < cost[j]) {cost[j] = graph->edges[k][j];visited[j] = k;}}}free(cost);free(mark);free(visited);return sum;
}

我们需要申请三个空间分别用来存图中各顶点的权值数组，图中顶点激活的状态和对应带权边的两个顶点信息。

先来看1.更新第一个节点激活的状态，在cost里面存放激活的第一个顶点与图中其他顶点间的边的权值大小，并默认所有顶点还未被访问，然后更新visited数组中的信息，如果cost里面存的权值大小小于INF，则把对应visited数组下的值填成starV，说明两个顶点之间有边，否则就认为starV顶点与其无边，在对应visited数组下设为-1，初始化完我们认为starV已被访问：mark[startV] = 1;此时三个数组如图6：

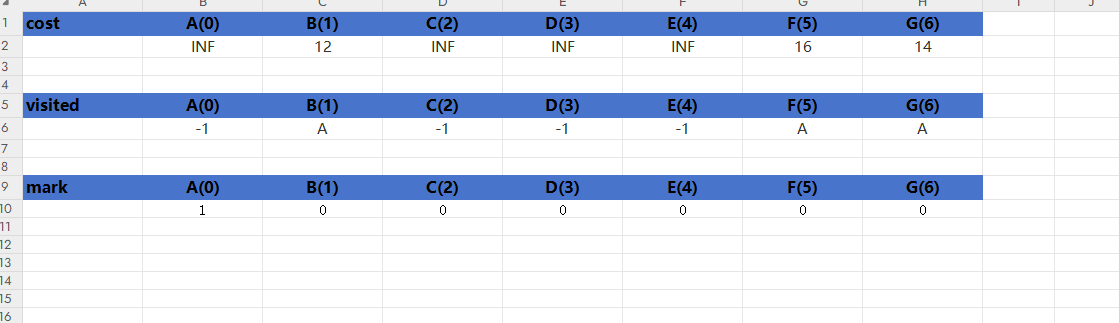
图6

定义一个k标记待加入的顶点：
在每次循环中，程序会遍历所有未加入生成树的顶点（mark[j] == 0），找到 cost[j] 最小的顶点，并用 k 记录该顶点的索引。这个顶点 k 就是本次要加入生成树的顶点。
作为新顶点更新后续状态：
当 k 被标记为 “已加入生成树”（mark[k] = 1）后，程序会以 k 为新的起点，更新其他未加入顶点的 cost 和 visited 数组。此时 k 成为 “已生成树” 的一部分，用于后续计算其他顶点与树的最小连接边权。

来看2，先定义一个最小值，这个最小值存的是INF，这样比这个最小值小就可以加入cost里了，找未加入树且cost最小的顶点k，找到过后将k加入树，记录边信息并把k加入mark标记中说明已被访问。每次激活一个顶点，需要更新cost里面的权值当然更新的时候只更新没有访问过的顶点，因为已被访问过的顶点已经被我们纳入了最小生成树中，即我们不需要更新图4，图5中cost和visited里面标黄的部分。循环 graph->nodeNum - 1次，因为先前已经加入了starV顶点，初始时有 1 个顶点，循环 graph->nodeNum - 1 次后，新增 graph->nodeNum - 1 个顶点，总共加入的顶点数为graph->nodeNum个。

最后测一下：

#include <stdio.h>
#include <stdlib.h>
#include "Kruskal.h"
#include "Prim.h"void setupMGraph(MatrixGraph *graph, int edgeValue) {//				  0    1    2    3    4    5   6char *names[] = {"A", "B", "C", "D", "E", "F", "G"};initMatrixGraph(graph, names, sizeof(names)/sizeof(names[0]), 0, edgeValue);addMGraphEdge(graph, 0, 1, 12);addMGraphEdge(graph, 0, 5, 16);addMGraphEdge(graph, 0, 6, 14);addMGraphEdge(graph, 1, 2, 10);addMGraphEdge(graph, 1, 5, 7);addMGraphEdge(graph, 2, 3, 3);addMGraphEdge(graph, 2, 4, 5);addMGraphEdge(graph, 2, 5, 6);addMGraphEdge(graph, 3, 4, 4);addMGraphEdge(graph, 4, 5, 2);addMGraphEdge(graph, 4, 6, 8);addMGraphEdge(graph, 5, 6, 9);
}void test02() {MatrixGraph graph;EdgeSet *result;int sumWeight = 0;setupMGraph(&graph, INF);result = malloc(sizeof(EdgeSet) * (graph.edgeNum - 1));if (result == NULL) {return;}sumWeight = PrimMGraph(&graph, 0, result);printf("sumWeight = %d\n", sumWeight);for (int i = 0; i < graph.nodeNum - 1; ++i) {printf("edge %d: <%s> ---- <%d> ---- <%s>\n", i + 1,graph.vex[result[i].begin].show, result[i].weight,graph.vex[result[i].end].show);}
}int main() {test02();return 0;
}

结果：

D:\work\DataStruct\cmake-build-debug\03_GraphStruct\MiniTree.exe
sumWeight = 36
edge 1: <A> ---- <12> ---- <B>
edge 2: <B> ---- <7> ---- <F>
edge 3: <F> ---- <2> ---- <E>
edge 4: <E> ---- <4> ---- <D>
edge 5: <D> ---- <3> ---- <C>
edge 6: <E> ---- <8> ---- <G>进程已结束，退出代码为 0