一、实验目的
实验目标
构建基于神经网络模型的数据分析与模式识别框架,探明神经网络在大数据分析中的意义。
实验任务
构建基于深度 BP 神经网络与卷积神经网络的数据分析与模式识别框架,将数据集 MNIST 与 CIFAR-10 分别在两种模型中训练,并比较测试效果。
使用数据集
MNIST 数据集
CIFAR-10 数据集
二、实验原理
阶段一分析:
分析问题需求,明确分类任务目标
在本阶段,我们的目标是构建一个图像分类系统,能够将输入图像准确分类到对应的类别。首先,搭建数据读取与预处理模块,需要调用MNIST和CIFAR-10两个标准图像数据集作为实验数据。然后,搭建数据与模型接口,为以后将这两个数据集放入模型中做好准备。接下来,实现模型评估模块,按照老师所讲的,计算分类评估指标错误率与精确度,最后在可视化中搭建roc曲线。
阶段二分析(BP神经网络):
BP (Back Propagation)神经网络也是前馈神经网络,只是它的参数权重值是由反向传播学习算法进行调整的
BP 神经网络模型拓扑结构包括输入层、隐层和输出层,利用激活函数来实现从输入到输出的任意非线性映射,从而模拟各层神经元之间的交互
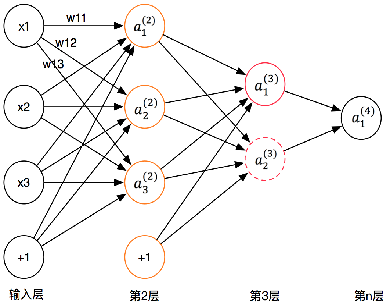
基本步骤:初始化网络权值和神经元的阈值,一般通过随机的方式进行初始化前向传播: 计算隐层神经元和输出层神经元的输出后向传播: 根据目标函数公式修正权值。
BP 神经网络的核心思想是由后层误差推导前层误差,一层一层的反传,最终获得各层的误差估计,从而得到参数的权重值。由于权值参数的运算量过大,一般采用梯度下降法来实现
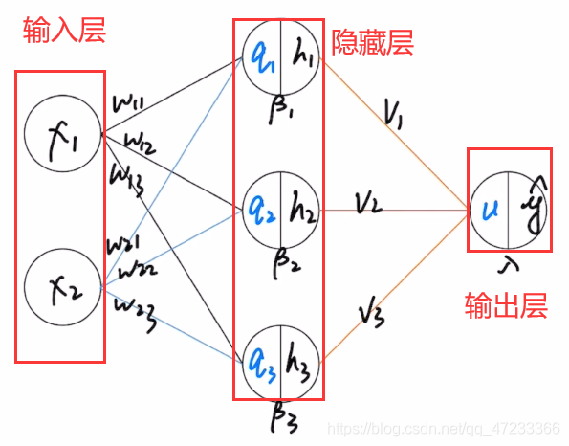

输入层是神经网络的起点,其作用是将外部数据输入模型。在图像分类任务中,图像需要先被展平为一维向量(如 MNIST 的 28x28 图像被展平为 784 维向量),并作为输入层的节点传入网络。输入层本身不做任何计算,只负责数据的传递。
神经网络隐藏层
隐藏层是网络中最核心的部分,用于提取特征与学习数据之间的非线性关系。每个隐藏层由多个神经元(节点)构成,节点之间通过权重连接。每个神经元会对其输入做一次线性加权求和,再通过激活函数进行非线性变换(如 ReLU、Sigmoid、Tanh 等),提高模型的拟合与表达能力。多个隐藏层串联构成了“深度”网络。
神经网络输出层
输出层的作用是将模型内部的高维特征最终映射为分类结果。对于多分类任务(如本实验中的 MNIST 和 CIFAR-10,均为 10 类),输出层一般设置为一个Linear全连接层,输出维度为类别数(10),并通过Softmax 函数 转换为概率形式,用于分类决策。
阶段三分析(CNN神经网络)
卷积神经网络是人工神经网络的一种,由对猫的视觉皮层的研究发展而来,视觉皮层细胞对视觉子空间更敏感,通过子空间的平铺扫描实现对整个视觉空间的感知。
卷积神经网络目前是深度学习领域的热点,尤其是图像识别和模式分类方面,优势在于具有共享权值的网络结构和局部感知(也称为稀疏连接)的特点,能够降低神经网络的运算复杂度。
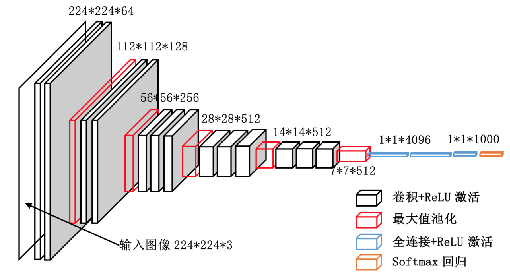
卷积层和子采样层是特征提取功能的核心模块,卷积神经网络的低层由卷积层和子采样层交替组成,在保持特征不变的情况下减少维度空间和计算时间,更高层次是全连接层,输入是由卷积层和子采样层提取到的特征,最后一层是输出层,可以是一个分类器,采用逻辑回归、Softmax回归、支持向量机等进行模式分类,也可以直接输出某一结果。
卷积层
通过卷积层的运算,可以将输入信号在某一特征上加强,从而实现特征的提取,也可以排除干扰因素,从而降低特征的噪声。卷积操作是指将一个可移动的小窗口(称为数据窗口)与图像进行逐元素相乘然后相加的操作。这个小窗口其实是一组固定的权重,它可以被看作是一个特定的滤波器(filter)或卷积核。
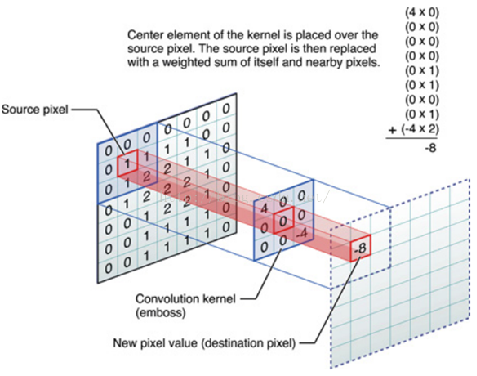
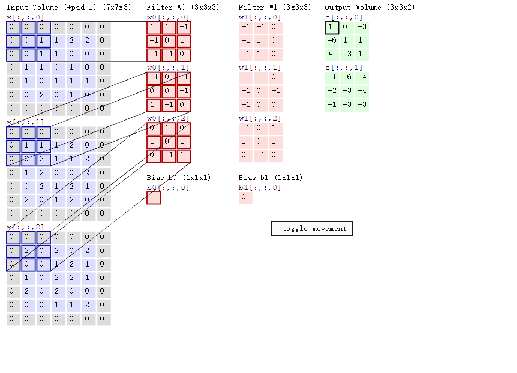
池化层
池化层是一种向下采样的形式,在神经网络中也称之为子采样层。一般使用最大池化将特征区域中的最大值作为新的抽象区域的值,减少数据的空间大小。参数数量和运算量也会减少,减少全连接的数量和复杂度,一定程度上可以避免过拟合。池化的结果是特征减少、参数减少。
全连接层
卷积层得到的每张特征图表示输入信号的一种特征,而它的层数越高表示这一特征越抽象,为了综合低层的每个卷积层特征,用全连接层将这些特征结合到一起,然后用Softmax进行分类或逻辑回归分析。
三、实验代码
3.1 构建数据分析与模式识别框架(第四周)
搭建数据读取与预处理模块(支持 MNIST / CIFAR-10)
数据读取与预处理部分主要功能是根据用户选择加载 MNIST 或 CIFAR-10 数据集。
主要思路:使用torchvision.datasets 提供的接口自动下载并加载数据,同时通过 transforms 对图像进行预处理,包括将图像转换为张量 (ToTensor) 并进行标准化(使像素值服从指定均值和标准差的分布),从而提升模型训练的效果与稳定性。
最终返回处理后的训练集,并输出图像数量和尺寸信息,便于后续模型训练使用。
ps:使用 K-Fold 方法分解数据集(k=5)放在了另一模块,分解后会直接训练
def load_dataset(use_mnist=True):if use_mnist:transform = transforms.Compose([transforms.ToTensor(),transforms.Normalize((0.1307,), (0.3081,))])dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)else:transform = transforms.Compose([transforms.ToTensor(),transforms.Normalize((0.5,), (0.5,))])dataset = datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)print(f"加载数据集完成:{len(dataset)}张图像,尺寸为 {dataset[0][0].shape}")return dataset搭建数据与模型接口模块
这一模块作为数据与模型的接口,核心目的是根据用户选择动态构建不同类型的神经网络模型。
函数 get_model 接收模型类型(bp 或 cnn)和输入数据的形状等参数:当选择 bp 时,将图像展平成一维向量传入多层感知机 DeepBPNet;当选择 cnn 时,保留图像的通道信息并构建卷积神经网络 CustomCNN。
同时通过 **kwargs 支持对网络结构参数(如初始化方式、层数等)进行灵活配置。该接口实现了模型结构的统一调用,便于后续训练与评估过程的模块化管理。
# ========== 数据与模型接口 ==========
def get_model(model_type='bp', input_shape=(1, 28, 28), num_classes=10, **kwargs):if model_type == 'bp':input_size = np.prod(input_shape)return DeepBPNet(input_size=input_size, num_classes=num_classes, **kwargs)elif model_type == 'cnn':return CustomCNN(in_channels=input_shape[0], num_classes=num_classes, **kwargs)else:raise ValueError("模型必须是'bp'或者'cnn'")搭建模型评估模块
这一模块是整个实验的核心部分——模型评估模块。
其主要功能是在训练过程中使用 K-Fold 交叉验证 方法(本实验设定 k=5),将原始数据划分为训练集和验证集。
在每一折中,首先利用用户指定的模型类型(CNN 或 BP)通过 get_model 动态构建模型,并进行若干轮次的训练。
接着,在验证集中进行推理,计算预测结果与真实标签的准确率(Accuracy)与对数损失(Log Loss)。每折的结果都会记录并输出,
最终返回所有折次的评估指标和分类概率,为模型表现对比与后续可视化分析提供基础。
# ========== 模型评估模块 ==========
def evaluate_model_kfold(dataset, model_type='cnn', k_folds=5, batch_size=64, num_classes=10, device=None, epochs=1, **kwargs):if device is None:device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
indices = list(range(len(dataset)))kf = KFold(n_splits=k_folds, shuffle=True, random_state=42)
all_fold_metrics = []all_probs = []all_targets = []
for fold, (train_idx, val_idx) in enumerate(kf.split(indices)):print(f"\n 训练轮数 {fold + 1}/{k_folds}")
train_subset = Subset(dataset, train_idx)val_subset = Subset(dataset, val_idx)train_loader = DataLoader(train_subset, batch_size=batch_size, shuffle=True)val_loader = DataLoader(val_subset, batch_size=batch_size, shuffle=False)
sample_input, _ = next(iter(train_loader))model = get_model(model_type=model_type,input_shape=sample_input.shape[1:],num_classes=num_classes,**kwargs).to(device)
criterion = nn.CrossEntropyLoss()optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
# === 训练阶段 ===model.train()for epoch in range(epochs):for inputs, labels in train_loader:inputs, labels = inputs.to(device), labels.to(device)optimizer.zero_grad()outputs = model(inputs)loss = criterion(outputs, labels)loss.backward()optimizer.step()
# === 验证阶段 ===model.eval()y_true, y_pred, y_prob = [], [], []
with torch.no_grad():for inputs, labels in val_loader:inputs, labels = inputs.to(device), labels.to(device)outputs = model(inputs)probs = F.softmax(outputs, dim=1)preds = torch.argmax(probs, dim=1)
y_true.extend(labels.cpu().numpy())y_pred.extend(preds.cpu().numpy())y_prob.extend(probs.cpu().numpy())
acc = accuracy_score(y_true, y_pred)loss = log_loss(y_true, y_prob, labels=list(range(num_classes)))
all_fold_metrics.append({'fold': fold + 1, 'accuracy': acc, 'loss': loss})all_probs.extend(y_prob)all_targets.extend(y_true)
print(f" Fold {fold + 1} Accuracy: {acc:.4f}, Loss: {loss:.4f}")
return all_fold_metrics, np.array(all_probs), np.array(all_targets)
搭建模型评估可视化模块
这一模块是模型评估可视化部分,主要功能是绘制多分类任务中的 ROC 曲线,帮助我们直观判断模型对每一类别的区分能力。
首先通过 label_binarize 对目标标签进行 One-Hot 编码,然后计算每个类别的真正率(TPR)与假正率(FPR),并进一步求得每类的 AUC(曲线下面积)作为性能指标。
最终利用 Matplotlib 对每个类别的 ROC 曲线进行绘图,并可选择保存或直接展示。该模块能有效展示模型对不同类别的分类效果,提供辅助判断和模型优化依据。
def plot_multiclass_roc(probs, targets, num_classes, save_path=None):targets_onehot = label_binarize(targets, classes=list(range(num_classes)))
fpr = dict()tpr = dict()roc_auc = dict()
for i in range(num_classes):fpr[i], tpr[i], _ = roc_curve(targets_onehot[:, i], probs[:, i])roc_auc[i] = auc(fpr[i], tpr[i])
plt.figure(figsize=(10, 8))for i in range(num_classes):plt.plot(fpr[i], tpr[i], label=f"Class {i} (AUC = {roc_auc[i]:.2f})")
plt.plot([0, 1], [0, 1], 'k--', label='Random')plt.xlim([0.0, 1.0])plt.ylim([0.95, 1.05])plt.xlabel('假警报率')plt.ylabel('识别率')plt.title('多分类模型的ROC曲线')plt.rcParams['font.sans-serif'] = ['SimHei']plt.legend(loc='lower right')
if save_path:plt.savefig(save_path)print(f" ROC曲线已保存到 {save_path}")else:plt.show()3.2 构建深层神经网络模型(第六周)
构建 10 层 BP 神经网络模型
该BP网络结构包括:
输入层:将图像展平为一维向量,输入维度默认为
784,对应于28×28的灰度图(如 MNIST)。隐藏层:通过参数
num_layers=10指定总层数,其中hidden_size=128表示每层的神经元数量,采用了 8 个中间隐藏层(10 层结构 = 输入层 + 8 个隐藏层 + 输出层),并使用ReLU激活函数进行非线性变换。输出层:将最后一层的输出映射到
num_classes=10,用于10类分类任务。
class DeepBPNet(nn.Module):def __init__(self, input_size=784, hidden_size=128, num_classes=10, num_layers=10, init_method='xavier'):super(DeepBPNet, self).__init__()assert num_layers >= 2, "网络层数必须 >= 2"self.input_layer = nn.Linear(input_size, hidden_size)self.hidden_layers = nn.ModuleList([nn.Linear(hidden_size, hidden_size) for _ in range(num_layers - 2)])self.output_layer = nn.Linear(hidden_size, num_classes)self.init_weights(method=init_method) def forward(self, x):x = x.view(x.size(0), -1)x = F.relu(self.input_layer(x))for layer in self.hidden_layers:x = F.relu(layer(x))x = self.output_layer(x)return x
3.3 构建卷积神经网络模型(第七周)
构建 3 层 CNN 神经网络模型
本模块主要通过构建一个可配置的卷积神经网络(CustomCNN 类)实现图像分类任务,其核心思路是:利用多层卷积层、激活函数和池化操作提取图像特征,随后通过全连接层完成分类预测。
该 CNN 网络结构包括以下部分:
输入层:接收尺寸为
28×28的灰度图像,输入通道默认为1(适用于 MNIST),也支持自定义为彩色图像的3通道(如 CIFAR-10)。卷积模块:通过参数
conv_layers=3控制卷积层数,每层包含一个3×3的卷积核(padding=1保持尺寸)、激活函数(如ReLU、Tanh等)以及2×2的最大池化操作(MaxPool2d),用于特征提取与降维。每一层的通道数由base_channels=16按2^i级数增长,即为16 → 32 → 64。全连接层:卷积模块输出展平后,通过两个线性全连接层处理。第一层映射到
128个神经元,第二层输出num_classes=10,用于多分类任务。激活函数与初始化:激活函数可选(如
ReLU、Sigmoid等),通过参数activation控制;所有卷积层与线性层的权重初始化方式也可配置(如xavier、kaiming等),增强模型灵活性与实验可控性。
class CustomCNN(nn.Module):def __init__(self, in_channels=1, num_classes=10, conv_layers=3, base_channels=16, activation='relu', init_method='xavier'):super(CustomCNN, self).__init__()assert conv_layers >= 1, "至少要有一个卷积层"self.activation_name = activationself.activation_fn = self._get_activation_fn(activation)self.conv_blocks = nn.ModuleList()channels = in_channelsfor i in range(conv_layers):out_channels = base_channels * (2 ** i)self.conv_blocks.append(nn.Sequential(nn.Conv2d(channels, out_channels, kernel_size=3, padding=1),self.activation_fn,nn.MaxPool2d(2, 2)))channels = out_channelsdummy_input = torch.zeros(1, in_channels, 28, 28)with torch.no_grad():for layer in self.conv_blocks:dummy_input = layer(dummy_input)flatten_dim = dummy_input.view(1, -1).shape[1]self.fc1 = nn.Linear(flatten_dim, 128)self.fc2 = nn.Linear(128, num_classes)self.init_weights(init_method) def forward(self, x):for layer in self.conv_blocks:x = layer(x)x = x.view(x.size(0), -1)x = self.activation_fn(self.fc1(x))x = self.fc2(x)return x
四、实验设计
4.1 数据集及数据集划分方式
MNIST 数据集:包含 70,000 张 28×28 像素的灰度手写数字图片,共 10 个类别(0~9)。本实验使用其中的 训练集部分(60,000 张)作为训练与验证数据。
CIFAR-10 数据集:包含 60,000 张 32×32 像素的彩色图像,分为 10 个类别,如飞机、汽车、猫、狗等。实验中使用其中的训练集部分(50,000 张)进行模型训练与评估。
为了更稳定且全面地评估模型性能,本实验采用了K 折交叉验证法(K-Fold Cross Validation)。我们将训练集划分为 5 份(k=5),每次选取其中一份作为验证集,其余部分用于训练,重复 5 次后计算每折的准确率与损失,并求取平均值,减小随机性影响,使结果更具参考价值。
4.2 实验选用的超参数
BP选用的超参数:
初始化方式:Xavier / Kaiming / Normal / Uniform
神经元个数:64、128、256、512
网络层数:3、5、10、20
激活函数:ReLU / LeakyReLU / Sigmoid / Tanh
CNN选用的超参数:
初始化方式:Xavier / Kaiming / Normal / Uniform
卷积核个数:8、16、32、64
卷积层数:1、2、3、4
激活函数:ReLU / LeakyReLU / Sigmoid / Tanh
五、实验结果展示与分析
5.1 对比图表
BPNet vs CNN 性能对比(进行完优化的对比图表)
| 模型类型 | 数据集 | 最佳准确率 | 最低损失 | 最优配置简述 |
|---|---|---|---|---|
| BPNet | MNIST | 0.9575 | 0.1391 | Xavier 128 3 ReLU |
| BPNet | CIFAR-10 | 0.4389 | 1.5870 | Xavier 128 3 ReLU |
| CNN | MNIST | 0.9853 | 0.0474 | Xavier 64 3 LeakyReLU |
| CNN | CIFAR-10 | 0.5647 | 1.2114 | Kaiming 64 3 tanh |
5.2 改变模型超参数
BP更换不同模块参数以探明作用:
初始化方式:Xavier / Kaiming / Normal / Uniform
神经元个数:64、128、256、512
网络层数:3、5、10、20
激活函数:ReLU / LeakyReLU / Sigmoid / Tanh
MINST
为了探究网络结构各项参数对模型性能的影响,我们在MNIST数据集上通过更改初始化方式、神经元个数、网络层数和激活函数,对BP神经网络模型进行了系统性对比实验。
初始化方式对比表
| 初始化方式 | 神经元个数 | 网络层数 | 激活函数 | Accuracy | Loss |
|---|---|---|---|---|---|
| Xavier | 128 | 10 | ReLU | 0.9464 | 0.1807 |
| Kaiming | 128 | 10 | ReLU | 0.9444 | 0.1896 |
| Normal | 128 | 10 | ReLU | 0.7369 | 0.7285 |
| Uniform | 128 | 10 | ReLU | 0.9358 | 0.2252 |
最优选择:Xavier 初始化
表明对于BP神经网络而言,权重初始化方式对训练过程收敛速度和最终性能具有显著影响。Xavier初始化能够保持每层输出的方差一致,避免梯度消失或爆炸,从而提升训练稳定性。Normal初始化可能导致初始权重偏离过大,造成梯度传播困难。
神经元个数对比表
| 初始化方式 | 神经元个数 | 网络层数 | 激活函数 | Accuracy | Loss |
|---|---|---|---|---|---|
| Xavier | 64 | 10 | ReLU | 0.9389 | 0.2074 |
| Xavier | 128 | 10 | ReLU | 0.9464 | 0.1807 |
| Xavier | 256 | 10 | ReLU | 0.9497 | 0.1939 |
| Xavier | 512 | 10 | ReLU | 0.9421 | 0.2356 |
最佳神经元数量:256
实验发现,当神经元个数为 256 时,模型准确率达到最高(94.97%)。继续增大至512时,反而略有下降,说明神经元过多可能导致参数冗余,从而出现过拟合或训练不稳定。
网络层数对比表
| 初始化方式 | 神经元个数 | 网络层数 | 激活函数 | Accuracy | Loss |
|---|---|---|---|---|---|
| Xavier | 128 | 3 | ReLU | 0.9575 | 0.1391 |
| Xavier | 128 | 5 | ReLU | 0.9528 | 0.1506 |
| Xavier | 128 | 10 | ReLU | 0.9464 | 0.1807 |
| Xavier | 128 | 20 | ReLU | 0.9013 | 0.3571 |
最佳网络层数:3层
实验比较了 3、5、10、20 层的BP神经网络,发现3层网络的性能反而最好,准确率为 95.75%,而层数越多,效果反而逐渐下降,尤其在20层时准确率骤降至 90.13%,且Loss显著增大。
这说明对于结构简单的MNIST图像识别任务而言,过深的网络不仅不能提升表现,反而可能因为梯度消失或过拟合而降低性能。合理控制网络深度有助于模型的高效训练。
激活函数对比表
| 初始化方式 | 神经元个数 | 网络层数 | 激活函数 | Accuracy | Loss |
|---|---|---|---|---|---|
| Xavier | 128 | 10 | ReLU | 0.9464 | 0.1807 |
| Xavier | 128 | 10 | LeakyReLU | 0.9472 | 0.1801 |
| Xavier | 128 | 10 | Sigmoid | 0.3830 | 1.4522 |
| Xavier | 128 | 10 | Tanh | 0.9423 | 0.1984 |
最佳激活函数:LeakyReLU
在激活函数对比中,LeakyReLU略优于ReLU,表现为更低的Loss与更高的Accuracy。Tanh次之,而Sigmoid表现最差,准确率仅为38.30%,几乎无法完成任务。
CIFAR-10
初始化方式对比表
| 初始化方式 | 神经元个数 | 网络层数 | 激活函数 | Accuracy | Loss |
|---|---|---|---|---|---|
| Xavier | 128 | 10 | ReLU | 0.4099 | 1.6549 |
| Kaiming | 128 | 10 | ReLU | 0.3876 | 1.7094 |
| Normal | 128 | 10 | ReLU | 0.1703 | 2.0517 |
| Uniform | 128 | 10 | ReLU | 0.3209 | 1.7992 |
最优选择:Xavier 初始化
Xavier 初始化适用于对称激活函数(如 ReLU、Tanh),其在浅层到中等深度的网络结构中表现稳定。相比之下,Normal 初始化不具备前向信号的控制能力,容易导致梯度消失或爆炸,效果最差。
神经元个数对比表
| 初始化方式 | 神经元个数 | 网络层数 | 激活函数 | Accuracy | Loss |
|---|---|---|---|---|---|
| Xavier | 64 | 10 | ReLU | 0.4008 | 1.6731 |
| Xavier | 128 | 10 | ReLU | 0.4099 | 1.6549 |
| Xavier | 256 | 10 | ReLU | 0.4086 | 1.656 |
| Xavier | 512 | 10 | ReLU | 0.3893 | 1.7147 |
最佳神经元数量:128
进一步增加神经元并未带来显著提升,反而可能引起过拟合。
网络层数对比表
| 初始化方式 | 神经元个数 | 网络层数 | 激活函数 | Accuracy | Loss |
|---|---|---|---|---|---|
| Xavier | 128 | 3 | ReLU | 0.4389 | 1.5870 |
| Xavier | 128 | 5 | ReLU | 0.4357 | 1.5930 |
| Xavier | 128 | 10 | ReLU | 0.4099 | 1.6549 |
| Xavier | 128 | 20 | ReLU | 0.2254 | 1.9535 |
最佳网络层数:3层
深层全连接网络在缺乏卷积提取能力的前提下,面对复杂图像如 CIFAR-10 会迅速增加训练难度,出现训练不稳定、梯度消失等问题。而浅层结构能更快地捕捉全局特征,反而带来更优表现。
激活函数对比表
| 初始化方式 | 神经元个数 | 网络层数 | 激活函数 | Accuracy | Loss |
|---|---|---|---|---|---|
| Xavier | 128 | 10 | ReLU | 0.4099 | 1.6549 |
| Xavier | 128 | 10 | LeakyReLU | 0.4130 | 1.6456 |
| Xavier | 128 | 10 | Sigmoid | 0.1588 | 2.0878 |
| Xavier | 128 | 10 | Tanh | 0.3757 | 1.7548 |
最佳激活函数:LeakyReLU
LeakyReLU 在负区间仍保留微弱梯度,避免了神经元“失活”;但实际使用时,依然使用了ReLU测试数据。
CNN更换不同模块参数以探明作用:
初始化方式:Xavier / Kaiming / Normal / Uniform
卷积核个数:8、16、32、64
卷积层数:1、2、3、4
激活函数:ReLU / LeakyReLU / Sigmoid / Tanh
MNIST
初始化方式对比表
| 初始化方式 | 卷积核个数 | 卷积层数 | 激活函数 | Accuracy | Loss |
|---|---|---|---|---|---|
| Xavier | 16 | 3 | ReLU | 0.9799 | 0.0637 |
| Kaiming | 16 | 3 | ReLU | 0.9776 | 0.0742 |
| Normal | 16 | 3 | ReLU | 0.9658 | 0.1085 |
| Uniform | 16 | 3 | ReLU | 0.9780 | 0.0713 |
Xavier > Uniform > Kaiming > Normal
最佳初始化方式:Xavier
从准确率与损失函数表现来看,Xavier 初始化以 0.9799 的 Accuracy 和 0.0637 的 Loss 表现最佳,说明其在权重初始化时有更好的稳定性与收敛效果。
卷积核个数对比表
| 初始化方式 | 卷积核个数 | 卷积层数 | 激活函数 | Accuracy | Loss |
|---|---|---|---|---|---|
| Xavier | 8 | 3 | ReLU | 0.9799 | 0.0637 |
| Xavier | 16 | 3 | ReLU | 0.9728 | 0.0871 |
| Xavier | 32 | 3 | ReLU | 0.9803 | 0.0621 |
| Xavier | 64 | 3 | ReLU | 0.9842 | 0.0495 |
64 > 32 > 8 ≈ 16
最佳卷积核个数:64
卷积核个数从 8 到 64 呈现出较强的正向趋势,64 个卷积核时准确率最高,达到了 0.9842,且 Loss 最低,仅为 0.0495,说明在该任务中更丰富的卷积特征表达有助于提升分类性能。
卷积层数对比表
| 初始化方式 | 卷积核个数 | 卷积层数 | 激活函数 | Accuracy | Loss |
|---|---|---|---|---|---|
| Xavier | 16 | 1 | ReLU | 0.9729 | 0.0905 |
| Xavier | 16 | 2 | ReLU | 0.9768 | 0.754 |
| Xavier | 16 | 3 | ReLU | 0.9799 | 0.0637 |
| Xavier | 16 | 4 | ReLU | 0.9752 | 0.0810 |
3 层 > 2 层 > 4 层 > 1 层
最佳卷积层数:3 层
卷积层数增加到 3 层时模型性能最优,再往上反而性能下降。这表明在 MNIST 这种简单数据集上,过深的网络并不一定带来提升,反而可能导致特征过拟合或训练困难。
激活函数对比表
| 初始化方式 | 卷积核个数 | 卷积层数 | 激活函数 | Accuracy | Loss |
|---|---|---|---|---|---|
| Xavier | 16 | 3 | ReLU | 0.9799 | 0.0637 |
| Xavier | 16 | 3 | LeakyReLU | 0.9820 | 0.0580 |
| Xavier | 16 | 3 | Sigmoid | 0.9287 | 0.2467 |
| Xavier | 16 | 3 | Tanh | 0.9797 | 0.0649 |
LeakyReLU > ReLU ≈ Tanh > Sigmoid
最佳激活函数:LeakyReLU
在所有激活函数中,LeakyReLU 以 0.9820 的 Accuracy 和 0.0580 的 Loss 表现最优,略优于 ReLU,说明其在处理 ReLU 的“神经元死亡问题”方面更具优势。Sigmoid 明显不适合 CNN,收敛慢且梯度消失,效果最差。
CIFAR-10
初始化方式对比表
| 初始化方式 | 卷积核个数 | 卷积层数 | 激活函数 | Accuracy | Loss |
|---|---|---|---|---|---|
| Xavier | 16 | 3 | ReLU | 0.5685 | 1.2097 |
| Kaiming | 16 | 3 | ReLU | 0.5762 | 1.2068 |
| Normal | 16 | 3 | ReLU | 0.4612 | 1.4741 |
| Uniform | 16 | 3 | ReLU | 0.5463 | 1.2650 |
Kaiming>Xavier > Uniform > Normal
推荐初始化方式:Kaiming
卷积核个数对比表
| 初始化方式 | 卷积核个数 | 卷积层数 | 激活函数 | Accuracy | Loss |
|---|---|---|---|---|---|
| Xavier | 8 | 3 | ReLU | 0.5083 | 1.3704 |
| Xavier | 16 | 3 | ReLU | 0.5685 | 1.2097 |
| Xavier | 32 | 3 | ReLU | 0.6110 | 1.0978 |
| Xavier | 64 | 3 | ReLU | 0.6407 | 1.0130 |
64>32>16>8
最佳卷积核个数:64
卷积层数对比表
| 初始化方式 | 卷积核个数 | 卷积层数 | 激活函数 | Accuracy | Loss |
|---|---|---|---|---|---|
| Xavier | 16 | 1 | ReLU | 0.5556 | 1.2541 |
| Xavier | 16 | 2 | ReLU | 0.5630 | 1.2301 |
| Xavier | 16 | 3 | ReLU | 0.5685 | 1.2097 |
| Xavier | 16 | 4 | ReLU | 0.5400 | 1.241 |
3 层 > 2 层 > 1层 > 4 层
最佳卷积层数:3 层
依然是在底层到高层数表现为先增长,后减少,存在最优层数,避免过拟合的同时,又存在较好结果。
激活函数对比表
| 初始化方式 | 卷积核个数 | 卷积层数 | 激活函数 | Accuracy | Loss |
|---|---|---|---|---|---|
| Xavier | 16 | 3 | ReLU | 0.5685 | 1.2097 |
| Xavier | 16 | 3 | LeakyReLU | 0.5844 | 1.1684 |
| Xavier | 16 | 3 | Sigmoid | 0.3149 | 1.1278 |
| Xavier | 16 | 3 | Tanh | 0.6046 | 1.8902 |
Tanh>LeakyReLU > ReLU> Sigmoid
最佳激活函数:Tanh
Tanh中心对称的性质可能使得数据分布更加居中,有助于缓解梯度消失问题,从而在这个更大数据集,可能相对优势较大。
5.3 结果分析
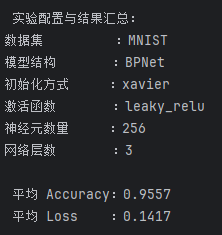
在前面的参数对比实验中,分别找出了初始化方式、激活函数、神经元个数和网络层数的“单项最优配置”,期望它们的组合能够带来“最优整体性能”。然而,组合结果却略低于部分单项测试下的最佳结果(如3层网络+ReLU时Accuracy达到了 0.9575,而最终组合结果为 0.9557),这说明最佳参数并非简单叠加得出。
原因分析:
参数间存在依赖与耦合:多个参数组合在一起时,其交互效应可能会导致性能打折扣。
浅层网络限制了其他参数的潜力:3层网络作为最优层数,这是在保持训练简单的基础上表现最好的结构,但它可能无法充分发挥复杂初始化(如Xavier)或激活函数(如LeakyReLU)带来的优势。
超参数之间存在“过拟合风险叠加”:虽然每个参数单独设置下不会引发过拟合,但组合在一起时,可能出现过度表达能力,导致在验证集上性能下降,尤其是Loss值升高。
因此最终仍然选择Xavier 128 3 ReLU作为MNIST数据集最优配置。
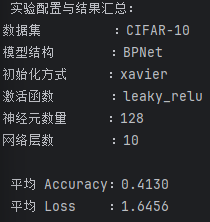
同样,在实验中,依然尝试将所有在单项实验中表现最优的超参数组合起来,形成“综合最优配置”,但实际上依然不如之前的测试结果,因此最终仍然选择Xavier 128 3 ReLU作为MNIST数据集最优配置。
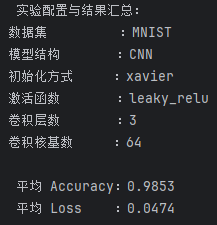
本次结果发现,综合采用各参数单项调优中表现最优的配置,即 Xavier 初始化、LeakyReLU 激活函数、3 层卷积结构以及64个基础卷积核,最终模型在 MNIST 数据集上取得了 0.9853 的平均准确率和 0.0474 的平均损失。但实际并非是组合起来的提升,因为我们看到这与所谓的”单项冠军“(Xavier 初始化、ReLU 激活函数、3 层卷积结构以及64个基础卷积核)只相差了激活函数,因此这项结论本质上还是单项的胜利,而非结合的结果。
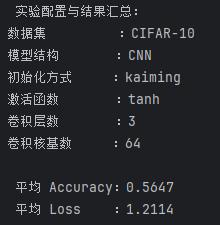
在本次CNN模型训练CIFAR-10数据集中,成功取得综合最优的体现,通过枚举的方法,最终采用 Kaiming 初始化、Tanh 激活函数、3 层卷积结构以及卷积核基数为 64 的 CNN 模型在 CIFAR-10 数据集上取得了最佳性能,平均准确率达到 0.5647,损失值为 1.2114,相较于其他配置均有明显优势。
后经查询分析,得到原因可能如下:这一组合能够充分利用 Kaiming 初始化在深度网络中对梯度稳定的优化效果,同时 Tanh 激活函数在 CIFAR-10 这类自然图像数据上展现出更强的非线性表达能力和稳定性,配合较深且足够宽的网络结构,有助于提取更丰富的图像特征,从而在分类任务中表现更优。
六、实验结论
在本次实验中,我们系统性地掌握了深度学习模型的编程实现过程,包括如何使用 PyTorch 框架加载标准图像数据集(MNIST 与 CIFAR-10)、构建可配置的神经网络模型(BP 与 CNN)、执行 K 折交叉验证训练模型,以及如何灵活调整网络结构参数以优化模型性能。
通过本次实验,也加深了对超参数在模型训练中的影响的理解,我们观察到模型表现受初始化方式、激活函数、网络层数和神经元/卷积核数量等多个因素的影响,并非所有参数的“最优”组合都能带来“最优”的整体结果,说明它们之间存在复杂的相互作用和依赖关系。尤其是在浅层网络中,部分复杂配置的优势无法完全体现,甚至可能因参数冗余导致性能下降。
在未来的研究中,测试更多的可能数据,尝试更多的横向对比,同时进行更多的组合,但由于本次实验数据量和训练时间的限制(如果全部测出,会跑4^5=1024次代码),我们未能进行更大规模的实验;此外,还可以尝试引入参数敏感性分析或可视化方法,更量化地评估各超参数对模型性能的贡献,从而实现更高效、自动化的模型调优。
本次实验不仅提升了我们对深度学习模型的工程实践能力,也帮助我们理解了人工智能模型在海量数据中的构建与优化思路。这为以后进行海洋数据分析和处理,提供了很大的帮助!
七、实验数据与代码
实验源代码
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchvision import datasets, transforms
from torch.utils.data import DataLoader, Subset
from sklearn.model_selection import KFold
from sklearn.metrics import accuracy_score, log_loss, roc_curve, auc
from sklearn.preprocessing import label_binarize
import matplotlib.pyplot as plt
import numpy as np
# ========== 设置随机种子 ==========
seed = 42
torch.manual_seed(seed)
np.random.seed(seed)
# ========== 参数配置 ==========
k_folds = 5
batch_size = 64
use_mnist = True
model_type = 'cnn'
epochs = 1
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# ========== 模型定义 ==========
class DeepBPNet(nn.Module):def __init__(self, input_size=784, hidden_size=128, num_classes=10, num_layers=10, activation='relu', init_method='xavier'):super(DeepBPNet, self).__init__()assert num_layers >= 2, "网络层数必须 >= 2"self.activation_fn = self._get_activation_fn(activation)self.input_layer = nn.Linear(input_size, hidden_size)self.hidden_layers = nn.ModuleList([nn.Linear(hidden_size, hidden_size) for _ in range(num_layers - 2)])self.output_layer = nn.Linear(hidden_size, num_classes)self.init_weights(method=init_method)
def forward(self, x):x = x.view(x.size(0), -1)x = self.activation_fn(self.input_layer(x))for layer in self.hidden_layers:x = self.activation_fn(layer(x))x = self.output_layer(x)return x
def _get_activation_fn(self, name):return {'relu': nn.ReLU(),'tanh': nn.Tanh(),'sigmoid': nn.Sigmoid(),'leaky_relu': nn.LeakyReLU(0.1)}.get(name.lower(), nn.ReLU())
def init_weights(self, method='xavier'):for m in self.modules():if isinstance(m, nn.Linear):if method == 'xavier':nn.init.xavier_uniform_(m.weight)elif method == 'kaiming':nn.init.kaiming_normal_(m.weight, nonlinearity='relu')elif method == 'normal':nn.init.normal_(m.weight, mean=0.0, std=0.02)elif method == 'uniform':nn.init.uniform_(m.weight, a=-0.1, b=0.1)if m.bias is not None:nn.init.zeros_(m.bias)
class CustomCNN(nn.Module):def __init__(self, in_channels=1, input_size=(28,28), num_classes=10, conv_layers=3, base_channels=16, activation='relu', init_method='xavier'):super(CustomCNN, self).__init__()assert conv_layers >= 1, "至少要有一个卷积层"self.activation_fn = self._get_activation_fn(activation)self.conv_blocks = nn.ModuleList()channels = in_channels
for i in range(conv_layers):out_channels = base_channels * (2 ** i)self.conv_blocks.append(nn.Sequential(nn.Conv2d(channels, out_channels, kernel_size=3, padding=1),self.activation_fn,nn.MaxPool2d(2, 2)))channels = out_channels
dummy_input = torch.zeros(1, in_channels, *input_size)with torch.no_grad():for layer in self.conv_blocks:dummy_input = layer(dummy_input)flatten_dim = dummy_input.view(1, -1).shape[1]
self.fc1 = nn.Linear(flatten_dim, 128)self.fc2 = nn.Linear(128, num_classes)self.init_weights(init_method)
def forward(self, x):for layer in self.conv_blocks:x = layer(x)x = x.view(x.size(0), -1)x = self.activation_fn(self.fc1(x))x = self.fc2(x)return x
def _get_activation_fn(self, name):return {'relu': nn.ReLU(),'tanh': nn.Tanh(),'sigmoid': nn.Sigmoid(),'leaky_relu': nn.LeakyReLU(0.1)}.get(name.lower(), nn.ReLU())
def init_weights(self, method='xavier'):for m in self.modules():if isinstance(m, (nn.Conv2d, nn.Linear)):if method == 'xavier':nn.init.xavier_uniform_(m.weight)elif method == 'kaiming':nn.init.kaiming_normal_(m.weight, nonlinearity='relu')elif method == 'normal':nn.init.normal_(m.weight, mean=0.0, std=0.02)elif method == 'uniform':nn.init.uniform_(m.weight, a=-0.1, b=0.1)if m.bias is not None:nn.init.zeros_(m.bias)
# ========== 数据读取与预处理模块 ==========
def load_dataset(use_mnist=True):if use_mnist:transform = transforms.Compose([transforms.ToTensor(),transforms.Normalize((0.1307,), (0.3081,))])dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)else:transform = transforms.Compose([transforms.ToTensor(),transforms.Normalize((0.5,), (0.5,))])dataset = datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)print(f"加载数据集完成:{len(dataset)}张图像,尺寸为 {dataset[0][0].shape}")return dataset
# ========== 数据与模型接口 ==========
def get_model(model_type='bp', input_shape=(1, 28, 28), num_classes=10, **kwargs):if model_type == 'bp':input_size = np.prod(input_shape)return DeepBPNet(input_size=input_size, num_classes=num_classes, **kwargs)elif model_type == 'cnn':return CustomCNN(in_channels=input_shape[0], input_size=input_shape[1:], num_classes=num_classes, **kwargs)else:raise ValueError("模型必须是'bp'或者'cnn'")
# ========== 模型评估模块 ==========
def evaluate_model_kfold(dataset, model_type='cnn', k_folds=5, batch_size=64, num_classes=10, device=None, epochs=1, **kwargs):if device is None:device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
indices = list(range(len(dataset)))kf = KFold(n_splits=k_folds, shuffle=True, random_state=42)
all_fold_metrics = []all_probs = []all_targets = []
for fold, (train_idx, val_idx) in enumerate(kf.split(indices)):print(f"\n 训练轮数 {fold + 1}/{k_folds}")
train_subset = Subset(dataset, train_idx)val_subset = Subset(dataset, val_idx)train_loader = DataLoader(train_subset, batch_size=batch_size, shuffle=True)val_loader = DataLoader(val_subset, batch_size=batch_size, shuffle=False)
sample_input, _ = next(iter(train_loader))model = get_model(model_type=model_type,input_shape=sample_input.shape[1:],num_classes=num_classes,**kwargs).to(device)
criterion = nn.CrossEntropyLoss()optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
# === 训练阶段 ===model.train()for epoch in range(epochs):for inputs, labels in train_loader:inputs, labels = inputs.to(device), labels.to(device)optimizer.zero_grad()outputs = model(inputs)loss = criterion(outputs, labels)loss.backward()optimizer.step()
# === 验证阶段 ===model.eval()y_true, y_pred, y_prob = [], [], []
with torch.no_grad():for inputs, labels in val_loader:inputs, labels = inputs.to(device), labels.to(device)outputs = model(inputs)probs = F.softmax(outputs, dim=1)preds = torch.argmax(probs, dim=1)
y_true.extend(labels.cpu().numpy())y_pred.extend(preds.cpu().numpy())y_prob.extend(probs.cpu().numpy())
acc = accuracy_score(y_true, y_pred)loss = log_loss(y_true, y_prob, labels=list(range(num_classes)))
all_fold_metrics.append({'fold': fold + 1, 'accuracy': acc, 'loss': loss})all_probs.extend(y_prob)all_targets.extend(y_true)
print(f" Fold {fold + 1} Accuracy: {acc:.4f}, Loss: {loss:.4f}")
return all_fold_metrics, np.array(all_probs), np.array(all_targets)
# ========== 模型评估可视化模块 ==========
def plot_multiclass_roc(probs, targets, num_classes, save_path=None):targets_onehot = label_binarize(targets, classes=list(range(num_classes)))
fpr = dict()tpr = dict()roc_auc = dict()
for i in range(num_classes):fpr[i], tpr[i], _ = roc_curve(targets_onehot[:, i], probs[:, i])roc_auc[i] = auc(fpr[i], tpr[i])
plt.figure(figsize=(10, 8))for i in range(num_classes):plt.plot(fpr[i], tpr[i], label=f"Class {i} (AUC = {roc_auc[i]:.2f})")
plt.plot([0, 1], [0, 1], 'k--', label='Random')plt.xlim([0.0, 1.0])plt.ylim([0.95, 1.05])plt.xlabel('假警报率')plt.ylabel('识别率')plt.title('多分类模型的ROC曲线')plt.rcParams['font.sans-serif'] = ['SimHei']plt.legend(loc='lower right')
if save_path:plt.savefig(save_path)print(f" ROC曲线已保存到 {save_path}")else:plt.show()
# ========== 主程序入口 ==========
if __name__ == '__main__':# === 数据集选择 ===print("请选择数据集:")print("1 - MNIST")print("2 - CIFAR-10")dataset_choice = input("请输入选项(1 或 2):").strip()if dataset_choice == '1':use_mnist = Trueelif dataset_choice == '2':use_mnist = Falseelse:print("无效输入,默认使用 MNIST")use_mnist = True
# === 模型结构选择 ===print("\n请选择模型结构:")print("1 - CNN(卷积神经网络)")print("2 - BPNet(多层感知机)")model_choice = input("请输入选项(1 或 2):").strip()if model_choice == '1':model_type = 'cnn'elif model_choice == '2':model_type = 'bp'else:print("无效输入,默认使用 CNN")model_type = 'cnn'
# === 初始化方式选择 ===print("\n请选择初始化方式:")print("1 - Xavier(推荐)")print("2 - Kaiming")print("3 - Normal")print("4 - Uniform")init_choice = input("请输入选项(1~4):").strip()init_method = {'1': 'xavier','2': 'kaiming','3': 'normal','4': 'uniform'}.get(init_choice, 'xavier')if init_choice not in ['1', '2', '3', '4']:print("无效输入,默认使用 Xavier 初始化")
# === 激活函数选择 ===print("\n请选择激活函数:")print("1 - ReLU")print("2 - LeakyReLU")print("3 - Tanh")print("4 - Sigmoid")act_choice = input("请输入选项(1~4):").strip()activation = {'1': 'relu','2': 'leaky_relu','3': 'tanh','4': 'sigmoid'}.get(act_choice, 'relu')if act_choice not in ['1', '2', '3', '4']:print("无效输入,默认使用 ReLU 激活函数")
# === 网络结构参数(根据模型类型设置) ===extra_args = {}if model_type == 'bp':hidden_size = input("\n请输入每层的神经元数量(默认128):").strip()num_layers = input("请输入网络层数(最少2层,默认10):").strip()extra_args['hidden_size'] = int(hidden_size) if hidden_size.isdigit() else 128extra_args['num_layers'] = int(num_layers) if num_layers.isdigit() else 10# 将激活函数传递给BP网络extra_args['activation'] = activationelif model_type == 'cnn':conv_layers = input("\n请输入卷积层数(默认3):").strip()base_channels = input("请输入基础卷积核个数(默认16):").strip()extra_args['conv_layers'] = int(conv_layers) if conv_layers.isdigit() else 3extra_args['base_channels'] = int(base_channels) if base_channels.isdigit() else 16extra_args['activation'] = activation
extra_args['init_method'] = init_method
# === 加载数据 & 开始训练 ===dataset = load_dataset(use_mnist=use_mnist)metrics, probs, targets = evaluate_model_kfold(dataset=dataset,model_type=model_type,k_folds=k_folds,batch_size=batch_size,num_classes=10,device=device,epochs=epochs,**extra_args # 💡传入模型构建参数)
print("\n 每折评估结果:")for result in metrics:print(f"Fold {result['fold']} - Accuracy: {result['accuracy']:.4f}, Loss: {result['loss']:.4f}")
# === 绘制 ROC 曲线图 ===plot_multiclass_roc(probs=probs, targets=targets, num_classes=10)
# === 输出整体实验配置信息和平均结果 ===avg_acc = np.mean([fold['accuracy'] for fold in metrics])avg_loss = np.mean([fold['loss'] for fold in metrics])
print("\n 实验配置与结果汇总:")print(f"数据集 :{'MNIST' if use_mnist else 'CIFAR-10'}")print(f"模型结构 :{'BPNet' if model_type == 'bp' else 'CNN'}")print(f"初始化方式 :{init_method}")if model_type == 'cnn':print(f"激活函数 :{activation}")print(f"卷积层数 :{extra_args['conv_layers']}")print(f"卷积核基数 :{extra_args['base_channels']}")else:print(f"激活函数 :{activation}")print(f"神经元数量 :{extra_args['hidden_size']}")print(f"网络层数 :{extra_args['num_layers']}")
print(f"\n 平均 Accuracy:{avg_acc:.4f}")print(f" 平均 Loss :{avg_loss:.4f}")
)



如何使用MySQL的慢查询工具?)
)













缓存区)