光束质量分析仪是用于精确评估激光光束特性的核心设备，通过测量光束的强度分布、相位分布、发散角等参数，为激光系统的优化、加工工艺控制及科研实验提供关键数据支持。

以下是光束质量分析仪的详细解析：

一、核心功能 - 光束强度分布分析

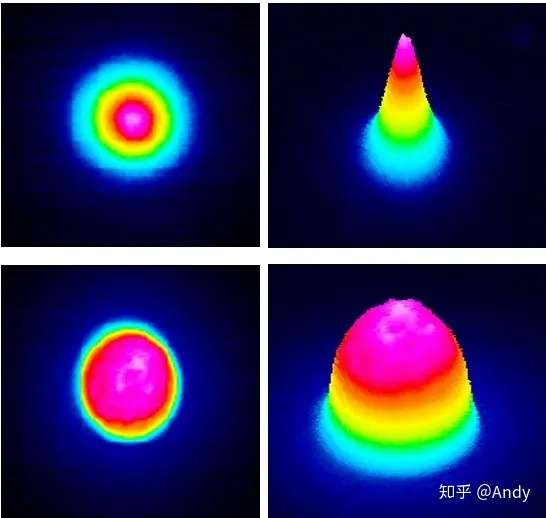
测量内容：获取光束在横截面上的能量分布（如高斯分布、平顶分布、多模分布等）。
应用场景：判断激光模式（TEM₀₀基模或多模）、优化谐振腔设计、调整光束整形器件（如扩束镜、透镜组）。

光束强度分布是描述激光或其他光束在横截面上能量（或光强）随空间位置变化的函数，是光束质量评估、光学系统设计和应用优化的核心参数。以下从定义、理论模型、测量方法、影响因素及应用场景五个方面展开解析：

1.1、定义与物理意义

定义：
- 光束强度分布（Beam Intensity Profile）指光束横截面上单位面积的光功率（或光强）随坐标（x,y）的变化关系，通常表示为 I(x,y)。
- 对于旋转对称光束（如TEM₀₀模），可简化为径向分布 I(r)，其中 r=x2+y2。
物理意义：
- 反映光束的能量集中度：中心强度高、边缘衰减的光束（如高斯分布）能量集中；均匀分布的光束（如平顶光束）能量分散。
- 决定光束与物质相互作用的特性：如切割深度、焊接熔宽、粒子囚禁效率等。

1.2、理论模型：常见光束强度分布类型

1. 高斯分布（TEM₀₀模）

数学表达式：

I(r)=I0exp(−w022r2)

其中：

I0 为束腰中心光强，
w0 为束腰半径，
r 为径向坐标。
特点：
- 强度随半径平方指数衰减，边缘光强趋近于零。
- 能量集中在中心区域（约95%能量在 2w0 直径内）。
- 适用于单模激光（如He-Ne激光、光纤激光器基模输出）。

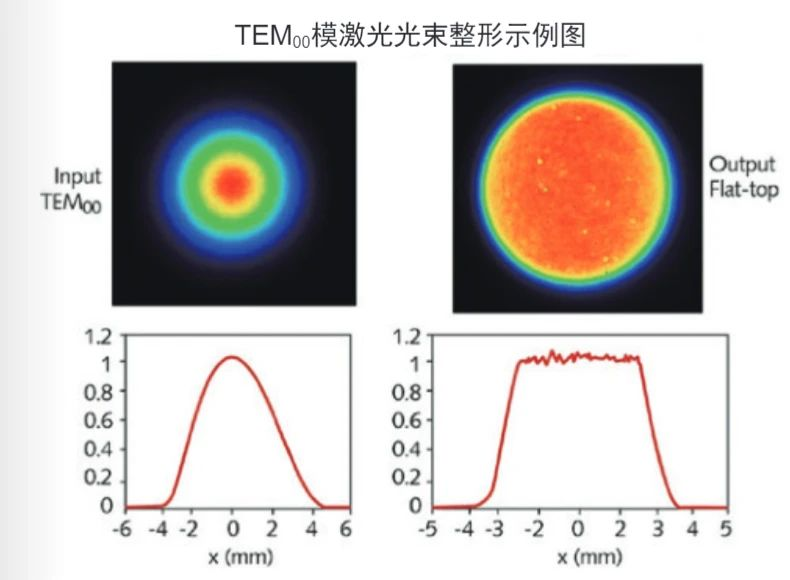
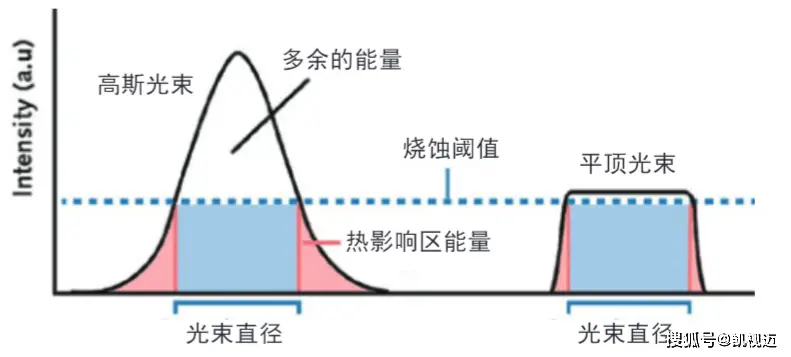
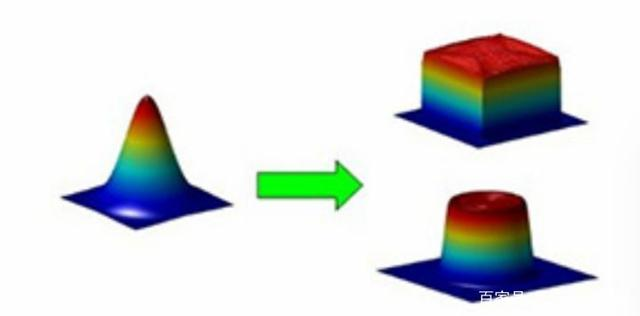
2. 平顶分布（Top-Hat Profile）

数学表达式：

I(r)={I00if r≤Rif r>R

其中 R 为光束半径。

特点：
- 强度在中心区域均匀，边缘锐截止。
- 能量利用率高（无边缘衰减），但实际中难以实现完全平顶。
- 适用于激光加工（如均匀切割、焊接）和光学镊子。

3. 环形分布（Doughnut Profile）

数学表达式：

I(r)=I0⋅w02r2exp(−w02r2)

（拉盖尔-高斯模的特例）

特点：
- 中心光强为零，强度在环形区域最大。
- 适用于光学涡旋（如轨道角动量光束）和粒子旋转操控。

4. 多模分布（Higher-Order Modes）

数学表达式：
- 由多个高斯模叠加而成，如厄米-高斯模（矩形对称）或拉盖尔-高斯模（圆柱对称）。
- 例如，TEM₁₀模：

I(x)∝x2exp(−w022x2)

特点：
- 强度分布出现多峰或复杂结构（如十字形、环形加中心斑）。
- 常见于多模激光器或腔模失配的光束。

1.3、测量方法

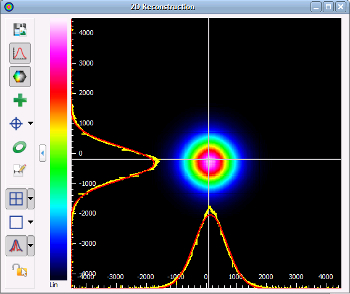
1. CCD/CMOS成像法

原理：
- 用相机直接捕获光束横截面图像，通过软件分析像素灰度值（与光强成正比）。
步骤：
1. 扩展光束至相机感光面（避免饱和）。
2. 采集多帧图像，取平均值减少噪声。
3. 拟合强度分布曲线（如高斯拟合）。X和Y轴两个方向。
优点：
- 非接触、实时、可视化。
- 适用于动态光束监测（如光束漂移）。
缺点：
- 需校准像素尺寸与实际尺寸的对应关系。
- 高功率光束需衰减片防止相机损坏。

2. 刀口法（Knife-Edge Method）

原理：
- 用锐利刀片横向切割光束，测量光功率随刀片位置的变化，反推强度分布。
步骤：
1. 固定激光器，移动刀片逐步遮挡光束。
2. 记录光功率 P 随刀片位置 x 的变化曲线。
3. 对 dP/dx 求导得到强度分布 I(x)。
优点：
- 简单、成本低，适用于高功率光束。
- 可直接测量一维强度分布。
缺点：
- 需手动操作，精度受刀片锐度影响。
- 无法直接获取二维分布（需旋转刀片多次测量）。

3. 扫描探针法（Scanning Probe Method）

原理：
- 用光电探针（如光电二极管）在光束横截面上扫描，记录光强随位置的变化。
步骤：
1. 固定探针，移动激光器或反射镜使光束扫描过探针。
2. 记录探针输出信号随时间的变化。
3. 转换为空间分布，拟合强度参数。
优点：
- 适用于高功率激光（探针可远离光束中心）。
- 可测量超快光束（需高速探针）。
缺点：
- 机械扫描速度慢，可能引入振动误差。
- 需精确控制扫描路径。

1.4、影响因素

激光模式：
- 单模激光（TEM₀₀）为高斯分布，多模激光为复杂分布（如多峰、环形）。
- 模式纯度越高，强度分布越接近理论模型。
光学元件损伤：
- 高功率光束中，光学元件（如透镜、镜片）的损伤可能导致强度分布畸变（如中心凹陷）。
像差与波前畸变：
- 透镜像差（如球差、色差）会破坏高斯分布的对称性。
- 自适应光学可校正波前畸变，优化强度分布。
非线性效应：
- 高功率下，克尔效应或自聚焦效应可能改变强度分布（如光束自收缩或分裂）。

1.5、应用场景

激光加工：
- 切割/焊接：高斯分布光束的能量集中，适合精细加工；平顶分布光束适合大面积均匀处理。
- 钻孔：环形分布光束可实现高深径比微孔加工。
光学测量：
- 干涉仪：强度分布均匀性影响干涉条纹对比度。
- 全息术：平顶分布光束可提高全息图信噪比。
生物医学：
- 光学镊子：高斯分布光束用于囚禁微粒；环形分布光束用于旋转操控。
- 光热治疗：强度分布决定组织加热区域（如肿瘤靶向治疗）。
量子光学：
- 冷原子实验：高斯分布光束的强度梯度用于磁光阱中原子冷却与囚禁。
- 光子纠缠：强度分布影响双光子干涉可见度。

1.6、实际案例：高斯光束强度分布的测量与验证

案例1：He-Ne激光器（632.8 nm）

测量步骤：
1. 用扩束镜将光束扩展至CCD感光面（直径约5 mm）。
2. 采集图像并拟合高斯曲线：

I(r)=I0exp(−w022r2)

测得束腰半径 w0=150μm，中心光强 I0=10mW/cm2。

验证：
- 计算理论发散角：

θ=πw0λ=π×150×10−6632.8×10−9≈1.35mrad

与实际测量发散角（1.4 mrad）吻合，验证高斯分布假设。

案例2：光纤激光器平顶光束生成

方法：
- 在光纤激光器输出端插入衍射光学元件（DOE），将高斯分布转换为平顶分布。
效果：
- 平顶光束直径 2R=1mm，边缘锐度 < 5%。
- 应用于太阳能电池焊接，熔宽均匀性提升30%。

二、TEM₀₀基模或多模

TEM₀₀基模和多模是激光光束的两种基本模式类型，它们在光束特性、应用场景及测量方法上存在显著差异。以下是详细解析：

2.1、TEM₀₀基模：理想高斯光束

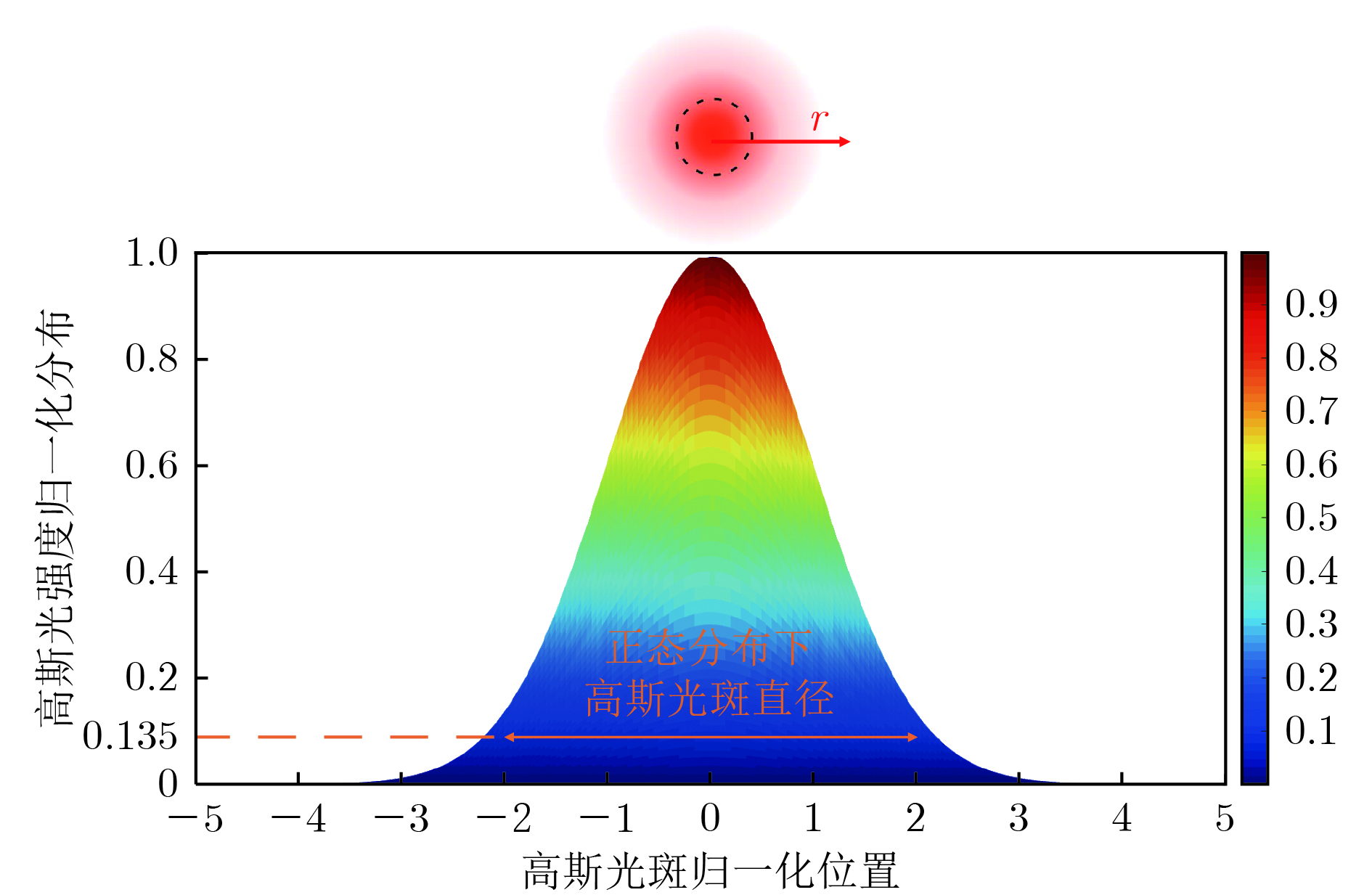
1. 定义与特性

模式定义：TEM₀₀（Transverse Electromagnetic Mode）是激光谐振腔中最低阶的横模，其电场和磁场在横截面上呈高斯分布，无任何节点或暗环。
核心特性：
- 光束强度分布：中心强度最高，向边缘呈指数衰减，形成典型的高斯轮廓。
- 光束宽度：在束腰处（最小截面）的光束直径最小，且沿传播方向按双曲线规律发散。
- M²因子：理论上M²=1（实际因光学元件缺陷可能略大于1），表示光束质量接近理想。
- 相位分布：波前为平面波（在束腰处）或球面波（远离束腰），相位畸变极小。

2. 优势与应用

优势：
- 高聚焦性：可聚焦到极小光斑（如衍射极限光斑），适用于高精度加工。
- 低发散角：长距离传输时能量集中，减少损耗。
- 稳定性高：模式纯净，抗干扰能力强。
典型应用：
- 激光切割/焊接：高能量密度实现精密加工（如薄板切割、微焊接）。
- 激光打标：生成清晰、高对比度的标记。
- 光学测量：作为标准光束校准光学系统。
- 科研领域：如冷原子实验、量子光学研究等。

3. 测量与评估

光束质量分析仪：
- 强度分布测量：通过CCD或CMOS相机捕获光束横截面图像，拟合高斯曲线计算束腰直径。
- M²因子测试：沿光束传播方向多点测量束腰直径与发散角，计算M²值（越接近1越好）。
- 波前传感器：检测相位分布，确认无显著畸变。

2.2、多模：复杂光束的混合态

1. 定义与特性

模式定义：多模指光束中同时存在多个横模（如TEM₀₁、TEM₁₀、TEM₁₁等）的叠加，形成复杂强度分布。

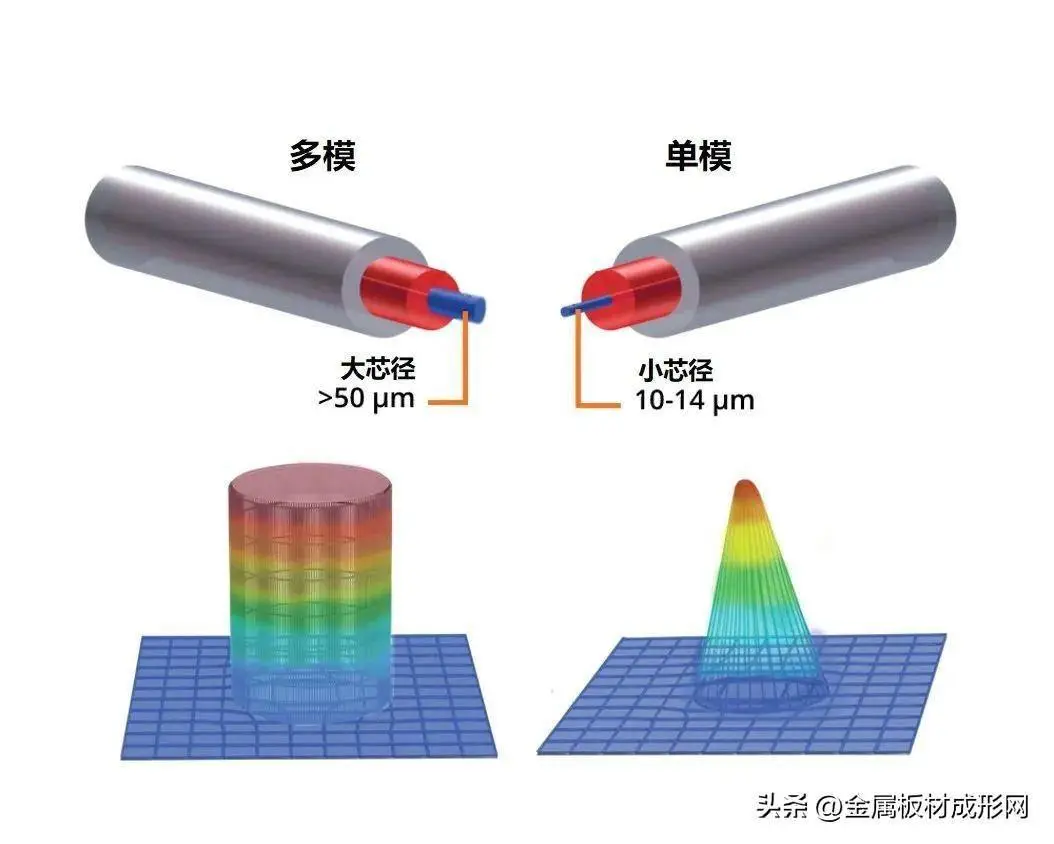
核心特性：
- 光束强度分布：中心可能存在多个峰值或暗环，轮廓不规则（如平顶分布、环形分布等）。
- 光束宽度：束腰直径通常大于同功率的TEM₀₀模，且发散角更大。
- M²因子：M²>1（数值越大表示光束质量越差，越远离理想的高斯光束TEM₀₁），因模式混合导致能量分散。
- 相位分布：波前存在显著畸变，可能包含像差或高阶相位项。

2. 优势与应用

优势：
- 高功率输出：多模激光器（如光纤激光器）可通过模式混合提升总功率。
- 均匀能量分布：平顶多模光束适用于大面积均匀加工（如表面处理、涂层固化）。
- 成本较低：多模激光器结构简单，易于大规模生产。
典型应用：
- 激光焊接（厚板）：多模光束的较大光斑和深熔池提高焊接效率。
- 激光熔覆：平顶分布实现均匀涂层沉积。
- 材料处理：如激光清洗、表面改性等。
- 医疗美容：如激光脱毛、皮肤再生等（需控制光斑均匀性）。

3. 测量与评估

光束质量分析仪：
- 强度分布测量：捕获光束横截面图像，分析模式成分（如通过傅里叶变换分解横模）。
- M²因子测试：沿传播方向多点测量，计算综合M²值（通常>5）。
- 波前传感器：检测复杂相位畸变，评估模式混合程度。
挑战：
- 模式分解复杂：需高级算法（如模式匹配法）区分多个横模。
- 动态变化监测：多模光束可能随时间或环境变化（如温度漂移导致模式竞争）。

2.3、TEM₀₀基模与多模的对比总结

特性	TEM₀₀基模	多模
强度分布	高斯分布（单峰）	复杂分布（多峰、环形、平顶等）
光束宽度	最小（衍射极限）	较大（模式混合导致）
发散角	小（准直性好）	大（能量分散）
M²因子	≈1（理想）	>1（通常>5）
聚焦能力	极强（可聚焦到微米级）中心点的能量极高	较弱（光斑较大）
功率容量	较低（高功率易损坏光学元件）	高（适合千瓦级激光）
应用场景	精密加工、科研、测量	厚板焊接、大面积处理、工业制造
测量难度	较低（标准高斯拟合）	较高（需模式分解算法）

2.4、选型建议：根据需求选择模式

追求高精度/小光斑：
- 优先选择TEM₀₀基模激光器（如固体激光器、半导体激光器）。
- 配合光束质量分析仪严格监控M²因子，确保模式纯净。
需要高功率/大面积加工：
- 选择多模激光器（如光纤激光器、CO₂激光器）。
- 通过光束整形器（如扩束镜、平顶转换器）优化能量分布。
平衡成本与性能：
- 中低功率应用可考虑部分相干光源（如多模半导体激光器），兼顾成本与效率。

2.5、未来趋势：模式控制技术

自适应光学：
- 通过变形镜实时补偿波前畸变，将多模光束转换为近TEM₀₀模。
模式选择腔：
- 设计特殊谐振腔结构（如非稳腔、偏振选择腔），强制输出单一横模。
相干合成技术：
- 将多个多模激光束通过相位锁定合成高功率TEM₀₀模光束。

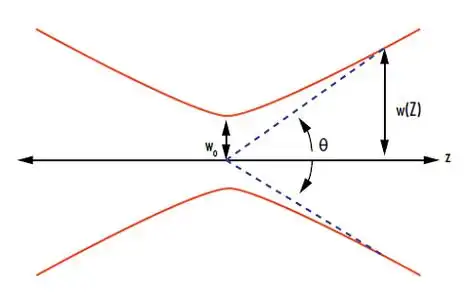
三、核心功能 - 光束宽度（束腰直径）

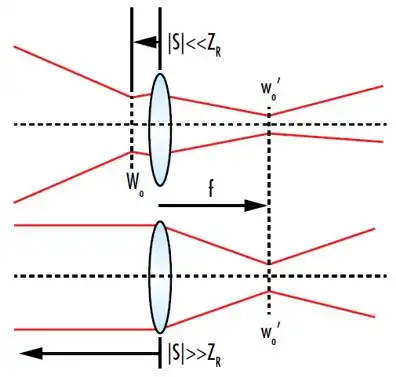
光束宽度（束腰直径）是描述激光光束在横截面上最小尺寸的核心参数，尤其在TEM₀₀基模中，它直接决定了光束的聚焦能力、能量密度和传播特性。

以下是关于光束宽度（束腰直径）的详细解析：

3.1、定义与物理意义

定义：
- 束腰直径（Beam Waist Diameter, 2w0）：指激光光束在传播方向上横截面最小处的直径，即光束最细的位置（焦点的位置）。
- 束腰半径（w0）：束腰直径的一半，是国际标准中更常用的参数。
物理意义：
- 束腰是光束的“聚焦点”，其尺寸决定了光束的能量集中度。
- 在束腰处，光束的发散角最小，波前为平面波（理想情况下），是光束质量评估的关键参考点。

3.2、TEM₀₀基模中的束腰直径

高斯光束特性：
- TEM₀₀模的光束强度呈高斯分布，束腰处的光强最大，向边缘按指数衰减。
- 束腰直径是光束的“最小可实现尺寸”，受衍射极限限制。
计算公式：
- 束腰半径 w0 与激光谐振腔参数的关系：

w0=πλL⋅g1+g2−2g1g2g2

其中：

- $\lambda$ 为激光波长，

- $L$ 为谐振腔长度，

- $g_1, g_2$ 为谐振腔的几何参数（$g_i = 1 - \frac{L}{R_i}$，$R_i$ 为腔镜曲率半径）。

简化公式（对称共焦腔）：

w0≈πλL

此时束腰位于谐振腔中心，尺寸最小。

3. 实际测量中的近似：

通过光束质量分析仪测量光束强度分布，拟合高斯曲线，直接读取束腰直径（2w0）。
常用方法：刀口法、CCD成像法、移动探针法等。

3.3、束腰直径的影响因素

激光波长（λ）：
- 波长越长，束腰直径越大（衍射效应增强），波长越小，粒子性越强，束腰直径越小。
- 例如：CO₂激光（10.6 μm）的束腰通常比Nd:YAG激光（1.06 μm）更粗。
谐振腔设计：
- 腔长（L）：腔长越长，束腰直径越大（光束有更多空间发散）。
- 腔镜曲率（R）：曲率半径越小，束腰越细（光束被更强聚焦）。
- 模式选择元件：如孔径光阑、偏振片可抑制高阶模，维持TEM₀₀模的细束腰。
光学元件损伤：
- 高功率激光中，光学元件（如透镜、镜片）的损伤阈值限制了束腰的最小尺寸。
- 束腰过细会导致局部功率密度过高，可能损坏元件。

3.4、束腰直径的测量方法

刀口法（Knife-Edge Method）：
- 原理：用锐利刀片横向切割光束，测量光强随刀片位置的变化，拟合高斯曲线确定束腰。
- 步骤：
  1. 固定激光器，移动刀片逐步遮挡光束。
  2. 记录光功率随刀片位置的变化曲线。
  3. 拟合曲线得到束腰半径 w0。
- 优点：简单、成本低。
- 缺点：需手动操作，精度受刀片锐度影响。
CCD成像法：
- 原理：用CCD或CMOS相机捕获光束横截面图像，通过软件分析强度分布。
- 步骤：
  1. 将激光聚焦到CCD感光面。
  2. 采集多帧图像，取平均值减少噪声。
  3. 拟合高斯曲线，计算束腰直径。
- 优点：非接触、自动化、可实时监测。
- 缺点：需校准相机像素尺寸与实际尺寸的对应关系。
移动探针法（Scanning Probe Method）：
- 原理：用光电探针（如光电二极管）在光束横截面上扫描，测量光强分布。
- 步骤：
  1. 固定探针，移动激光器或反射镜使光束扫描过探针。
  2. 记录探针输出信号随时间的变化。
  3. 转换为空间分布，拟合束腰参数。
- 优点：适用于高功率激光（探针可远离光束中心）。
- 缺点：机械扫描速度慢，可能引入振动误差。

3.5、束腰直径的应用场景

激光加工：
- 切割/焊接：细束腰（微米级）可实现高精度加工（如半导体晶圆切割）。
- 打标：束腰直径决定标记线条的粗细（如二维码的最小尺寸）。
光学测量：
- 干涉仪：束腰作为参考光束，其尺寸影响干涉条纹的对比度。
- 全息术：细束腰可提高全息图的分辨率。
科研领域：
- 冷原子实验：束腰直径决定原子囚禁区域的体积（如磁光阱的尺寸）。
- 量子光学：束腰与光子模式体积相关，影响光与物质相互作用效率。

3.6、束腰直径的优化策略！！！！！！！！！！

缩短谐振腔长：
- 减少腔长 L 可直接减小束腰直径（但需平衡腔稳定性）。
使用小曲率半径腔镜：
- 选择曲率半径 R 较小的腔镜，增强光束聚焦效果。
插入模式选择元件：
- 在腔内放置孔径光阑或偏振片，抑制高阶模，维持TEM₀₀模的细束腰。
自适应光学补偿：
- 用变形镜实时校正波前畸变，优化束腰尺寸和形状。

3.7、实际案例：束腰直径的计算与测量

案例1：He-Ne激光器（632.8 nm）

谐振腔长 L=30 cm，腔镜曲率 R1=R2=1 m。
计算 g1=g2=1−10.3=0.7。
代入公式：

w0=π632.8×10−9×0.3⋅0.7+0.7−2×0.70.7≈160μm

（注：此例中分母为零，需用更精确的谐振腔理论计算，实际束腰可能更小。）

案例2：光纤激光器（1064 nm）

通过CCD测量束腰直径为 50μm。
计算发散角：

θ=πw0λ=π×25×10−61064×10−9≈13.5mrad

（发散角与束腰直径成反比，细束腰导致大发散角。）

四、核心功能 - 发散角

发散角：计算光束远场发散角，评估光束的准直性。

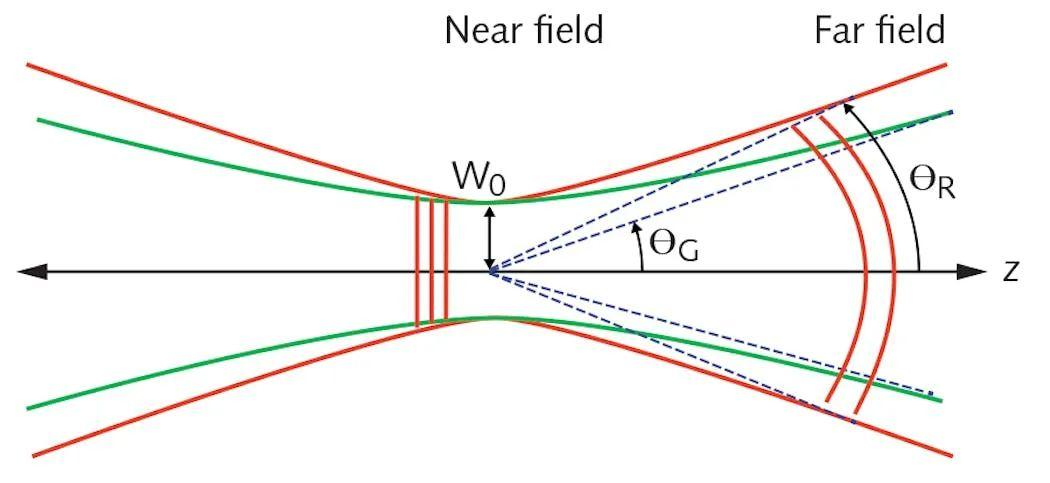
发散角（Divergence Angle）是描述光束在传播过程中空间扩展特性的关键参数，定义为光束远场（距离光源足够远）时，光强下降至中心最大值一定比例（如1/e²或半高宽）处的两条边界光线之间的夹角。它是评估激光、LED等光源方向性和能量集中度的重要指标，直接影响光学系统的设计（如聚焦、准直）和应用效果（如通信、加工、测量）。

4.1、发散角的定义与物理意义

定义：
- 数学表达：对于旋转对称光束（如高斯光束），发散角 θ 是光束在远场（z→∞）时，光强下降至中心最大值 I0 的 1/e2（约13.5%）处的半角宽度，即：

θ=z→∞limzw(z)

其中 $w(z)$ 是光束在距离 $z$ 处的半径。

几何意义：发散角越小，光束传播越接近平行，方向性越好；发散角越大，光束扩散越快。

物理意义：
- 能量集中度：发散角小意味着能量更集中于主瓣，适用于远距离传输（如激光通信、测距）。
- 系统设计约束：发散角限制了光学元件（如透镜、反射镜）的最小尺寸和焦距选择。
- 应用适配性：不同应用对发散角要求不同（如激光加工需小发散角实现精细聚焦，照明需大发散角实现均匀覆盖）。

4.2、发散角的理论模型与计算

1. 高斯光束（TEM₀₀模）

数学表达式：
高斯光束的发散角由束腰半径 w0 和波长 λ 决定：

θ=πw0λ

其中：

λ 为光波波长，
w0 为光束束腰半径（光强最大处半径）。
特点：
- 发散角与束腰半径成反比：束腰越细，发散角越大。
- 理论最小发散角受衍射极限约束（即无法通过缩小束腰无限减小发散角）。

2. 平顶光束（Top-Hat Profile）

数学表达式：
平顶光束的发散角需通过傅里叶变换或远场衍射理论计算。近似情况下，若光束直径为 D，则发散角可表示为：

θ≈Dλ

（与高斯光束类似，但系数可能因边缘锐度不同而变化）。

特点：
- 平顶光束的发散角通常略大于高斯光束（因边缘锐截止导致高频成分更多）。

3. 多模光束

数学表达式：
多模光束的发散角由模式混合决定，通常大于单模光束。例如，对于厄米-高斯模（TEMₘₙ），发散角可表示为：

θm,n=θ01+(2m+n)2

其中 θ0 为基模（TEM₀₀）发散角。

特点：
- 高阶模（m+n 越大）发散角越大，光束质量越差。

4.3、发散角的测量方法

1. 远场法（直接测量法）

原理：
在足够远的距离 z 处（满足 z≫πw02/λ），测量光束半径 w(z)，通过 θ≈w(z)/z 计算发散角。
步骤：
1. 固定激光器，在远场放置光屏或CCD相机。
2. 测量光束直径 D(z)（如通过刀口法或图像处理）。
3. 计算发散角：

θ=2zD(z)

优点：
- 简单直接，适用于低功率光束。
缺点：
- 需足够大的测量距离（实验室空间受限时难以实现）。
- 高功率光束可能损坏探测器。

2. 近场法（通过束腰与波长计算）

原理：
利用高斯光束发散角公式 θ=λ/(πw0)，通过测量束腰半径 w0 和波长 λ 计算发散角。
步骤：
1. 用CCD或扫描探针测量光束近场强度分布，拟合高斯曲线得到 w0。
2. 已知波长 λ（如通过波长计测量），代入公式计算 θ。
优点：
- 无需远场测量，节省空间。
缺点：
- 仅适用于高斯或近似高斯光束。
- 束腰测量精度受探针分辨率限制。

3. 干涉法（高精度测量）

原理：
利用干涉仪（如马赫-曾德尔干涉仪）测量光束的波前曲率，反推发散角。
步骤：
1. 将光束分为两束，一束直接传播，另一束经反射镜引入路径差。
2. 调整路径差使两束光干涉，观察干涉条纹弯曲程度。
3. 通过条纹弯曲量计算波前曲率，进而得到发散角。
优点：
- 精度高（可达亚毫弧度级）。
缺点：
- 系统复杂，需精密光学元件。
- 对环境振动敏感。

4.4、影响发散角的因素

光束模式：
- 单模光束（TEM₀₀）发散角最小，多模光束发散角随模式阶数增加而增大。
光学元件像差：
- 透镜的球差、色差会破坏光束波前，导致发散角增大。
- 自适应光学可校正像差，优化发散角。
非线性效应：
- 高功率下，克尔效应或自聚焦效应可能改变光束发散角（如光束自收缩导致发散角减小）。
热效应：
- 光学元件受热变形（如激光晶体热透镜效应）会改变光束参数，影响发散角。

4.5、发散角的应用场景与优化

1. 激光通信

需求：小发散角（<1 mrad）实现远距离传输（如卫星间通信）。
优化方法：
- 使用单模光纤输出高斯光束。
- 在发射端加入准直透镜（如非球面透镜）压缩发散角。

2. 激光加工

需求：适中发散角（1-10 mrad）平衡聚焦深度与能量密度。
优化方法：
- 选择多模激光器（如CO₂激光器）获得较大发散角，适应粗糙表面加工。
- 使用变焦光束扩束器动态调整发散角。

3. 光学测量

需求：极小发散角（<0.1 mrad）提高干涉仪分辨率。
优化方法：
- 使用超稳腔激光器（如He-Ne稳频激光器）输出低发散角光束。
- 在测量系统中加入空间滤波器（如针孔滤波）净化光束模式。

4.6、实际案例：高斯光束发散角的测量与验证

案例1：He-Ne激光器（632.8 nm）发散角测量

测量步骤：
1. 用CCD测量近场光束强度分布，拟合高斯曲线得束腰半径 w0=150μm。
2. 已知波长 λ=632.8nm，计算理论发散角：

θ=πw0λ=π×150×10−6632.8×10−9≈1.35mrad

在远场（z=10m）测量光束直径 D=2.7cm，计算实验发散角：

θexp=2zD=2×100.027=1.35mrad

结论：
理论与实验结果一致，验证高斯光束发散角公式。

案例2：光纤激光器发散角优化

问题：
多模光纤激光器输出光束发散角过大（θ=10mrad），导致聚焦光斑尺寸大（d=100μm），无法满足微加工需求。
优化方案：
1. 在光纤输出端熔接单模光纤（模式滤波），将光束转换为近似高斯分布。
2. 加入准直透镜（焦距 f=100mm），压缩发散角至 θ′=1mrad。
3. 聚焦后光斑尺寸减小至 d′=10μm，满足加工要求。
效果：
发散角降低10倍，聚焦光斑尺寸缩小10倍，加工精度显著提升。

五、核心功能 - M²因子

M²因子：量化光束质量，定义为实际光束与理想高斯光束的发散角与束腰直径乘积之比（M²≥1，越接近1表示光束质量越好）。

M²因子（光束质量因子）是激光领域用于量化激光光束质量的核心参数，定义为实际光束参数乘积（BPP）与理想基模高斯光束参数乘积的比值，其数值综合反映了光束的发散程度、聚焦性能及传输稳定性。以下是关键要点解析：

5.1、数学定义与物理意义

波长越大，束腰半径越大；束腰半径越大，发散性越大。
波长越大，发散角越大；发散角越大，发散性越大。
束腰半径越小，发散角越大；反之，束腰半径越大，发散角越小。

5.2、测量方法与标准

ISO标准方法：
- 步骤：
  1. 使用高光学质量透镜聚焦激光束。
  2. 在束腰附近（5个位置）和远场（距离束腰至少一个瑞利长度的5个位置）测量光束宽度（D4σ法）。
  3. 将10个测量数据拟合到双曲线模型，计算 M2 值。
- 意义：确保测量结果的一致性和准确性，避免操作误差。
常用测量技术：
- 相机式直接测量法：
  - 设备：光束质量分析仪（如OPHIR BSQ-SP204S）。
  - 优点：测量速度快（1分钟内完成），精度高。
  - 局限：需光路衰减，无法直接测量1100nm以上波长。
- 狭缝扫描式测量法：
  - 设备：狭缝扫描仪（如OPHIR NANOSCAN系列）。
  - 优点：成本低，可直接测量高功率激光器，兼容多波长。
  - 局限：搭建复杂，测量速度慢，对操作技能要求高。
- 相位测量法：
  - 设备：波前传感器（如Phasics SID4系列）。
  - 优点：直接测量波前相位，精度高，适用于复杂光束。
  - 局限：设备成本较高。

5.3、影响因素与优化策略

影响因素：
- 光学元件缺陷：如透镜像差、表面粗糙度。
- 谐振腔设计：腔长、反射镜形状及材料质量。
- 环境因素：温度波动、空气流动、振动。
- 激光模式：多模光束的 M2 值显著高于单模。
优化策略：
- 元件优化：采用高精度光学加工技术，减少表面缺陷。
- 谐振腔改进：延长腔长、优化反射镜形状，提升模式稳定性。
- 环境控制：恒温恒湿、减震隔离，降低外部干扰。
- 模式选择：通过空间滤波或模式选择器抑制高阶模。

5.4、应用场景与工程价值

工业加工：
- 激光切割/焊接：M2 值越小，聚焦光斑越小，热影响区越窄，加工精度越高。例如，M2<1.2 的激光器适用于精密微加工。
- 3D打印：高光束质量（M2≈1）可实现层间高分辨率融合。
光学通信：
- 光纤耦合：单模光纤要求 M2≤1.1，以降低耦合损耗。
- 自由空间传输：低 M2 值可减少大气湍流引起的光束畸变。
激光雷达：
- 测距精度：M2 值越小，光束发散角越小，测距分辨率越高。
- 探测灵敏度：高光束质量可提升回波信号信噪比。
科研领域：
- 超快激光：M2 值影响脉冲时空耦合特性，需优化至接近衍射极限。
- 冷原子实验：高斯光束质量（M2≈1）是实现原子囚禁的关键条件。

5.5、局限性与发展趋势

局限性：
- 高能激光：非稳腔输出的离散能量分布光束可能导致 M2 计算误差超过20%。
- 超快脉冲：时空耦合效应可能使 M2 无法全面描述光束质量。
发展趋势：
- 多参数综合评价：结合环围能量比（BQ值）、斯特列尔比（S）等参数，构建更全面的光束质量评估体系。
- 智能化测量：利用机器学习算法自动优化测量参数，提升数据拟合效率。
- 新型激光器设计：通过拓扑优化谐振腔结构，实现 M2≈1 的高功率激光输出。

六、波长、发散角、束腰半径、发散性的关系

波长、发散角、束腰半径和发散性是描述激光光束传播特性的核心参数，它们之间通过衍射理论和几何光学紧密关联。以下是它们之间关系的系统性解析：

6.1、核心参数定义与物理意义

波长（λ）：
- 定义：激光的电磁波波长，决定光束的衍射特性。
- 影响：波长越短，衍射效应越弱，光束可聚焦得更细；波长越长，衍射效应越强，光束发散角越大。
束腰半径（ω₀）：
- 定义：光束横截面上光强最大处（束腰）的半径，通常指1/e²强度点。
- 影响：束腰半径越小，光束聚焦能力越强，但发散角越大；束腰半径越大，光束准直性越好，但聚焦光斑尺寸受限。
发散角（θ）：
- 定义：光束远场（距离束腰足够远）的传播角度，通常指半角全宽（FWHM）或1/e²强度角。
- 影响：发散角越小，光束传播距离越远；发散角越大，光束能量扩散越快。
发散性：
- 广义定义：光束在传播过程中扩散的能力，由发散角和光束能量分布共同决定。
- 量化指标：常用发散角、光束参数乘积（BPP）或M²因子（光束质量因子）表征。

6.2、数学关系：高斯光束理论

对于理想基模高斯光束（M²=1），参数间关系由以下公式描述：

发散角与束腰半径的关系：

θ=πω0λ

物理意义：发散角与波长成正比，与束腰半径成反比。束腰越小，发散角越大；波长越长，发散角越大。

光束参数乘积（BPP）：

BPP=ω0⋅θ=πλ

意义：BPP是衍射极限的标志，实际光束的BPP均大于或等于此值（M² ≥ 1）。

M²因子与发散性的关系：

M2=理想高斯光束的BPP实际光束的BPP=λ/πω0⋅θ实际

意义：M²因子综合反映了光束的发散性。M²=1表示衍射极限光束，M²>1表示光束质量下降，发散性增强。

6.3、参数间的相互影响与权衡

波长与发散角、束腰半径的权衡：
- 短波长激光（如紫外、可见光）：
  - 优势：衍射极限小，可聚焦到更细的光斑（如激光微加工）。
  - 局限：材料吸收率高，可能引发热损伤；大气散射较强（如紫外激光在空气中衰减快）。
- 长波长激光（如红外、CO₂激光）：
  - 优势：衍射极限大，光束发散角较小，适合长距离传输（如激光通信）。
  - 局限：聚焦光斑较大，功率密度受限。
束腰半径与发散角的权衡：
- 小束腰半径：
  - 优势：聚焦光斑小，功率密度高（如激光切割）。
  - 局限：发散角大，传播距离短；对光学元件像差敏感。
- 大束腰半径：
  - 优势：发散角小，传播距离远（如激光雷达准直）。
  - 局限：聚焦光斑大，功率密度低。
发散性与光束质量的关系：
- 高光束质量（M²≈1）：
  - 特征：发散角接近衍射极限，光束能量集中。
  - 应用：精密加工、光学通信、冷原子实验。
- 低光束质量（M²≫1）：
  - 特征：发散角大，光束能量分散。
  - 应用：高功率焊接、材料表面处理（需大光斑覆盖）。

6.4、实际应用中的优化策略

激光加工：
- 需求：高功率密度（小光斑）与低发散角（长焦深）的平衡。
- 策略：
  - 选择短波长激光（如光纤激光器1.06μm）以减小衍射极限。
  - 通过透镜聚焦调整束腰半径，但需考虑热透镜效应（高功率下透镜材料变形导致ω₀变化）。
  - 使用空间滤波器抑制高阶模，降低M²因子。
光学通信：
- 需求：低发散角（长距离传输）与小模场直径（单模光纤耦合）的平衡。
- 策略：
  - 采用单模光纤（模场直径约5-10μm），限制光束为基模高斯分布。
  - 通过准直器（大束腰半径）减小发散角，但需权衡系统体积。
  - 选择1.55μm波长（低损耗窗口）以优化传输距离。
激光雷达：
- 需求：高分辨率（小发散角）与大探测范围（高功率）的平衡。
- 策略：
  - 采用短脉冲激光（如1550nm光纤激光器）结合小束腰设计以减小发散角。
  - 使用波长更短的激光（如532nm绿光）可进一步提升分辨率，但受大气散射限制。
  - 通过光束整形技术（如贝塞尔光束）扩展焦深，降低对发散角的依赖。

6.5、常见误区与澄清

误区1：束腰半径越小，光束质量越好。
- 澄清：光束质量由M²因子决定。仅缩小束腰半径可能增加发散角，导致M²恶化（如多模光束）。需同时优化模式纯度。
误区2：波长越短，发散性越弱。
- 澄清：波长影响衍射极限，但发散性还受M²因子、光束能量分布等因素影响。短波长激光若存在高阶模，发散性可能更强。
误区3：发散角可无限缩小。
- 澄清：受衍射极限约束，发散角最小值为θ_min = λ/(πω₀)。实际光束因M²>1，发散角更大。

6.6、参数关系总结表

参数	与发散角的关系	与束腰半径的关系	与波长的关系	对发散性的影响
波长（λ）	正比（λ↑→θ↑）	无直接关系（通过θ间接影响）	基础参数，决定衍射极限	波长越长，发散性越强
束腰半径（ω₀）	反比（ω₀↓→θ↑）	基础参数，决定聚焦能力	无直接关系（通过θ间接影响）	束腰越小，发散性越强
发散角（θ）	基础参数，表征发散性	反比关系（θ↑→ω₀↓）	正比关系（θ↑→λ↑）	发散角越大，发散性越强
M²因子	正比（M²↑→θ_实际↑）	正比（M²↑→ω₀·θ↑）	无直接关系（通过θ间接影响）	M²越大，发散性越强（光束质量越差）

七、光束指向性

光束指向性（Beam Pointing Stability）是衡量激光光束在传播过程中方向稳定性的关键参数，直接决定了激光系统在精密加工、光学测量、通信等领域的性能上限。其核心指标包括指向稳定性（短时间抖动）和指向漂移（长时间偏移），通常以角秒（arcsec）或微弧度（μrad）为单位量化。

7.1、光束指向性的物理本质

光束指向性由激光光源、光学系统及环境干扰共同决定，其物理机制可归纳为以下三方面：

光源内在因素
- 腔模畸变：激光谐振腔内增益介质不均匀、热透镜效应或机械振动会导致腔模变形，使输出光束方向偏移。
- 模式竞争：多纵模或横模竞争可能引发光强分布变化，间接影响光束方向。
- 泵浦源噪声：如半导体激光器的电流波动会通过热效应传递至光束方向。
光学系统误差
- 元件缺陷：透镜、反射镜的面形误差（如PV值超标）会引入波前畸变，导致光束偏折。
- 装调误差：光学元件的倾斜、偏心或轴向位移会破坏光路共轴性，引发指向偏移。
- 材料热变形：高功率激光下，光学元件因吸收热量产生热应力，导致面形变化（如透镜弯曲）。
环境干扰
- 机械振动：外部振动通过光学平台传递至光学元件，引发微小位移。
- 温度波动：材料热胀冷缩导致光学元件位置或角度变化。
- 空气湍流：室内气流或户外风场引起折射率分布不均，使光束路径弯曲。

7.2、光束指向性的量化指标

指向稳定性（Pointing Jitter）
- 定义：短时间（毫秒至秒级）内光束方向的随机波动。
- 测量：通过四象限探测器（QPD）或位置敏感探测器（PSD）实时监测光斑位置，计算标准差。
- 典型值：高精度激光系统需达到亚微弧度（<0.1 μrad）级别。
指向漂移（Pointing Drift）
- 定义：长时间（分钟至小时级）内光束方向的缓慢偏移。
- 测量：通过长期监测光斑位置变化，拟合漂移速率。
- 典型值：工业级激光器允许漂移<10 μrad/h，科研级需<1 μrad/h。
指向重复性（Pointing Repeatability）
- 定义：多次开关机或循环测试后，光束方向的一致性。
- 测量：记录多次启动后的光斑位置，计算最大偏差。

7.3、提升光束指向性的关键技术

光源优化
- 单频稳频激光器：采用PDH（Pound-Drever-Hall）技术锁定激光频率，抑制模式竞争。
- 低噪声泵浦源：使用恒流驱动或温度控制降低半导体激光器噪声。
- 热管理：通过水冷或TEC（热电制冷）控制增益介质温度，减少热透镜效应。
光学系统设计
- 轻量化镜架：采用碳纤维或铟钢材料，降低热膨胀系数。
- 主动补偿：集成压电陶瓷（PZT）或音圈电机，实时调整镜片角度。
- 离轴设计：避免直通光路中元件热变形对光束的影响。
环境隔离
- 隔振台：使用空气弹簧或主动隔振系统隔离机械振动。
- 恒温腔：将光学系统置于恒温环境中，控制温度波动<0.1℃。
- 密封罩：对光学元件进行密封，防止气流扰动。
闭环控制
- 反馈系统：通过QPD监测光斑位置，驱动PZT或快速转向镜（FSM）实时校正。
- 前馈控制：结合加速度计或温度传感器预测干扰，提前补偿。

7.4、典型应用场景与需求

半导体光刻
- 需求：EUV光刻机需光束指向稳定性<0.1 μrad，以确保掩模版与晶圆对准精度。
- 方案：采用主动隔振+闭环控制，结合高刚性光学平台。
引力波探测
- 需求：LIGO等装置要求光束指向漂移<1 nrad/√Hz（中频段），以检测时空微小扭曲。
- 方案：超低噪声激光器+多层隔振+真空环境。
激光雷达（LiDAR）
- 需求：自动驾驶LiDAR需指向重复性<10 μrad，以保证测距准确性。
- 方案：MEMS微镜扫描+温度补偿算法。
精密加工
- 需求：深紫外激光切割需指向稳定性<1 μrad，以避免加工边缘毛刺。
- 方案：闭环控制+防潮封装（如CLBO晶体系统）。