一、题目解析
1、只包含0、1的二进制数组
2、找到含有相同数量的0和1，并返回其子数组长度
二、算法原理
解法1：暴力枚举 时间复杂度O(N^2)
解法2：前缀和+哈希表
对于统计子数组中的0和1的数量有点困难，我们可以将其转化一下
转化：
1、将所有的0变为-1
2、在数组中，找出最长子数组，使子数组中所有元素的和为0
将问题转化后，大体思路与560.和为k的子数组差不多，但还有细节问题问题需要处理，建议先去自己尝试一下，实在不行再来观看细节问题
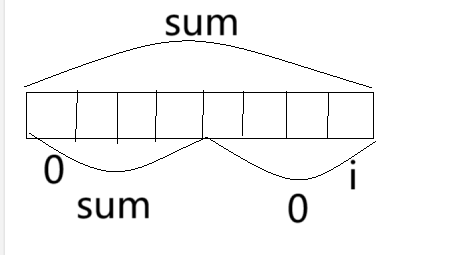
细节问题：
1、哈希表中存什么？
在和为k的子数组中，unordered_map<int，int> hash，第一int存的是前缀和，第二个int存的前缀和出现的频率，而在本题中，所求的是子数组的长度，所以第一个int存的也是前缀和，第二个int存的是下标
2、什么时候存入哈希表？
在判断条件结束后，就可以丢进哈希表中
3、如果有重复的<sum，i>该怎么处理？
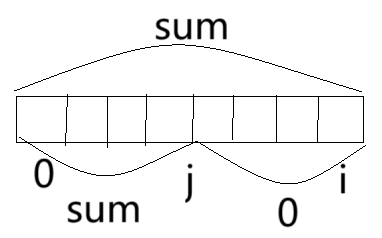
对于前缀和同样都为sum的两个结果，j比i要靠左一点，要想长度越长，左边的长度必然是最短的，所以对于重复的<sum，i>只保留前面或者最左边的那一对<sum，i>
4、 默认前缀和为0的hash[0]，怎么存储？
为了避免[0,i-1]的所有元素前缀为0的情况遗漏，在560.和为k的子数组中，我们要在[-1,0]中找到前缀和为0的数组，便将hash[0]的值设置为1，但在该题中计算的是长度，所以hash[0]的值设置为-1
5、长度怎么计算？
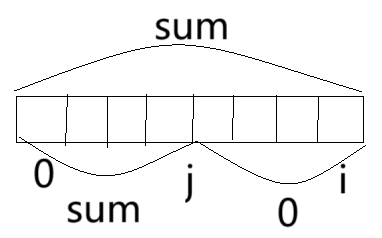
由于计算的长度不会包括j元素，所以长度为i-j，这里的j是hash表中存的下标
三、代码示例
解法2：
class Solution {
public:int findMaxLength(vector<int>& nums){//将数组中所有0变为-1for(auto& e : nums){if(e == 0) e = -1;}//找一段和为0的最长子数组int ret = 0,sum = 0;unordered_map<int,int> hash;hash[0] = -1;for(int i = 0;i<nums.size();i++){sum += nums[i];if(hash.count(sum)) ret = max(ret,i-hash[sum]);else hash[sum] = i;}return ret;}
};
