RayS：一种用于硬标签对抗攻击的光线搜索方法

Jinghui Chen
University of California, Los Angeles
jhchen@cs.ucla.edu
Quanquan Gu
University of California, Los Angeles
qgu@cs.ucla.edu
原文链接：https://arxiv.org/pdf/2006.12792

摘要

深度神经网络（DNNs）易受对抗攻击。在不同的攻击设置中，最具挑战性但也最实用的是硬标签设置（hard-label setting），其中攻击者只能访问目标模型的硬标签输出（预测标签）。在广泛使用的 (L_{\infty}) 范数威胁模型下，之前的尝试在攻击成功率方面不够有效，在查询复杂度方面也不够高效。本文中，我们提出了光线搜索攻击（Ray Searching attack, RayS），它极大地提高了硬标签攻击的有效性和效率。与之前的工作不同，我们将寻找最近决策边界的连续问题重新表述为一个离散问题，该问题不需要任何零阶梯度估计。同时，通过一个快速检查步骤（fast check step）消除了所有不必要的搜索。这显著减少了我们的硬标签攻击所需的查询次数。此外，有趣的是，我们发现所提出的 RayS 攻击也可以用作检测可能的“虚假鲁棒”（falsely robust）模型的健全性检查（sanity check）。在几个最近提出的声称达到最先进（state-of-the-art）鲁棒精度的防御方法上，我们的攻击方法表明，当前的白盒/黑盒攻击可能仍然会给人一种错误的安全感，最流行的 PGD 攻击与 RayS 攻击之间的鲁棒精度下降可能高达 28%。我们相信，我们提出的 RayS 攻击可以帮助识别那些击败了大多数白盒/黑盒攻击的虚假鲁棒模型。

关键词: 鲁棒性 (robustness), 深度神经网络 (deep neural networks), 硬标签攻击 (hard-label attacks)

CCS 概念: • 计算理论 → 机器学习理论；• 计算方法学 → 离散空间搜索；目标识别

1. 引言

在过去十年中，深度神经网络（DNNs）在计算机视觉[15, 36]和语音识别[17]等许多机器学习任务上取得了显著成功。尽管取得了巨大成功，但最近的研究表明 DNNs 容易受到对抗样本（adversarial examples）的攻击，即即使人眼不可察觉的（专门设计而非随机的）扰动也可能导致最先进的分类器做出错误预测[13, 38]。这种有趣的现象很快引发了对抗攻击[3, 5, 7]（试图用这种微小扰动破坏 DNN 模型）与对抗防御方法[27, 33, 40, 41, 46]（试图防御现有攻击）之间的军备竞赛。在这场军备竞赛中，许多启发式防御方法[12, 14, 26, 33, 34, 35, 42]后来被证明在更强大的攻击下无效。一个例外是对抗训练（adversarial training）[13, 27]，它被证明是一种有效的防御方法。

在这场军备竞赛中，人们提出了大量的对抗攻击方法。根据攻击者可以访问的信息量不同，对抗攻击通常分为三类：白盒攻击（white-box attacks）、黑盒攻击（black-box attacks）和硬标签攻击（hard-label attacks）。白盒攻击[5, 27]是指攻击者可以访问有关目标模型的所有信息，包括模型权重、结构、参数以及可能的防御机制。由于白盒攻击者可以访问所有模型细节，它可以高效地在目标模型上执行反向传播并计算梯度。在黑盒攻击中，攻击者只能访问目标模型的查询软标签输出（不同类别的 logits 或概率分布），其他部分被视为黑盒。与白盒情况相比，黑盒设置实用得多，然而，在这种设置下，攻击者无法执行反向传播和直接梯度计算。因此，许多人转向从已知模型迁移梯度[30]或通过零阶优化方法（zeroth-order optimization methods）估计真实梯度[1, 7, 19, 20]。

另一方面，硬标签攻击（hard-label attacks），也称为基于决策的攻击（decision-based attacks），只允许攻击者查询目标模型并获得硬标签输出（预测标签）。显然，硬标签设置是最具挑战性的，但也是最实用的，因为在现实中，攻击者事先知道目标模型的所有信息或获得所有类别的概率预测的可能性很小。仅能访问硬标签也意味着攻击者无法辨别在输入一个轻微扰动的输入样本时（假设这种轻微扰动不会改变模型预测），目标模型输出的细微变化。因此，攻击者只能在目标模型的决策边界（decision boundary）附近找到信息线索，在那里微小的扰动可能导致模型产生不同的预测标签。之前的工作[4, 6, 9, 10]大多遵循这一思路来解决硬标签对抗攻击问题。然而，[4, 6, 9, 10] 最初都是针对 $L_2$ 范数威胁模型提出的，而 $L_{\infty }$ 范数威胁模型[21, 27, 44, 45, 46]目前是最流行和广泛使用的。尽管[6, 9, 10]提供了对 $L_{\infty }$ 范数情况的扩展，但没有一个是为 $L_{\infty }$ 范数情况优化的，因此，它们的攻击性能在很大程度上落后于传统的基于 $L_{\infty }$ 范数的白盒和黑盒攻击，使得

它们在现实世界场景中不适用。这就引出了一个自然的问题：

我们能否设计一种硬标签攻击，能够极大地改进之前的硬标签攻击，并为最广泛使用的 $L_{\infty }$范数威胁模型提供实用的攻击？

在本文中，我们肯定地回答了这个问题。我们将我们的主要贡献总结如下：

• 我们提出了光线搜索攻击（Ray Searching attack），它仅依赖于目标模型的硬标签输出。我们表明，在 $L_{\infty }$ 范数威胁模型下，所提出的硬标签攻击比之前的硬标签攻击更有效和高效。
• 与之前大多数通过零阶优化方法解决硬标签攻击问题的工作不同，我们将寻找最近决策边界的连续优化问题重新表述为一个离散问题，并直接在一组离散的光线方向（ray directions）上搜索最近的决策边界。还利用一个快速检查步骤来跳过不必要的搜索。这显著节省了硬标签攻击所需的查询次数。我们提出的攻击也不需要调整超参数，如步长或有限差分常数，使其非常稳定且易于应用。
• 此外，我们提出的 RayS 攻击也可以用作一种强大的攻击来检测可能的“虚假鲁棒”模型。通过用 RayS 攻击评估几个最近提出的声称达到最先进鲁棒精度的防御方法，我们表明当前的白盒/黑盒攻击可能会被欺骗，给人一种错误的安全感。具体来说，RayS 攻击显著降低了最流行的 PGD 攻击在几个鲁棒模型上的鲁棒精度，差异可能高达 28%。我们相信，我们提出的 RayS 攻击可以帮助识别那些欺骗当前白盒/黑盒攻击的虚假鲁棒模型。

本文的其余部分组织如下：在第 2 节中，我们简要回顾了关于对抗攻击的现有文献。我们在第 3 节中介绍我们提出的光线搜索攻击（RayS）。在第 4 节中，我们通过评估几个最近提出的防御方法，展示了所提出的 RayS 攻击比其他硬标签攻击更高效，并且可以用作检测虚假鲁棒模型的健全性检查。最后，我们在第 5 节总结本文并提供讨论。

符号说明。 对于一个 $d$ 维向量 $\mathbf{x}=[{\mathbf{x}}_1,...,{\mathbf{x}}_d{]}^{\top }$，我们使用∥x∥0=∑i1{xi≠0}\|\mathbf{x}\|_{0}=\sum_{i}1\{\mathbf{x}_{i}\neq 0\}∥x∥0​=∑i​1{xi​=0}表示其 ${\ell }_0$-范数，使用$\Vert \mathbf{x}{\Vert }_2=({\sum }_{l=1}^d|{\mathbf{x}}_l{|}^2{)}^{1/2}$ 表示其 ${\ell }_2$-范数，使用 $\Vert \mathbf{x}{\Vert }_{\infty }={\max }_i|{\mathbf{x}}_l|$ 表示其${\ell }_{\infty }$-范数，其中 $1(\cdot )$ 表示指示函数。

2. 相关工作

有大量关于评估模型鲁棒性和生成对抗样本的工作。在本节中，我们回顾与我们的工作最相关的工作。

白盒攻击： Szegedy 等人 [38] 首先提出了对抗样本的概念，并采用 L-BFGS 算法进行攻击。Goodfellow 等人 [13] 通过线性化网络损失函数提出了快速梯度符号法（Fast Gradient Sign Method, FGSM）。Kurakin 等人 [23] 提出迭代执行 FGSM 然后进行投影，这等价于投影梯度下降（Projected Gradient Descent, PGD）[27]。Papernot 等人 [32] 提出了基于 Jacobian 显著图（Jacobian saliency map）的 JSMA 方法。Moosavi-Dezfooli 等人 [29] 通过将数据投影到最近的分离超平面提出了 DeepFool 攻击。Carlini 和 Wagner [5] 引入了基于边界损失函数（margin-based loss function）的 CW 攻击，并表明防御性蒸馏（defensive distillation）[33] 并非真正鲁棒。Chen 等人 [7] 提出了一种基于 Frank-Wolfe 方法和动量的无投影攻击（projection-free attack）。Athalye 等人 [3] 指出了混淆梯度（obfuscated gradients）的影响，并提出了 BPDA 攻击来打破那些混淆梯度的防御。

黑盒攻击： 除了上述白盒攻击算法外，还有大量文献[18, 18, 19, 20, 31, 7, 8, 25]关注黑盒攻击情况，其中信息仅限于模型的 logits 输出，而不是模型的每个细节。基于迁移的黑盒攻击[31, 30, 18]试图将梯度从已知模型迁移到黑盒目标模型，然后应用与白盒情况相同的技术。然而，它们的攻击效果通常不太令人满意。基于优化的黑盒攻击旨在通过零阶优化方法估计真实梯度。Chen 等人 [8] 提出通过对每个维度进行有限差分（finite-difference）来估计梯度。Ilyas 等人 [19] 提出通过自然进化策略（Natural Evolutionary Strategies）改进 [8] 的查询效率。Ilyas 等人 [20] 通过利用梯度先验（gradient priors）进一步改进了 [19]。Uesato 等人 [39] 提出使用 SPSA 方法构建一种无梯度攻击（gradient-free attack），可以打破梯度消失防御（vanishing gradient defenses）。Al-Dujaili 和 O’Reilly [1] 提出直接估计梯度的符号而不是真实梯度本身。Moon 等人 [28] 将连续优化问题重新表述为离散问题，并提出了一种基于组合搜索（combinatorial search）的算法以提高攻击效率。Andriushchenko 等人 [2] 提出了一种随机搜索方案，迭代地将小方块（squares）修补（patch）到测试样本上。

硬标签攻击： Brendel 等人 [4] 首先研究了硬标签攻击问题，并提议通过在决策边界附近进行随机游走（random walks）来解决。Ilyas 等人 [19] 展示了一种将硬标签攻击问题转化为软标签攻击问题的方法。Cheng 等人 [9] 将对偶优化问题转化为寻找导致到决策边界距离最短（$L_2$ 距离）的最佳方向的问题，并通过零阶优化方法优化这个新问题。Cheng 等人 [10] 通过估计梯度符号而不是真实梯度，进一步改进了 [9] 的查询复杂度。Chen 等人 [6] 也应用零阶符号预言机（zeroth-order sign oracle）来改进 [4]，通过搜索步长并保持迭代点沿决策边界移动。

3. 提出的方法

在本节中，我们介绍我们提出的光线搜索攻击（Ray Searching attack, RayS）。在我们详细介绍我们提出的方法之前，我们首先概述一下之前的对抗攻击问题表述。

3.1 先前问题表述概述

我们用 $f$ 表示 DNN 模型，测试数据样本为 {x,y}\{\mathbf{x},y\}{x,y}。对抗攻击的目标是解决以下优化

问题：
min⁡x′1{f(x′)=y}s.t., ∥x′−x∥∞≤ϵ,(3.1)\min_{\mathbf{x}^{\prime}}\mathbb{1}\{f(\mathbf{x}^{\prime})=y\} \text{ s.t., }\|\mathbf{x}^{\prime}-\mathbf{x}\|_{\infty}\leq\epsilon,\quad (3.1)x′min​1{f(x′)=y} s.t., ∥x′−x∥∞​≤ϵ,(3.1)
其中 $ϵ$ 表示允许的最大扰动强度。指示函数 1{f(x′)=y}\mathbb{1}\{f(\mathbf{x}^{\prime})=y\}1{f(x′)=y} 难以优化，因此，[1, 7, 19, 20, 27, 46] 将 (3.1) 松弛为：
$$\underset{{\mathbf{x}}^{\prime }}{\max }\ell (f({\mathbf{x}}^{\prime }),y)\text{ s.t., }\Vert {\mathbf{x}}^{\prime }-\mathbf{x}{\Vert }_{\infty }\le ϵ,(3.2)$$
其中 $\ell$ 表示替代损失函数（surrogate loss function），例如交叉熵损失（CrossEntropy loss）。另一方面，传统的硬标签攻击 [9, 10] 将 (3.1) 重新表述为：
min⁡dg(d)其中 g(d)=argmin⁡r1{f(x+rd/∥d∥2)≠y}.(3.3)\min_{\mathbf{d}}g(\mathbf{d})\text{ 其中 }\;g(\mathbf{d})=\operatorname*{argmin}_{r}\mathbb{1}\{f(\mathbf{x}+r\mathbf{d}/\|\mathbf{d}\|_{2})\neq y\}.\quad (3.3)dmin​g(d) 其中 g(d)=rargmin​1{f(x+rd/∥d∥2​)=y}.(3.3)
这里 $g(\mathbf{d})$ 表示从原始样本 $\mathbf{x}$ 沿光线方向 $\mathbf{d}$ 到决策边界的半径（decision boundary radius），目标是找到关于原始样本 $\mathbf{x}$ 的最小决策边界半径。令 $(\hat{r},\hat{\mathbf{d}})$ 表示最小决策边界半径及其对应的光线方向。如果最小决策边界半径满足 $|\hat{r}\hat{\mathbf{d}}/\Vert \hat{\mathbf{d}}{\Vert }_2{\Vert }_{\infty }\le ϵ$，它将被计为一次成功的攻击。

虽然之前的工作 [9, 10] 试图通过零阶优化方法估计 $g(\mathbf{d})$ 的梯度以连续方式解决问题 (3.3)，但仅能访问硬标签的限制给解决 (3.3) 带来了巨大挑战。具体来说，估计决策边界半径 $g(\mathbf{d})$ 通常需要一个二分搜索过程，而通过有限差分（finite difference）估计 $g(\mathbf{d})$的信息梯度需要多轮 $g(\mathbf{d})$ 计算。此外，由于零阶梯度估计过程中的方差很大，优化 (3.3) 通常需要大量的梯度步骤。这些因素加在一起，使得解决 (3.3) 比黑盒攻击效率低得多，更不用说白盒攻击了。

鉴于上述所有问题，我们转向直接搜索最近的决策边界，而无需估计任何梯度。

3.2 光线搜索方向

在有限次查询下，不可能搜索整个连续的光线方向空间。因此，我们需要将搜索空间限制在一个离散的光线方向集合上，以使直接搜索成为可能。请注意，对 (3.2) 应用 FGSM 会在 $L_{\infty }$ 范数球的顶点（vertex）处产生最优解 [7, 28]，这表明这些顶点可能为 (3.2) 提供可能的解。 [28] 中的经验发现也表明，从 PGD 攻击获得的 (3.2) 的解大多位于 $L_{\infty }$ 范数球的顶点上。受此启发，Moon 等人 [28] 将可行解集限制为 $L_{\infty }$ 范数球的顶点。遵循这一思路，由于我们的目标是获得决策边界半径，我们考虑指向 $L_{\infty }$ 范数球顶点的光线方向，即 d∈{−1,1}d\mathbf{d}\in\{-1,1\}^{d}d∈{−1,1}d，其中 $d$ 表示原始数据样本${\mathbf{x}}^{†}$ 的维度。因此，我们不解决 (3.3)，而是转向解决一个离散问题：
min⁡d∈{−1,1}dg(d)其中 g(d)=argmin⁡r1{f(x+rd/∥d∥2)≠y}.(3.4)\min_{\mathbf{d}\in\{-1,1\}^{d}}g(\mathbf{d})\text{ 其中 }\;g(\mathbf{d})=\operatorname*{argmin}_{r}\mathbb{1}\{f(\mathbf{x}+r\mathbf{d}/\|\mathbf{d}\|_{2})\neq y\}.\quad (3.4)d∈{−1,1}dmin​g(d) 其中 g(d)=rargmin​1{f(x+rd/∥d∥2​)=y}.(3.4)
在问题 (3.4) 中，我们将搜索空间从 ${\mathbb{R}}^d$ 减少到 {−1,1}d\{-1,1\}^{d}{−1,1}d，它包含 $2^d$ 个可能的搜索方向。

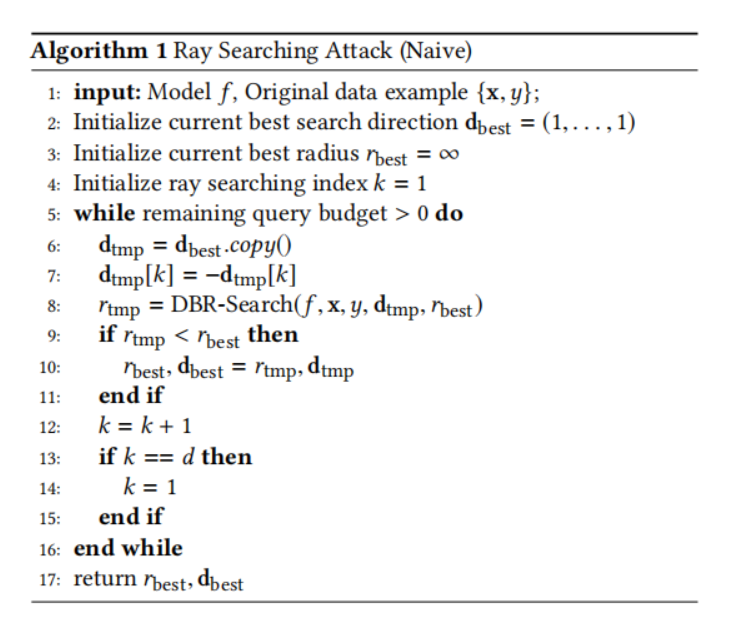
现在我们开始介绍我们提出的光线搜索攻击。我们首先介绍光线搜索攻击的朴素版本，总结在算法 1 中。具体来说，给定一个模型 $f$ 和一个测试样本 {x,y}\{\mathbf{x},y\}{x,y}，我们首先将最佳搜索方向初始化为一个全 1 向量，并将初始最佳半径设置为无穷大。然后我们迭代地改变当前最佳光线方向每个维度的符号，并通过算法 2（稍后描述）测试这个修改后的光线方向是否能产生更好的决策边界半径。如果可以，我们就更新最佳搜索方向和最佳半径；否则，它们保持不变。算法 1 是一个贪婪搜索算法（greedy search algorithm），用于寻找决策边界半径的局部最优值（local optima），其定义如下。

定义 3.1 (决策边界半径的局部最优). 一个光线方向d∈{−1,1}d\mathbf{d}\in\{-1,1\}^{d}d∈{−1,1}d 是关于 (3.4) 的决策边界半径的局部最优，如果对于所有满足$\Vert {\mathbf{d}}^{\prime }-\mathbf{d}{\Vert }_0\le 1$ 的d′∈{−1,1}d\mathbf{d}^{\prime}\in\{-1,1\}^{d}d′∈{−1,1}d，我们有 $g(\mathbf{d})\le g({\mathbf{d}}^{\prime })$。

定理 3.2. 给定足够的查询预算，令 $(\hat{r},\hat{\mathbf{d}})$ 是算法 1 的输出，则 $\hat{\mathbf{d}}$ 是决策边界半径问题 (3.4) 的局部最优解。

证明. 我们通过反证法证明。假设 $\hat{\mathbf{d}}$ 不是局部最优解，那么一定存在某个${\mathbf{d}}^{\prime }$ 满足 $\Vert {\mathbf{d}}^{\prime }-\hat{\mathbf{d}}{\Vert }_0\le 1$（即 ${\mathbf{d}}^{\prime }$ 与 $\hat{\mathbf{d}}$ 最多在一个维度上不同），使得 $g(\hat{\mathbf{d}})>g({\mathbf{d}}^{\prime })$。这意味着算法 1 仍然可以通过遍历所有维度找到比 $g(\hat{\mathbf{d}})$ 更好的解，因此 $\hat{\mathbf{d}}$ 不会是算法 1 的输出。这就导致了矛盾。

接下来我们介绍算法 2，它执行决策边界半径搜索。算法 2 的主体（第 7 行到第 12 行）是一个二分搜索算法（binary search algorithm），用于高精度定位决策边界半径。另一方面，第 7 行之前的步骤侧重于决定搜索范围以及我们是否需要搜索它（这是实现高效攻击的关键）。具体来说，我们首先通过其 $L_2$ 范数对搜索方向进行归一化。然后在第 3 行，我们在点 $\mathbf{x}+{\eta }_{\mathrm{best}}\cdot {\mathbf{d}}_{\eta }{}^2$ 处进行快速检查，并决定是否需要对当前方向进一步执行二分搜索。为了帮助更好地理解底层机制，图 1 提供了算法 2 第 3 行快速检查步骤的二维示意图。假设我们首先在当前最佳方向 ${\mathbf{d}}_{\mathrm{best}}$ 的第 1 维度改变符号，得到修改方向 ${\mathbf{d}}_{tmp1}$。快速检查表明它是一个有效的攻击，并且有潜力进一步减小决策边界半径。另一方面，如果我们改变 ${\mathbf{d}}_{\mathrm{best}}$ 在第 2 维度的符号，得到修改方向 ${\mathbf{d}}_{tmp2}$。快速检查表明它不再是一个有效的攻击，方向 ${\mathbf{d}}_{tmp2}$ 的决策边界半径只能比当前的 ${\eta }_{\mathrm{best}}$ 更差。因此，我们跳过所有旨在估计更差决策边界半径的不必要查询。请注意，在 Cheng 等人 [10] 中，也为轻微扰动的方向提出了类似的检查。然而，他们将其用作梯度估计的符号，而我们根据检查结果简单地丢弃所有不满足条件的半径，从而获得更好的效率。最后，我们解释算法 2 中的第 6 行。
选择$\min (r_{\text{best}},||\mathbf{d}|{|}_2)$ 是因为初始 $r_{\text{best}}$ 是 $\infty$，在快速检查通过的情况下，我们应该确保二分搜索范围是有限的。

3.3 分层搜索

最近关于黑盒攻击的工作[20, 28]发现，梯度的不同维度之间存在一定的空间相关性（spatial correlation），利用这种先验知识可以帮助提高黑盒攻击的效率。因此，他们在原始数据样本上的小块或图像块（tiles or image blocks）上添加相同的扰动以提高效率。受此发现的启发，我们也通过设计光线搜索攻击的分层搜索（hierarchical search）版本来利用这些空间相关性，如算法 3 所示。具体来说，我们添加一个新的阶段变量 $s$。在每个阶段，我们将当前的搜索方向切割成$2^s$ 个小块，并在每次迭代中同时改变整个块的符号作为修改后的光线搜索方向进行决策边界半径搜索。遍历所有块后，我们移动到下一阶段并重复搜索过程。从经验上讲，算法 3 通过利用上述空间相关性极大地提高了搜索效率。我们在第 4 节中的所有实验都是使用算法 3 进行的。注意，如果查询预算足够大，算法 3 最终会达到块大小³等于 $1$ 的情况，并最终退化为算法 1。³ 为了完整性，当 $2^s$ 大于数据维度 $d$ 时，算法 3 将只将搜索方向向量 ${\mathbf{d}}_{\text{tmp}}$ 划分为 $d$ 个块，以确保每个块至少包含一个维度。

注意，所有三个算法（算法 1, 2 和 3）除了最大查询次数（这通常是一个预定义的问题相关参数）外，不涉及任何超参数。与之形成鲜明对比的是，典型的白盒攻击和基于零阶优化的黑盒攻击需要调整相当多的超参数才能获得良好的攻击性能。

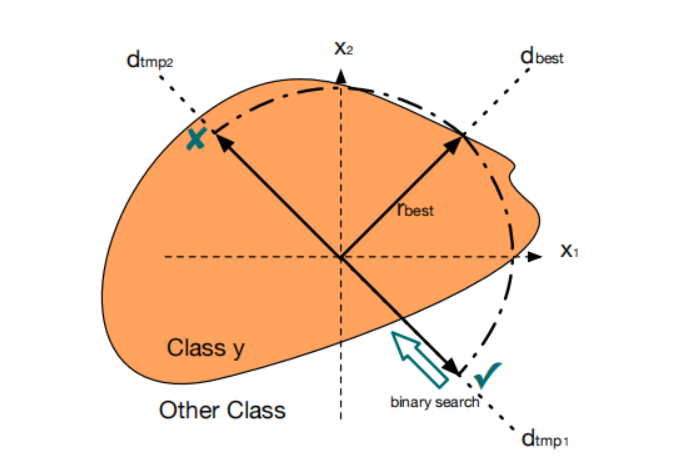
图 1. 算法 2 中快速检查步骤的二维示意图。

4. 实验

在本节中，我们展示了我们提出的光线搜索攻击（RayS）的实验结果。我们首先在自然训练模型（naturally trained models）上使用其他硬标签攻击基线测试 RayS 攻击，然后将 RayS 攻击应用于最近提出的最先进的鲁棒训练模型（robust training models）以测试它们的性能。我们所有的实验都是在 Python 3.6.9 平台上使用 PyTorch 1.3.1 和 NVIDIA 2080 Ti GPU 进行的。

4.1 数据集和目标模型

我们在 MNIST [24]、CIFAR-10 [22] 和 ImageNet [11] 数据集上比较了所有攻击算法的性能。遵循对抗样本文献[1, 19, 28]，我们为 MNIST 数据集设置 $ϵ=0.3$，为 CIFAR-10 数据集设置$ϵ=0.031$，为 ImageNet 数据集设置 $ϵ=0.05$。对于自然训练模型，在 MNIST 数据集上，我们攻击两个预训练的 7 层 CNN：4 个卷积层后接 3 个全连接层，每个卷积层后应用最大池化（Max-pooling）和 ReLU 激活。该 MNIST 预训练模型在测试集上达到 99.5% 的准确率。在 CIFAR-10 数据集上，我们也使用一个 7 层 CNN 结构，包含 4 个卷积层和一个额外的 3 个全连接层，并带有批归一化（Batch-norm）和最大池化层。该 CIFAR-10 预训练模型在测试集上达到 82.5% 的准确率。对于 ImageNet 实验，我们攻击预训练的 ResNet-50 模型 [16] 和 Inception V3 模型 [37]。据报道，预训练的 ResNet-50 模型具有 76.2% 的 top-1 准确率。预训练的 Inception V3 模型据报道具有 78.0% 的 top-1 准确率。对于鲁棒训练模型，我们评估了两个公认的防御方法：对抗训练（Adversarial Training, AdvTraining）[27] 和 TRADES [46]。此外，我们还测试了另外三个最近提出的声称达到最先进鲁棒精度的防御方法：Sensible Adversarial Training (SENSE) [21], Feature Scattering-based Adversarial Training (FeatureScattering) [44], Adversarial Interpolation Training (AdvInterpTraining) [45]。具体来说，对抗训练[27]解决一个 min-max 优化问题以最小化对抗损失。Zhang 等人[46]研究了对抗训练中鲁棒性和准确性的权衡，并提出了一个经验上更鲁棒的模型。Kim 和 Wang [21] 提议在找到有效攻击时停止攻击生成。Zhang 和 Wang [44] 提出了一种无监督的特征散射（feature-scattering）方案用于攻击生成。Zhang 和 Xu [45] 提出了一种对抗插值（adversarial interpolation）方案来生成对抗样本以及对抗标签（adversarial labels），并在这些样本-标签对上进行训练。

4.2 基线方法

我们将提出的算法与几种最先进的攻击算法进行比较。具体来说：

• 对于攻击自然训练模型，我们将提出的 RayS 攻击与其他硬标签攻击基线进行比较：(i) OPT 攻击 [9], (ii) SignOPT 攻击 [10], 和 (iii) HSJA 攻击 [6]。我们采用 OPT、SignOPT 和 HSJA 攻击原始论文中的相同超参数设置。
• 对于攻击鲁棒训练模型，我们额外与其他最先进的黑盒攻击甚至白盒攻击进行比较：(i) PGD 攻击 [27] (白盒), (ii) CW 攻击 [5]⁴ (白盒), (iii) SignHunter [1] (黑盒), 和 (iv) Square 攻击 [2] (黑盒)。对于 PGD 攻击和 CW 攻击，我们将步长设置为 0.007，并提供 20 步和 100 步的攻击结果。对于 SignHunter 和 Square 攻击，我们采用其原始论文中使用的相同超参数设置。

⁴ 准确地说，这里的 CW 攻击指的是使用 CW 损失 [5] 进行 PGD 更新。

4.3 在自然训练模型上与硬标签攻击基线的比较

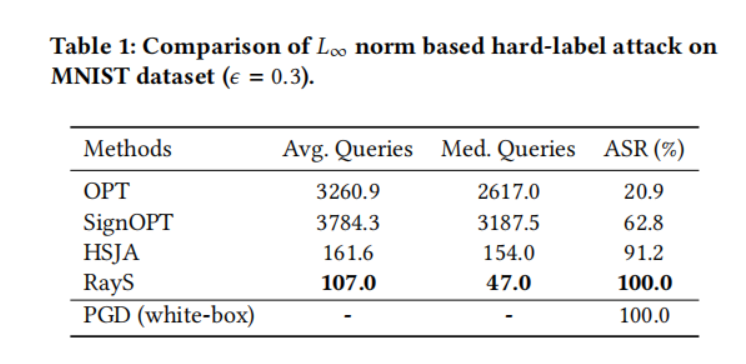
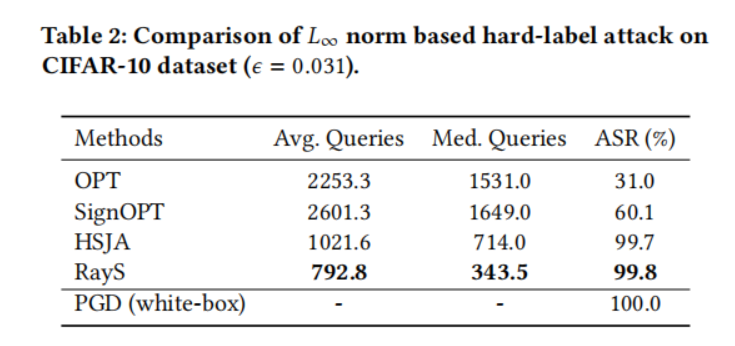
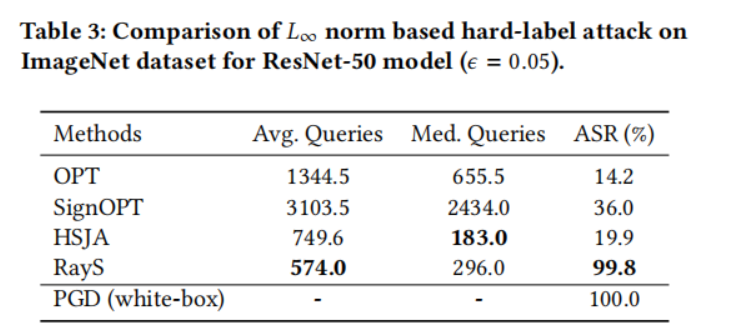
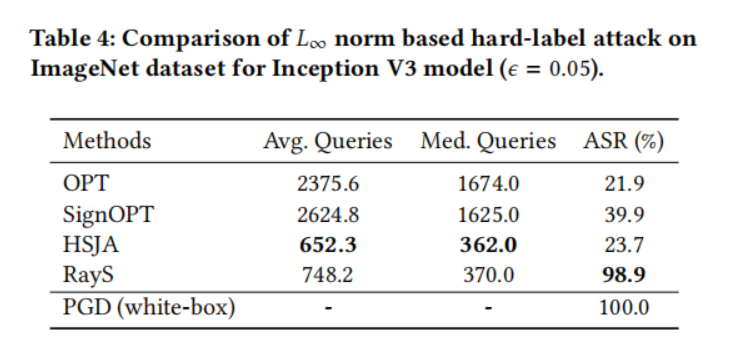
在本小节中，我们在自然训练模型上将我们的光线搜索攻击与其他硬标签攻击基线进行比较。对于每个数据集（MNIST、CIFAR-10 和 ImageNet），我们从其测试集中随机选择 1000 张被预训练模型正确分类的图片，并测试这些图片中有多少张可以被硬标签攻击成功攻击。对于每种方法，我们将最大查询次数限制为 10000。为了提高查询效率，一旦某个测试样本被成功攻击（即对抗样本与原始样本之间的 $L_{\infty }$ 范数距离小于预定义的扰动限制 $ϵ$），我们就停止对该样本的攻击。表 1、2、3 和 4 分别展示了所有硬标签攻击在 MNIST 模型、CIFAR-10 模型、ResNet-50 模型和 Inception V3 模型上的性能比较。对于每个实验，我们报告每种攻击成功所需的平均查询次数（Avg. Queries）和中位数查询次数（Med. Queries），以及最终攻击成功率（ASR, Attack Success Rate），即成功攻击次数占总攻击尝试次数的比例。具体来说：

• 在 MNIST 数据集上，我们观察到我们提出的 RayS 攻击在平均查询次数和中位数查询次数方面具有更好的查询效率，并且比 OPT 和 SignOPT 方法具有更高的攻击成功率。注意 SignOPT 的平均（中位数）查询次数大于 OPT。然而，这并不意味着 SignOPT 比 OPT 表现更差。这个结果是由于 OPT 的攻击成功率非常低，其平均（中位数）查询次数是基于成功攻击的样本计算的，在这种情况下，这些样本是最脆弱的样本。HSJA 攻击虽然比 SignOPT⁵ 有所改进，但仍然落后于我们的 RayS 攻击。
• 对于 CIFAR-10 模型，RayS 攻击仍然达到了最高的攻击成功率。尽管 HSJA 攻击在攻击成功率方面接近 RayS 攻击，但其查询效率仍然落后。
• 在 ResNet-50 和 Inception V3 模型上，只有 RayS 攻击保持了较高的攻击成功率，而其他基线则大幅落后。注意 HSJA 攻击在 ImageNet 模型上实现了相似甚至略好的平均（中位数）查询次数，这表明 HSJA 对于最脆弱的样本是高效的，但在处理难以攻击的样本时效果不佳。

图 2 显示了在不同模型上，所有基线方法的攻击成功率随查询次数变化的曲线图。我们再次可以看到，与其他硬标签攻击基线相比，RayS 攻击总体上实现了最高的攻击成功率和最好的查询效率。

⁵ 原文此处为“SignOPT”，但根据上下文（CIFAR-10表2中HSJA成功率99.7% > SignOPT的60.1%），应为“OPT”。此处按原文翻译。

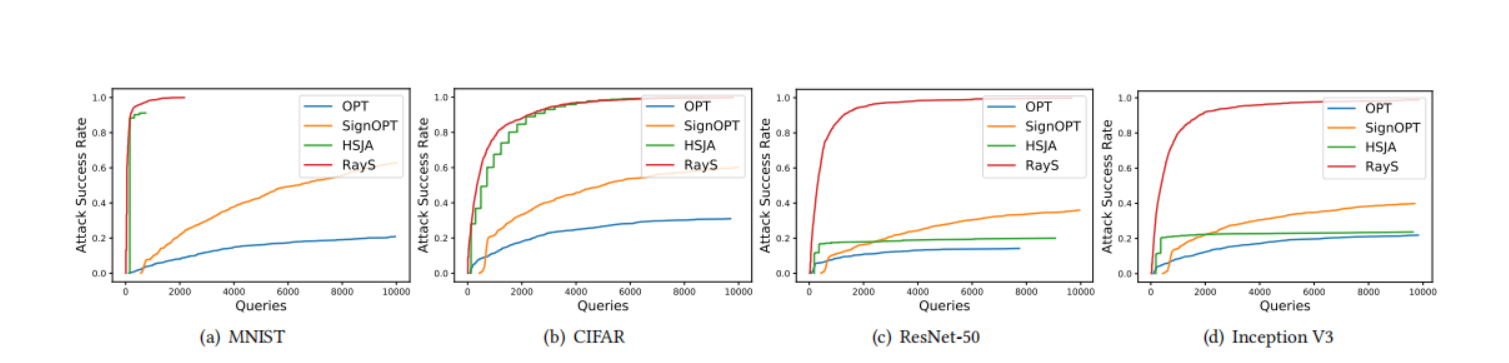
图 2. MNIST、CIFAR-10 和 ImageNet 数据集上不同硬标签攻击的攻击成功率随查询次数变化图。

4.4 评估最先进鲁棒模型的鲁棒性

在本小节中，我们通过将我们提出的光线搜索攻击应用于最先进的鲁棒训练模型来进一步测试它。具体来说，我们在 CIFAR-10 数据集和 WideResNet（Wu 等人, 2019）架构上选择了五个最近提出的开源防御模型。对于测试样本，我们从 CIFAR-10 测试集中随机选择 1000 张图像。我们将最大查询次数设置为 40000。

在评估指标方面，遵循鲁棒训练文献（Zhang 等人, 2017; Wang 等人, 2018），我们报告防御模型的自然精度（natural accuracy）和鲁棒精度（robust accuracy，即在对抗攻击下的分类精度）。此外，我们报告了一个名为**平均决策边界距离（Average Decision Boundary Distance, ADBD）**的新指标，它定义为所有测试样本到其最近决策边界的平均 $L_{\infty }$ 范数距离。注意，ADBD 对于遵循公式 (3.1) 的白盒和黑盒攻击无效，因为它们无法为所有测试样本找到最近的决策边界。

这里我们想强调 ADBD 与对抗学习文献中的平均 $L_{\infty }$ 失真（$L_{\infty }$ distortion）的区别。注意，$L_{\infty }$ 失真⁶ 通常指的是成功的对抗攻击样本与其对应的原始干净样本之间的 $L_{\infty }$ 范数距离，因此，它受到最大扰动限制 $ϵ$ 选择的影响。对于硬标签攻击，只考虑半径小于 $ϵ$ 的攻击会丢失太多信息，无法捕捉模型鲁棒性的全貌⁷。另一方面，ADBD 指标虽然仅对硬标签攻击有效，但它提供了对原始干净样本到其决策边界的平均距离的有意义估计。

⁶ 在本实验中测试的所有白盒和黑盒攻击，它们的$L_{\infty }$ 失真都非常接近扰动限制$ϵ=0.031$。因此，我们在表格中没有报告 $L_{\infty }$ 失真，因为它没有提供太多额外信息。
⁷ 对于硬标签攻击，ADBD 值总是大于 $L_{\infty }$ 失真。

表 5、6、7、8 和 9 显示了在五个选定的鲁棒模型上不同对抗攻击方法的比较结果。具体来说：

• 对于两个公认的鲁棒训练模型，对抗训练（表 5）和 TRADES（表 6），我们观察到白盒攻击仍然是最强的攻击，其中 PGD 攻击和 CW 攻击实现了非常相似的攻击性能。对于黑盒攻击，

SignHunter 攻击和 Square 攻击实现了与其白盒对应物相似的攻击性能。在硬标签攻击方面，我们提出的 RayS 攻击在对目标模型访问权限最严格的情况下，也实现了与黑盒甚至白盒攻击相当的攻击性能。当与其他硬标签攻击基线比较时，可以看出我们的 RayS 攻击在鲁棒精度（超过 20%）和平均决策边界距离（减少 30%）方面都取得了显著的性能提升。攻击 $L_{\infty }$ 范数威胁模型的效果较差使得 SignOPT 攻击和 HSJA 攻击不太实用。

• 对于 Sensible Adversarial Training 模型（表 7），与对抗训练和 TRADES 相比，它在白盒攻击下确实实现了总体上更好的鲁棒精度。对于黑盒攻击，SignHunter 攻击实现了与 PGD 攻击相似的性能，Square 攻击实现了与 CW 攻击相似的性能。有趣的是，我们观察到对于硬标签攻击，我们提出的 RayS 攻击实现了 42.5% 的鲁棒精度，比 PGD 攻击降低了 20%，比 CW 攻击降低了 15%，这表明 Sensible Adversarial Training 的鲁棒性实际上并不比 TRADES 和对抗训练更好，只是在 PGD 攻击和 CW 攻击下看起来更好。
• 对于基于特征散射的对抗训练模型（Feature Scattering-based Adversarial Training，表 8），注意 CW 攻击比 PGD 攻击有效得多。同样对于黑盒攻击，Square 攻击的性能比 SignHunter 攻击好得多⁶，这表明在攻击基于特征散射的对抗训练模型时，CW 损失比交叉熵损失更有效。再次，我们可以观察到我们提出的 RayS 攻击将 PGD 攻击的鲁棒精度降低了 28%，将 CW 攻击的鲁棒精度降低了 10%。这也表明基于特征散射的对抗训练模型并没有真正提供比对抗训练或 TRADES 更好的鲁棒性。
• 对于对抗插值训练模型（Adversarial Interpolation Training，表 9），在白盒攻击下，它实现了惊人的高鲁棒精度 75.3%（在 PGD 攻击下）和 68.9%（在 CW 攻击下），在相应的黑盒攻击下也能获得类似的结果。然而，在我们的 RayS 攻击下，它仍然不是真正鲁棒的，将 PGD 攻击的鲁棒精度降低了 28%，CW 攻击降低了 22%。注意，在这个实验中，HSJA 攻击也实现了比 PGD 攻击更低的鲁棒精度，这表明所有硬标签攻击都可能具有检测那些欺骗当前白盒/黑盒攻击的虚假鲁棒模型的潜力，但 HSJA 的低效率限制了其更广泛使用的能力。

⁶ Square 攻击基于 CW 损失，而 SignHunter 攻击基于交叉熵损失。

为了获得五个选定的鲁棒训练模型在我们提出的 RayS 攻击下鲁棒性的总体比较，我们在图 3 中绘制了平均决策边界距离（ADBD）随 RayS 攻击迭代次数的变化图，在图 4 中绘制了鲁棒精度随 RayS 攻击迭代次数的变化图。首先，可以看出平均决策边界距离和鲁棒精度确实在大约 10000 次 RayS 攻击迭代后收敛并保持稳定。图 3 和图 4 表明，在五个选定的鲁棒训练模型中，TRADES 和对抗训练仍然是最鲁棒的模型，而 Sensible Adversarial Training、Feature Scattering-based Adversarial Training 和 Adversarial Interpolation Training 在 PGD 攻击和 CW 攻击下表现出的鲁棒性并不像它们看起来那样好。还要注意，尽管 Sensible Adversarial Training、Feature Scattering-based Adversarial Training 和 Adversarial Interpolation Training 在 RayS 攻击下的鲁棒精度结果差异很大，但它们的 ADBD 结果非常相似。

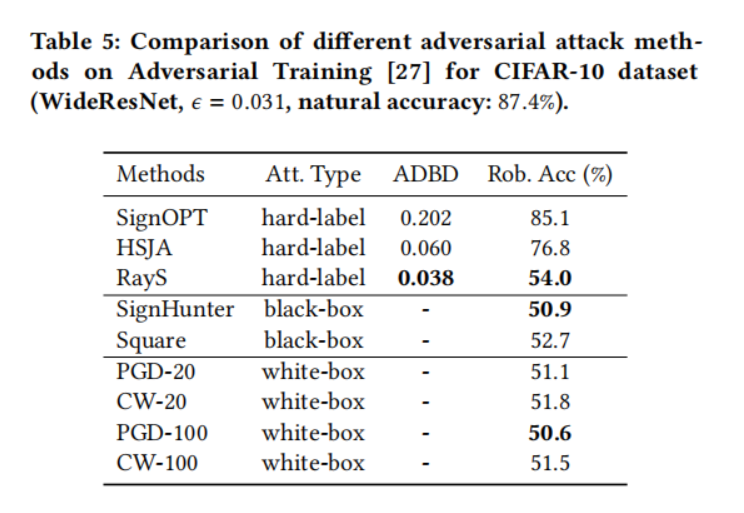
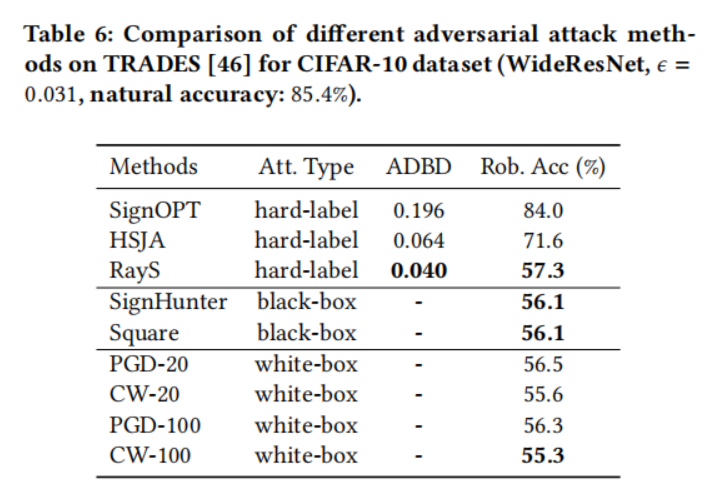
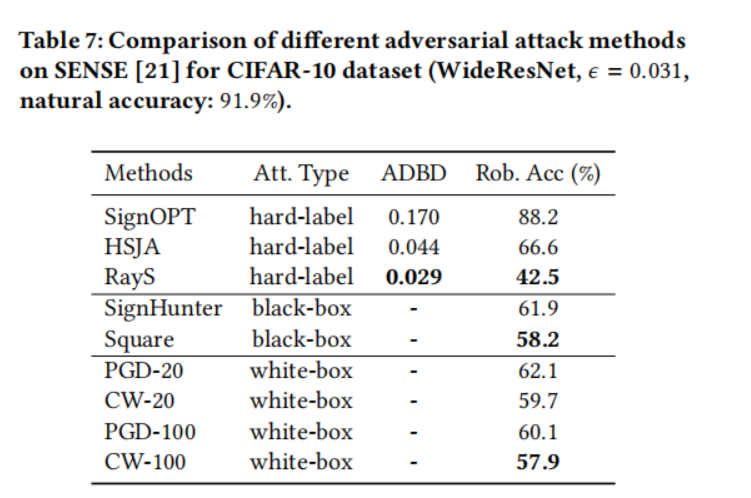
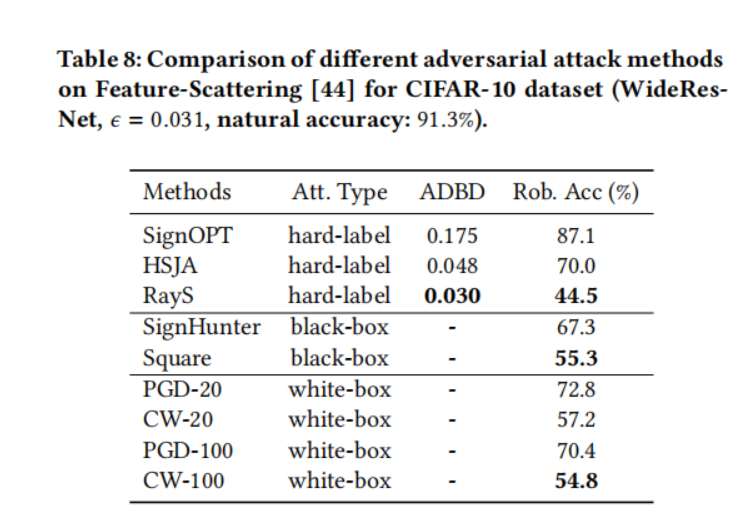
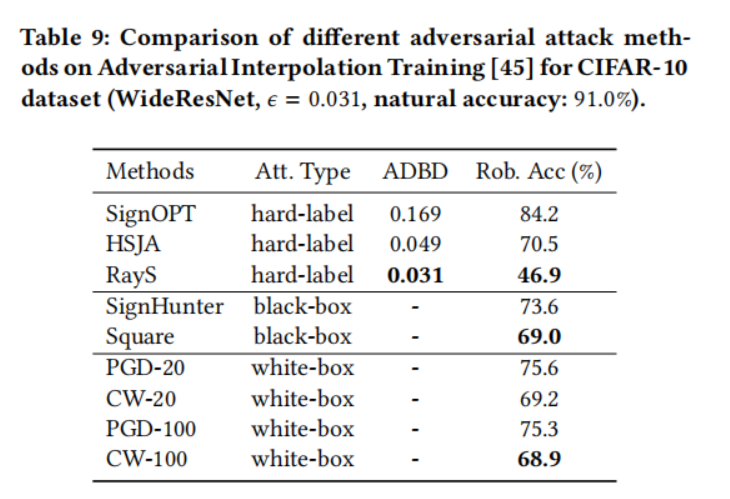
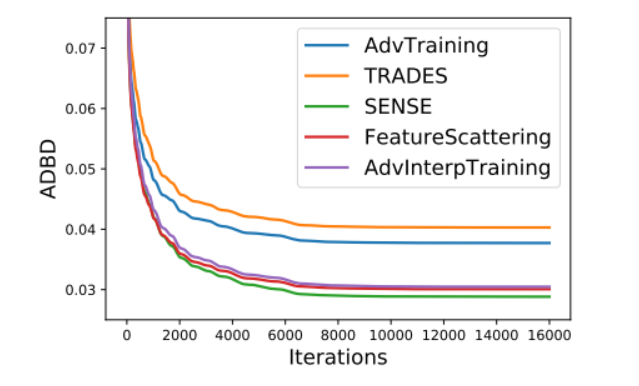
图 3. 几个鲁棒模型的平均决策边界距离（ADBD）随 RayS 攻击迭代次数变化图。

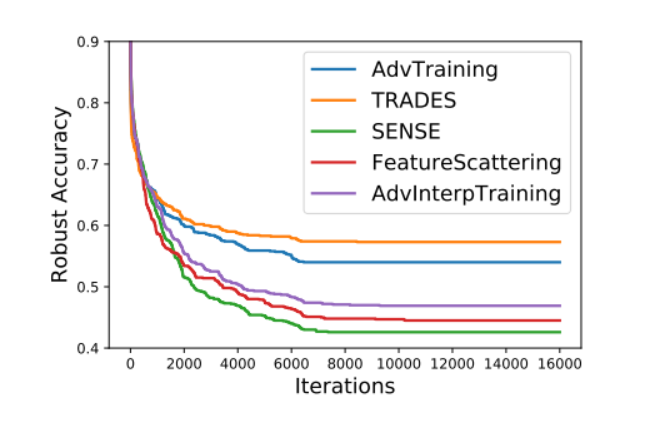
图 4. 几个鲁棒模型的鲁棒精度随 RayS 攻击迭代次数变化图。

5. 讨论与结论

在本文中，我们提出了光线搜索攻击（Ray Searching attack），它只需要目标模型的硬标签输出。所提出的光线搜索攻击在攻击成功率方面比其他硬标签攻击更有效，在查询复杂度方面也更高效。此外，它可以用作检测可能欺骗当前白盒和黑盒攻击的“虚假鲁棒”模型的健全性检查工具。

在下面的讨论中，我们尝试分析所提出的光线搜索攻击成功的关键要素。

• 为什么 RayS 攻击比其他硬标签基线更有效和高效？
  正如我们之前提到的，传统的硬标签攻击更侧重于 $L_{2} $ 范数威胁模型，只有少数扩展到 $L_{\infty }$ 范数威胁模型。而对于我们的 RayS 攻击，我们基于 $L_{\infty }$ 范数威胁模型中的经验发现，将寻找最近决策边界的连续问题重新表述为一个离散问题，从而产生了一种更有效的硬标签攻击。另一方面，直接搜索最近决策边界的策略加上快速检查步骤，消除了不必要的搜索，显著提高了攻击效率。

• 为什么 RayS 攻击可以检测到可能的“虚假”鲁棒模型，而传统的白盒和黑盒攻击不能？
  我们从第 4 节观察到的一件事是，尽管不同的攻击导致不同的鲁棒精度结果，但它们的攻击性能与攻击损失函数的选择相关。例如，PGD 攻击和 SignHunter 攻击都利用交叉熵损失，在大多数情况下它们的攻击性能相似。对于 CW 攻击和 Square 攻击（两者都利用 CW 损失函数）也可以看到类似的效果。然而，这些损失函数被用作问题 (3.1) 的替代损失，它们可能无法真正反映中间样本（一个靠近原始干净样本但还不是有效对抗样本的样本）的质量/潜力。例如，考虑这种情况：两个中间样本在真实类别 $y$ 上具有相同的对数概率，但在其他类别上差异很大。在这种情况下，它们的交叉熵损失是相同的，但其中一个可能比另一个有更大的潜力发展成一个有效的对抗样本（例如，第二大概率接近最大概率）。因此，交叉熵损失并不能真正反映中间样本的真实质量/潜力。类似的情况也可以为 CW 损失构造。与之形成鲜明对比的是，我们的 RayS 攻击将决策边界半径视为搜索准则²。当我们比较决策边界上的两个样本时，显然更近的那个更好。在攻击问题难以解决且攻击者容易陷入中间样本的情况下（例如，攻击鲁棒训练模型），很容易看出 RayS 攻击有更好的机会找到成功的攻击。这部分解释了 RayS 攻击在检测“虚假鲁棒”模型方面的优越性。

我们提出的光线搜索攻击是硬标签对抗攻击领域的一个有前景的方向。它提供了一种高效、有效且易于使用的方法来评估模型在最严格的威胁模型下的鲁棒性，并有助于揭示潜在的虚假鲁棒性。

致谢

我们感谢匿名审稿人和高级程序委员会的宝贵意见。本研究部分由国家科学基金会 CIF-1911168、SaTC-1717950 和 CAREER Award 1906169 赞助。本文中包含的观点和结论是作者的观点和结论，不应被解释为代表任何资助机构的观点。

参考文献

[1] Abdullah Al-Dujaili and Una-May O’Reilly. 2020. Sign Bits Are All You Need for
Black-Box Attacks. In International Conference on Learning Representations.
[2] Maksym Andriushchenko, Francesco Croce, Nicolas Flammarion, and Matthias
Hein. 2019. Square Attack: a query-efficient black-box adversarial attack via
random search. arXiv preprint arXiv:1912.00049 (2019).
[3] Anish Athalye, Nicholas Carlini, and David Wagner. 2018. Obfuscated Gradients
Give a False Sense of Security: Circumventing Defenses to Adversarial Examples.
In International Conference on Machine Learning.
[4] Wieland Brendel, Jonas Rauber, and Matthias Bethge. 2018. Decision-Based Adversarial Attacks: Reliable Attacks Against Black-Box Machine Learning Models.
In International Conference on Learning Representations.
[5] Nicholas Carlini and David Wagner. 2017. Towards evaluating the robustness
of neural networks. In 2017 IEEE Symposium on Security and Privacy (SP). IEEE,
39–57.
[6] Jianbo Chen, Michael I Jordan, and Martin J Wainwright. 2019. Hopskipjumpattack: A query-efficient decision-based attack. arXiv preprint arXiv:1904.02144 3
(2019).
[7] Jinghui Chen, Dongruo Zhou, Jinfeng Yi, and Quanquan Gu. 2020. A Frank-Wolfe
framework for efficient and effective adversarial attacks. AAAI (2020).
[8] Pin-Yu Chen, Huan Zhang, Yash Sharma, Jinfeng Yi, and Cho-Jui Hsieh. 2017.
Zoo: Zeroth order optimization based black-box attacks to deep neural networks
without training substitute models. In Proceedings of the 10th ACM Workshop on
Artificial Intelligence and Security. ACM, 15–26.
[9] Minhao Cheng, Thong Le, Pin-Yu Chen, Huan Zhang, JinFeng Yi, and Cho-Jui
Hsieh. 2019. Query-Efficient Hard-label Black-box Attack: An Optimization-based
Approach. In International Conference on Learning Representations.
[10] Minhao Cheng, Simranjit Singh, Patrick H. Chen, Pin-Yu Chen, Sijia Liu, and
Cho-Jui Hsieh. 2020. Sign-OPT: A Query-Efficient Hard-label Adversarial Attack.
In International Conference on Learning Representations.
[11] Jia Deng, Wei Dong, Richard Socher, Li-Jia Li, Kai Li, and Li Fei-Fei. 2009. Imagenet: A large-scale hierarchical image database. In Computer Vision and Pattern
Recognition, 2009. CVPR 2009. IEEE Conference on. Ieee, 248–255.
[12] Guneet S Dhillon, Kamyar Azizzadenesheli, Zachary C Lipton, Jeremy Bernstein,
Jean Kossaifi, Aran Khanna, and Anima Anandkumar. 2018. Stochastic activation
pruning for robust adversarial defense. International Conference on Learning
Representations (2018).
[13] Ian J Goodfellow, Jonathon Shlens, and Christian Szegedy. 2015. Explaining and
harnessing adversarial examples. International Conference on Learning Representations (2015).
[14] Chuan Guo, Mayank Rana, Moustapha Cisse, and Laurens Van Der Maaten.
2018. Countering adversarial images using input transformations. International
Conference on Learning Representations (2018).
[15] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2016. Deep residual
learning for image recognition. In CVPR. 770–778.
[16] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2016. Identity mappings
in deep residual networks. In European Conference on Computer Vision. Springer,
630–645.
[17] Geoffrey Hinton, Li Deng, Dong Yu, George Dahl, Abdel-rahman Mohamed,
Navdeep Jaitly, Andrew Senior, Vincent Vanhoucke, Patrick Nguyen, Brian Kingsbury, et al. 2012. Deep neural networks for acoustic modeling in speech recognition. IEEE Signal processing magazine 29 (2012).
[18] Weiwei Hu and Ying Tan. 2017. Generating adversarial malware examples for
black-box attacks based on GAN. arXiv preprint arXiv:1702.05983 (2017).
[19] Andrew Ilyas, Logan Engstrom, Anish Athalye, Jessy Lin, Anish Athalye, Logan
Engstrom, Andrew Ilyas, and Kevin Kwok. 2018. Black-box Adversarial Attacks
with Limited Queries and Information. In Proceedings of the 35th International
Conference on Machine Learning.
[20] Andrew Ilyas, Logan Engstrom, and Aleksander Madry. 2019. Prior convictions:
Black-box adversarial attacks with bandits and priors. International Conference
on Learning Representations (2019).
[21] Jungeum Kim and Xiao Wang. 2020. Sensible adversarial learning. https:
//openreview.net/forum?id=rJlf_RVKwr
[22] Alex Krizhevsky, Geoffrey Hinton, et al. 2009. Learning multiple layers of features
from tiny images. (2009).
[23] Alexey Kurakin, Ian Goodfellow, and Samy Bengio. 2016. Adversarial examples
in the physical world. arXiv preprint arXiv:1607.02533 (2016).
[24] Yann LeCun, Corinna Cortes, and CJ Burges. 2010. MNIST handwritten digit
database. (2010).
[25] Yandong Li, Lijun Li, Liqiang Wang, Tong Zhang, and Boqing Gong. 2019. NATTACK: Learning the Distributions of Adversarial Examples for an Improved
Black-Box Attack on Deep Neural Networks. In International Conference on Machine Learning. 3866–3876.
[26] Xingjun Ma, Bo Li, Yisen Wang, Sarah M Erfani, Sudanthi Wijewickrema, Grant
Schoenebeck, Dawn Song, Michael E Houle, and James Bailey. 2018. Characterizing adversarial subspaces using local intrinsic dimensionality. International
Conference on Learning Representations (2018).
[27] Aleksander Madry, Aleksandar Makelov, Ludwig Schmidt, Dimitris Tsipras, and
Adrian Vladu. 2018. Towards deep learning models resistant to adversarial attacks.
International Conference on Learning Representations (2018).
[28] Seungyong Moon, Gaon An, and Hyun Oh Song. 2019. Parsimonious Black-Box
Adversarial Attacks via Efficient Combinatorial Optimization. In International
Conference on Machine Learning. 4636–4645.
[29] Seyed-Mohsen Moosavi-Dezfooli, Alhussein Fawzi, and Pascal Frossard. 2016.
Deepfool: a simple and accurate method to fool deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2574–
2582.
[30] Nicolas Papernot, Patrick McDaniel, and Ian Goodfellow. 2016. Transferability
in machine learning: from phenomena to black-box attacks using adversarial
samples. arXiv preprint arXiv:1605.07277 (2016).
[31] Nicolas Papernot, Patrick McDaniel, Ian Goodfellow, Somesh Jha, Z Berkay
Celik, and Ananthram Swami. 2017. Practical black-box attacks against machine
learning. In Proceedings of the 2017 ACM on Asia Conference on Computer and
Communications Security. ACM, 506–519.
[32] Nicolas Papernot, Patrick McDaniel, Somesh Jha, Matt Fredrikson, Z Berkay Celik,
and Ananthram Swami. 2016. The limitations of deep learning in adversarial
settings. In Security and Privacy (EuroS&P), 2016 IEEE European Symposium on.
IEEE, 372–387.
[33] Nicolas Papernot, Patrick McDaniel, Xi Wu, Somesh Jha, and Ananthram Swami.
2016. Distillation as a defense to adversarial perturbations against deep neural
networks. In 2016 IEEE Symposium on Security and Privacy (SP). IEEE, 582–597.
[34] Pouya Samangouei, Maya Kabkab, and Rama Chellappa. 2018. Defense-gan:
Protecting classifiers against adversarial attacks using generative models. International Conference on Learning Representations (2018).
[35] Yang Song, Taesup Kim, Sebastian Nowozin, Stefano Ermon, and Nate Kushman.
2018. Pixeldefend: Leveraging generative models to understand and defend
against adversarial examples. International Conference on Learning Representations
(2018).
[36] Ilya Sutskever, Geoffrey E Hinton, and A Krizhevsky. 2012. Imagenet classification with deep convolutional neural networks. Advances in neural information
processing systems (2012), 1097–1105.
[37] Christian Szegedy, Vincent Vanhoucke, Sergey Ioffe, Jon Shlens, and Zbigniew
Wojna. 2016. Rethinking the inception architecture for computer vision. In
Proceedings of the IEEE conference on computer vision and pattern recognition.
2818–2826.
[38] Christian Szegedy, Wojciech Zaremba, Ilya Sutskever, Joan Bruna, Dumitru Erhan,
Ian Goodfellow, and Rob Fergus. 2013. Intriguing properties of neural networks.
arXiv preprint arXiv:1312.6199 (2013).
[39] Jonathan Uesato, Brendan OâĂŹDonoghue, Pushmeet Kohli, and Aaron Oord.
2018. Adversarial Risk and the Dangers of Evaluating Against Weak Attacks. In
International Conference on Machine Learning. 5025–5034.
[40] Yisen Wang, Xingjun Ma, James Bailey, Jinfeng Yi, Bowen Zhou, and Quanquan
Gu. 2019. On the Convergence and Robustness of Adversarial Training. In
International Conference on Machine Learning. 6586–6595.
[41] Yisen Wang, Difan Zou, Jinfeng Yi, James Bailey, Xingjun Ma, and Quanquan
Gu. 2020. Improving Adversarial Robustness Requires Revisiting Misclassified
Examples. In International Conference on Learning Representations.
[42] Cihang Xie, Jianyu Wang, Zhishuai Zhang, Zhou Ren, and Alan Yuille. 2018.
Mitigating adversarial effects through randomization. International Conference
on Learning Representations (2018).
[43] Sergey Zagoruyko and Nikos Komodakis. 2016. Wide residual networks. arXiv
preprint arXiv:1605.07146 (2016).
[44] Haichao Zhang and Jianyu Wang. 2019. Defense against adversarial attacks using
feature scattering-based adversarial training. In Advances in Neural Information
Processing Systems. 1829–1839.
[45] Haichao Zhang and Wei Xu. 2020. Adversarial Interpolation Training: A Simple
Approach for Improving Model Robustness. https://openreview.net/forum?id=
Syejj0NYvr
[46] Hongyang Zhang, Yaodong Yu, Jiantao Jiao, Eric Xing, Laurent El Ghaoui, and
Michael Jordan. 2019. Theoretically Principled Trade-off between Robustness
and Accuracy. In International Conference on Machine Learning. 7472–7482.