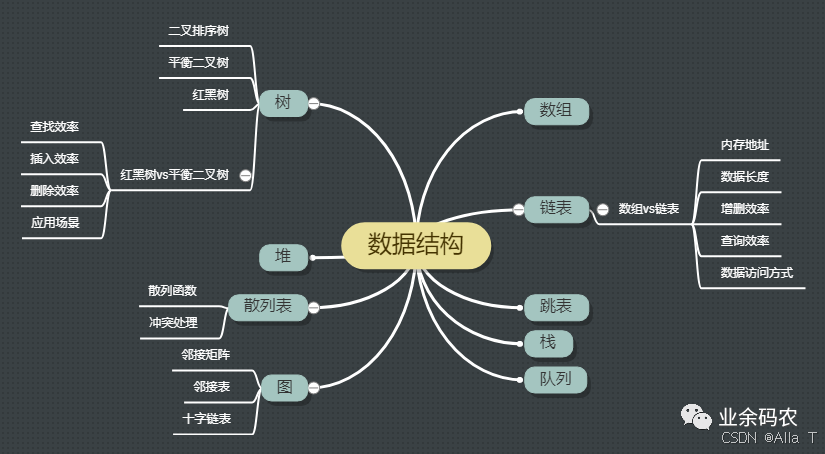
数据结构=逻辑结构+物理结构(存储结构),数据结构是计算机中存储、组织数据的方式。
其中物理结构是数据的逻辑结构在计算机中的存储形式。而存储器针对内存而言,像硬盘、软盘、光盘等外部存储器的数据组织常用文件结构描述。
1. 基础算法
1.1 递归Recursion
- 函数在定义中使用函数自身的方法,例子是求斐波那契数列。
long long Fib(int i) {if(i<=1) return i;return Fib(i-1)+Fib(i-2); }
1.2 分治Divide and Conquer
分治,即分而治之。☞将大问题分成几个小部分计算,最后再将小部分结果合并起来
- 要考虑什么时候是基础情况,很多时候依靠递归实现
int RecSum(int l, int r) {int mid = l + r >> 1; // 因为这里是位运算,相当于整数除以2;该写法常见于二分查找、分治算法等腰计算中间值return RecSum(l,mid)+RecSum(mid+l, r);
}
这段代码是递归求和函数,但因为没有终止条件会导致无限递归和栈溢出(stack overflow)。即没有处理l==r的情况,修正后
int RecSum(int l, int r) {if (l==r) return l;int mid =
}
1.3 贪心算法
- 基本思想
1)求解最优化问题的算法包含一系列步骤
2)每一步都有一组选择
3)做出当前最好的选择
4)通过局部最优选择达到全局最优-> 未必达到全局最优
5)是否能达到最优解需严格证明 - 产生最优解的条件
1)最优子结构:
2)贪心选择性:
2. 线性表
数据的存储结构应正确反映数据元素间的逻辑关系
体现为线性表的顺序存储能用数据实现,而元素物理
1)个数有限;2)元素有先后次序;3)数据类型相同;4)讨论元素间的逻辑关系
一旦数据被线性表存储,在逻辑上的相对位置就固定下来了。线性表分为顺序表和链表。其中链式存储允许存储空间不连续,但顺序表不行。
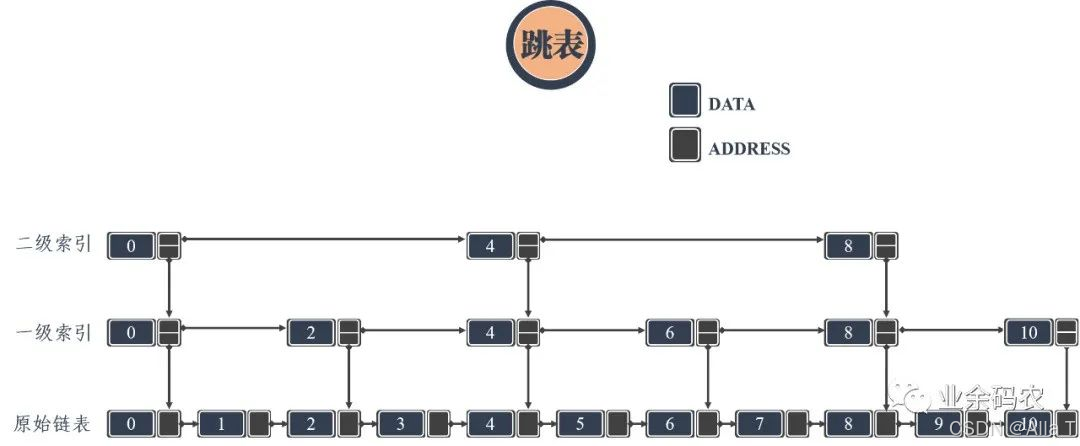
2.1 跳表
上面的对比中可以看出,链表虽然通过增加指针域提升了自由度,但是却导致数据的查询效率恶化。特别是当链表长度很长的时候,对数据的查询还得从头依次查询,这样的效率会更低。跳表的产生就是为了解决链表过长的问题,通过增加链表的多级索引来加快原始链表的查询效率。这样的方式可以让查询的时间复杂度从O(n)提升至O(logn)。
1)
2)
3)
3. 栈
3.1 栈
遵守LIFO原则(后进先出)
3.2 队列
遵守FIFO原则(先进先出)
4. 树
4.1 二叉树(Binary Tree)
- 特点:除了最后一层外,其他层节点必须完全填满(每层从左到右没有空缺),最后一层的节点必须连续集中在左侧(允许右侧有空缺但左侧不能有)
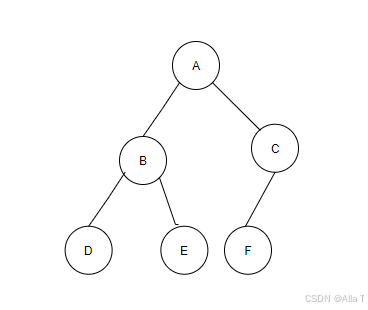
- 二叉树代码
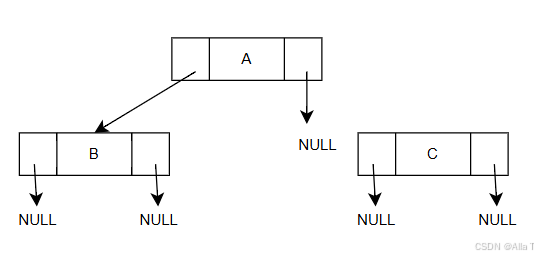
此处是链式存储typedef struct BiNode {char data;struct BiTNode *lchild, *rchild; // 左右孩子指针 } BiTNode, *BiTree; BiTree root = NULL; // 根节点 root = (BiTree)malloc(sizeof(BiTNode)); root -> data = 'A'; root -> lchild = NULL; root -> rchild = NULL; // 插入结点B BiTNode *BNode = NULL; BNode = (BiTNode*)malloc(sizeof(BiTNode)); BNode->data = 'B'; BNode->lchild = NULL; BNode->rchild = NULL; root->lchild = BNode; // 定义了B之后才将A对应的root的左子树连接到B中 // 插入结点C BiTNode *CNode = NULL; CNode = (BiTNode*)malloc(sizeof(BiTNode)); CNode -> data = 'C'; CNode -> lchild = NULL; CNode -> rchild = NULL; root -> rchild = CNode; - 二叉树
4.2 B+树
MySQL InnoDB索引(B+树)作为主要的索引结构,用于主键索引(聚簇索引)和辅助索引(二级索引)。B+树相比于AVL树、红黑树等数据结构,更适合数据库的大规模数据存储和磁盘存取优化。
-
B+:平衡树(非二叉树),具有以下特点
1)每个B+树的结点中含有n个关键字,而B+树每个节点中关键字个数n的取值范围是⌈m/2⌉≤n≤m⌈m/2⌉≤n≤m⌈m/2⌉≤n≤m
2)所有的叶子节点包含了关键字的信息,及指向关键字记录的指针,且叶子节点本身依关键字的大小自小而大顺序链接。
3)所有非终端节点(非叶子)是索引,结点中仅含有其子树(根节点)中最大/小的关键字 -
1
-
1
4.3 AVL树
4.4
5. 图
5.1 图的
6. 哈希表
- 概念:哈希表指通过哈希函数将键值映射到值的数据结构
- 哈希冲突:通过哈希查找发现该位置上已有对应的关键码值,发生冲突
- 解决冲突的方法:
1)开发地址法:寻找另一个空闲地址,包括线性探测法和平方探测法
2)链地址法:将所有哈希地址相同的记录链接到同一链表中,适用于频繁插入删除
3)再哈希法:使用其他哈希函数计算新的地址 - 相关的代码
// 两数之和:给定一个整数数组nums和整数目标值target,请在该数组中找出和为目标值target的两个整数,并返回数组下标
class Solution {
public: vector<int> twoSum(vector<int>& nums, int target) {vector<int> ret;}
}6.1
7. 堆
用于动态内存管理
7.1
8. 动态规划
将会定义两个关键:一是动态规划,二是状态转移。
其中状态定义是把求解过程中所有状态(子问题)表示出来是动态规划的难点
8.1 区间dp和树形dp
8.2
8.3 常见问题
- 朴素区间dp:在区间上进行dp,主要思路是通过合并小区间得到大区间的最优解
大区间是cost[i][j][k],其中包含dp[i][j]和dp[j][k],将其合并为区间dp[i][k] = dp[i][j] + dp[j][k] + cost[i][j][k]
动态规划将会定义两个关键,一是状态定义二是状态装
- 破坏成链
- 经典树形dp
- 树形背包
- 树形背包优化
9. 排序
9.1 快速排序(三路版)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// 三路快速排序(递归版本)
void quickSort3Way(vector<int>& nums, int left, int right) {if (left>=right) return; // 递归终止条件// 选择基准值(选择中间元素)int pivot = nums[left+(right-left)/2];// 初始化三个指针}
10. 并查集
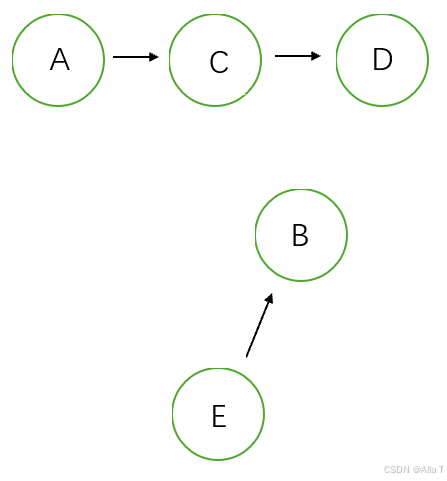
- 基础概念:并查集是一种树型数据结构用于处理不相交集合(disjoint sets)的合并及查询问题,常在使用中部用森林表示。
A−BA-BA−B - 合并方式:




—享元模式)
)






)



)


