加法器
框架，首先介绍原理，然后引入一位加法器最后再引入多位加法器最后引入带符号的加法器
这一节涉及到的硬件电路的知识理解就好，实在看不懂就跳过，但是封装以后的功能必须看懂。
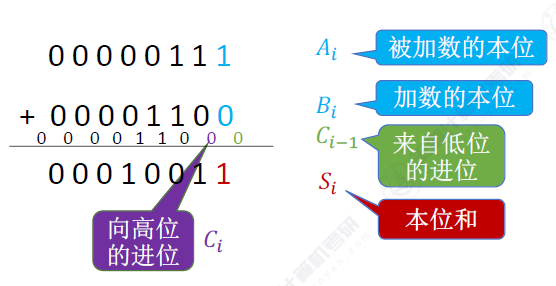
这是一个一般的加法过程涉及到的必要元素图中已经给出，加数与被加数的本位以及相加以后的本为和，低位的进位和高位的进位
主要就是上面这五部分，首先对于加数与被加数的本位以及低位的进位是输入的内容我们不需要管
接下来我们看本为和，因为二进制加法满二进一的特性使得我们可以采用异或来算本位和。
。可以采用 下面的电路来实现
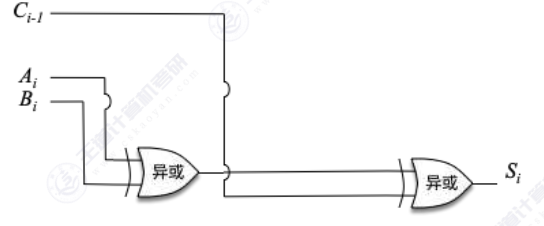
对于向高位的进位来说需要考虑的元素就比较多了。需要考虑加数被加数低位的进位这三个因素，同时结合二进制数的加法规则来看。
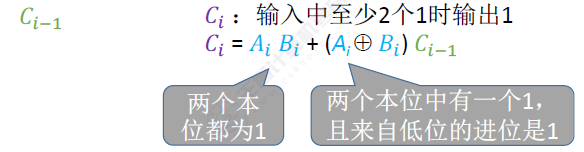
高位的进位有以下图片的情形，图片中采用了或运算来求值，或运算的法则全0为0
第一部分采用与运算当两个都为1时才为1
第二部分先用AB异或（同0异1）再与地位进位相与
满足任意一部分进位为1
电路表示如下图
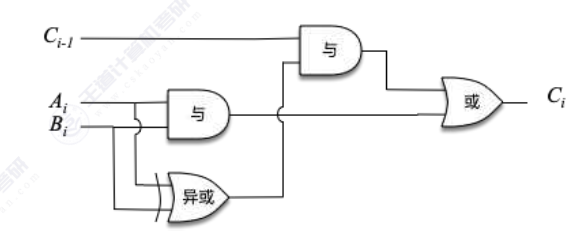
最后结合一下电路图
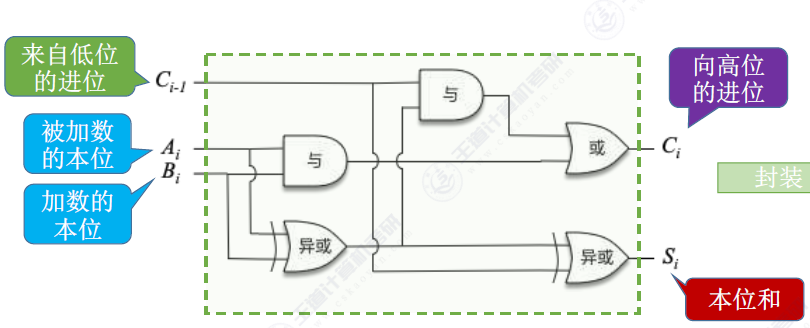
再封装一下
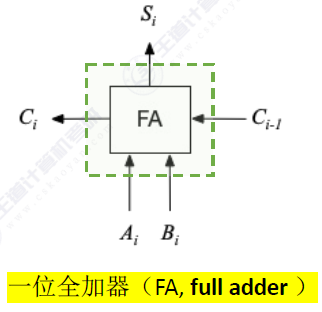
需要记住一下逻辑表达式
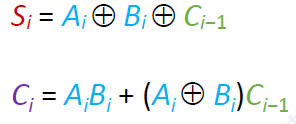
把n 个一位全加器串接起来，就可进行两个n bit数的相加。
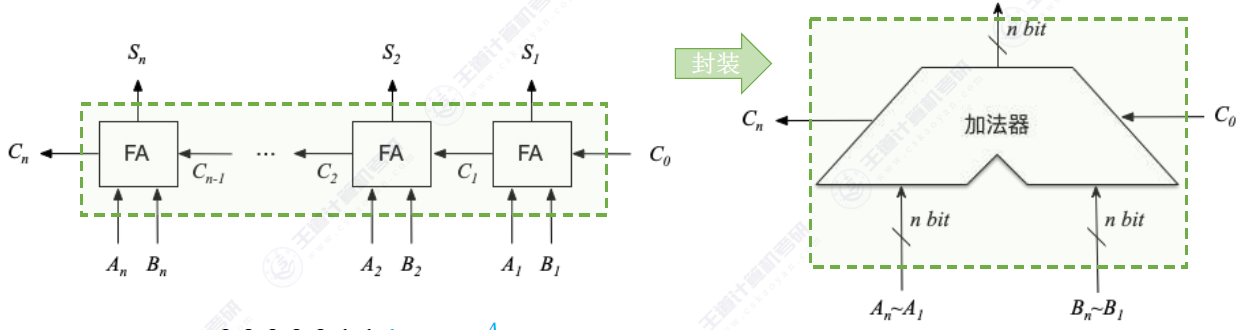
但是由于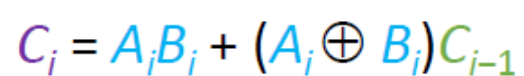
可知每一位的高位进位都依赖于低位的信号产出这就使得需要等待低位的运算结束才能进行高位的运算，这样的操作我们理解为串行操作，与之对应的时并行操作（需要CLA部件）。并行的加法器稍后讲解。
这里需要知道串行的加法器速率较慢
下图是并行进位的加法器
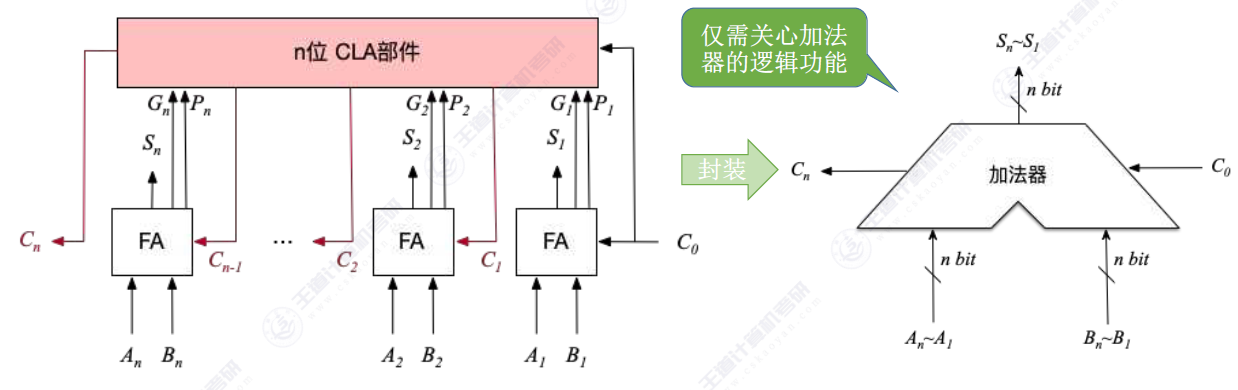
多出的CLA部件可以并行的计算出高位的进位但是电路较为复杂。一般就扩展到4位。
接下来我们的目光放到带标志位的加法器
为什么要带标志位？一般带哪些标志位？
首先解释为什么要带标志位？带标志位可以很快的得出此次加法的相关信息例如是否溢出是否借位运算结果的正负性。
一般带下面四个标志位
of溢出 1溢出0未溢出
sf符号标志 1负0正
zf零标志位 1为零 0不为零
cf无符号溢出 1溢出 0 未溢出
接下来介绍一下这几个常见标志位的运算逻辑表达式
有关于OF CF后面会详细讲解，这里解释一下sf它只需要取计算的最高位即可 zf需要采用或非电路，当全部为都为0时或电路输出0然后再非就输出1此时zf=1表示运算结果为0.
接下来介绍一下并位加法器
前面介绍过本为和采用异或来计算
而高位的进位
采用AB先与，或上AB异或与上低位进位，这里包括了进位的两种情况，本位都为1相加后需要进位，以及AB其中一个为1但是低位进位为1相加后也要进位。或者当AB都为0时不进位。
这里时串行进位加法器，我们可以采用一个电器电路CLA一下得出所有的进位然后直接就可以进行并行的加法计算
具体的逻辑推导如下
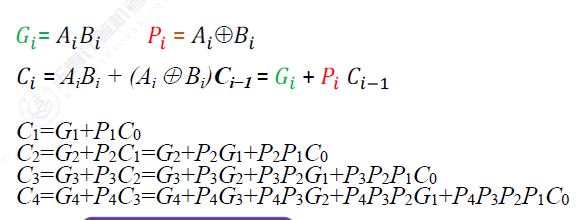
注意这里的每一个算术表达式都需要一个电路来实现，所以说就不太方便进行更深层次的套娃因为这样会非常耗费硬件。对应计算机成本也更高。
一般最多采取4为的CLA加法器。
算术逻辑单元ALU
主要了解其功能，
其实ALU更像是一个集合体加一个多路选择器
他这里里面所包含的操作一般都有其对印的电路或者代替电路，就比如前面所说的加法器
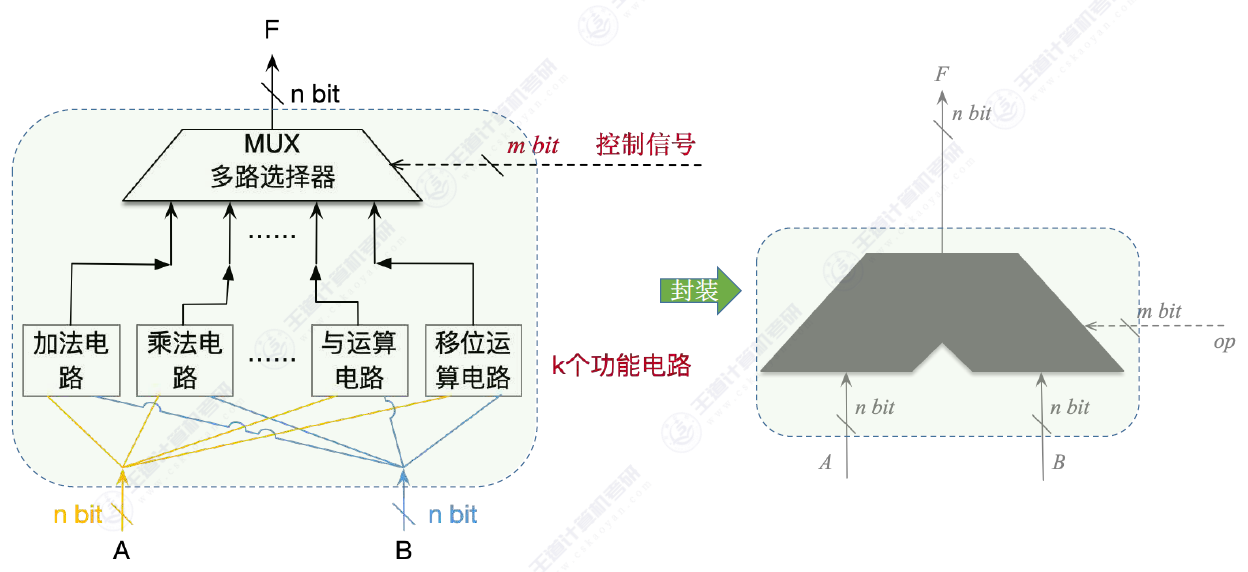
就如图所示它封装了好多功能在里面对外只暴露出少量的引脚。
其中最重要的一个考点就是多路选择器的位数，他需要曼满足对应的操作类型。
再有就是前面提到的几个常见的标志位
OF有符号溢出位 1表示溢出
SF正负标志位 1表示负
ZF零标志位 1表示结果为0 采用了或非门
CF 无符号溢出位 1表示溢出
)
