Pycharm的Terminal打开后默认是python环境，无法执行pip等命令，也没办法退出

解决方案

• 点击Settings -> Tools -> Terminal
  
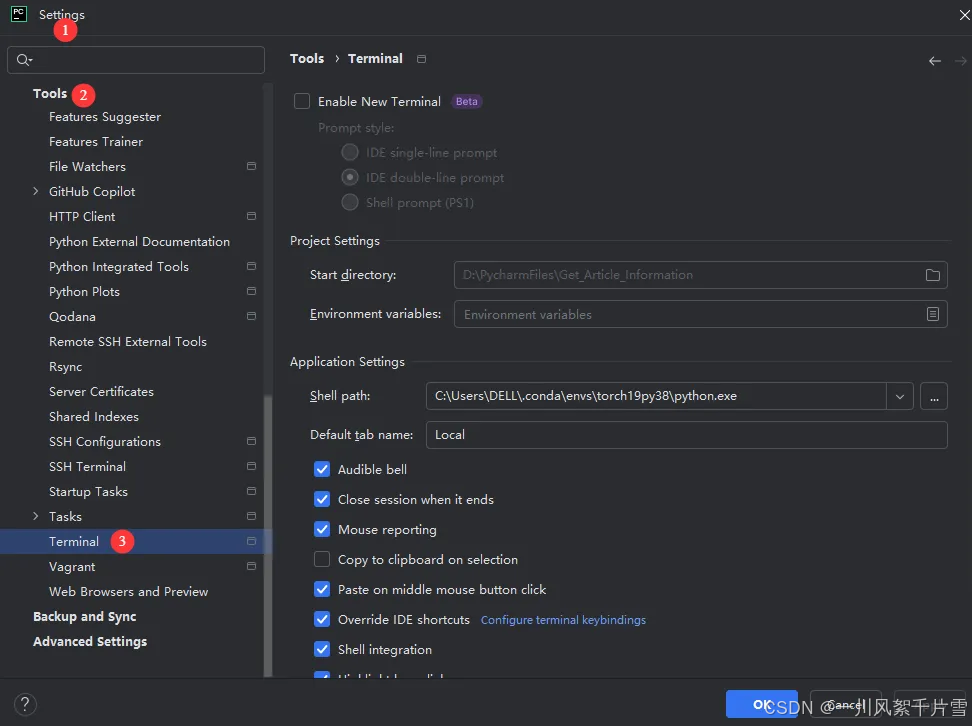
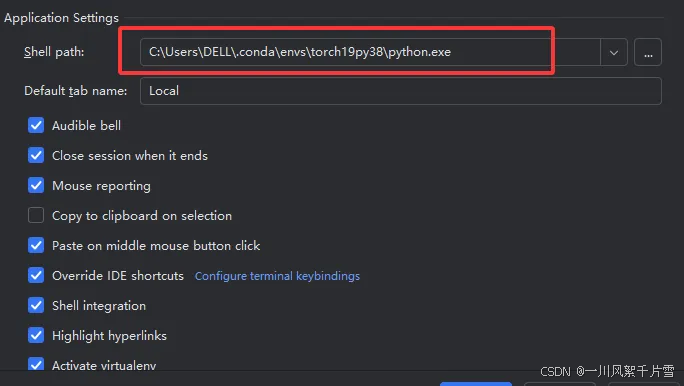
• 可以看到当前默认打开的是torch19py38环境中的python.exe（注：torch19py38是我自己命名的环境）
  
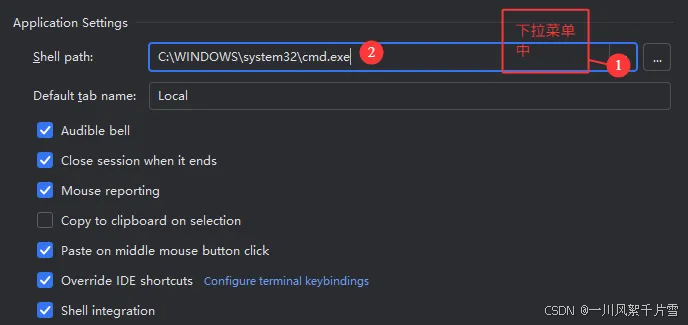
• 我们需要将上述环境修改为：cmd.exe，也就是默认打开的是cmd命令行
  
• 然后关闭之前的Terminal，再重新打开，可以看到成功进入了当前项目目录的cmd命令行
  
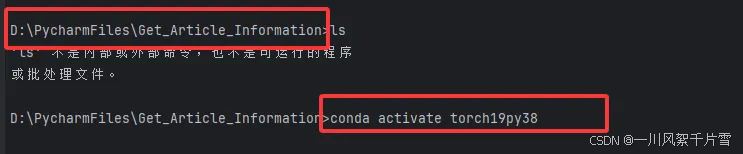
• 也可以通过上述命令激活任意的conda环境了
  
• 尝试在pycharm的Terminal中激活conda环境并使用pip安装包