一.栈 · stack

1.概念

栈 :

一种特殊的线性表 , 其只允许再固定的一段进行插入和删除元素操作
进行数据插入和删除操作的一段称为栈顶 ; 另一端称为栈底
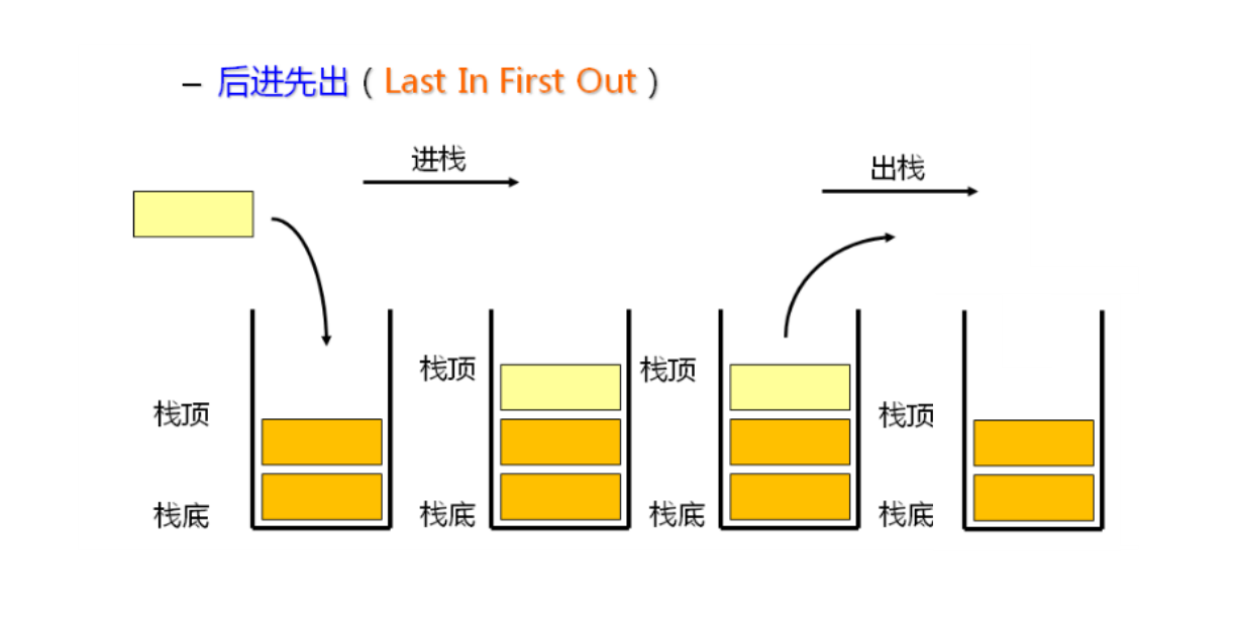
栈中的数据元素遵循 先进后出 原则(LIFO)
压栈 : 栈的插入操作叫做进栈或压栈或入栈 , 入数据在栈顶
出栈 : 栈的删除操作叫做出栈 , 出数据在栈顶

2.栈的主要方法

方法	功能
Stack()	构造一个空的栈
E push(E e)	将 e 入栈，并返回 e
E pop()	将栈顶元素出栈并返回
E peek()	获取栈顶元素
int size()	获取栈中有效元素个数
boolean empty()	检测栈是否为空

    public static void main(String[] args) {Stack<Integer> stack = new Stack<>();stack.push(11);stack.push(12);stack.push(13);stack.push(14);System.out.println(stack);System.out.println(stack.size());System.out.println(stack.peek());stack.pop();}

3.栈的模拟实现

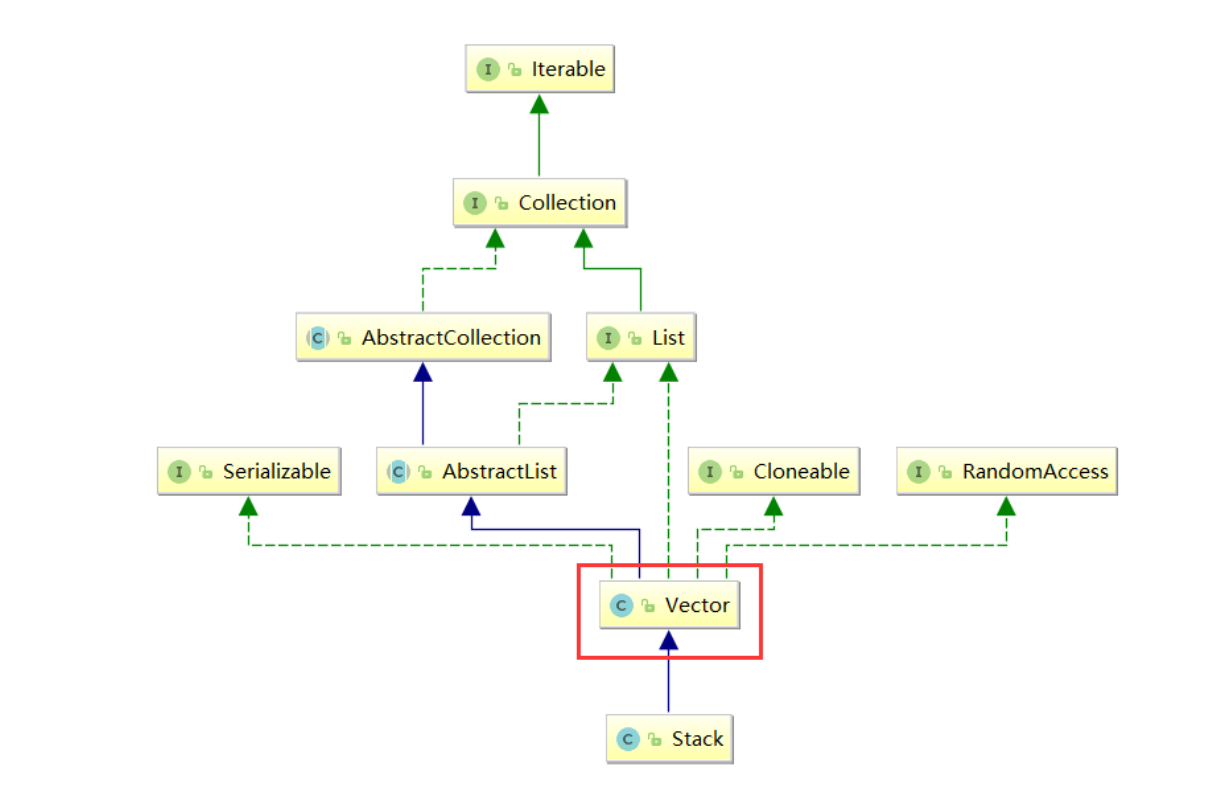
Stack 继承了 Vector(动态顺序表)

import java.util.Arrays;public class MyStack {public int[] elem;public int usedSize;public MyStack(){this.elem = new int[10];}public boolean isFull(){return this.elem.length == usedSize;}//将 元素 val 入栈 , 并返回public void push(int val){if(isFull()){//判满this.elem = Arrays.copyOf(elem,elem.length*2);//满了则扩大为原来的两倍}this.elem[usedSize++] = val;//后置++ , 先使用usedSize , 再+1}public boolean empty(){return usedSize == 0;//判断是否为空 , 空返回true , 非空返回false}public int pop(){//将栈顶元素取出 , 并返回if(empty()){throw new EmptyStackException();}else{int val = elem[usedSize-1];usedSize--;return val;}}public int peek(){//获取栈顶元素if(empty()){throw new EmptyStackException();}else{return elem[usedSize];}}}

public class EmptyStackException extends RuntimeException{public EmptyStackException() {super();}public EmptyStackException(String message) {super(message);}
}

测试:

public class Test {public static void main(String[] args) {MyStack myStack = new MyStack();myStack.push(11);myStack.push(12);myStack.push(13);myStack.push(14);System.out.println(myStack);//打印栈的元素System.out.println(myStack.pop());//打印栈顶的元素 , 并将栈顶元素取出System.out.println(myStack);System.out.println(myStack.peek());//打印栈顶的元素}
}

4.栈的应用场景

①改变元素序列

②将递归化为循环

// 递归方式
void printList(Node head) {if (null != head) {printList(head.next);System.out.print(head.val + " ");}
}// 循环方式
void printList(Node head) {if (null == head) {return;}Stack<Node> s = new Stack<>();// 将链表中的结点保存在栈中Node cur = head;while (null != cur) {s.push(cur);cur = cur.next;}// 将栈中的元素出栈while (!s.empty()) {System.out.print(s.pop().val + " ");}
}

③括号匹配问题

题目:

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。
有效字符串需满足：
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
每个右括号都有一个对应的相同类型的左括号

public boolean isValid(String s) {Stack<Character> stack = new Stack();for(int i = 0;i<s.length();i++){char c1 = s.charAt(i);if(c1 == '(' || c1 == '[' || c1 == '{'){stack.push(c1);}else {if(stack.empty()){return false;}char c2 = stack.peek();if(c1 == ')' && c2 == '('|| c1 == '}' && c2 == '{'|| c1 == ']' && c2 == '['){stack.pop();}else {return false;}}}if(!stack.empty()){return false;}return true;}

④栈的压入、弹出序列

题目:

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序
假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。
0<=pushV.length == popV.length <=1000
-1000<=pushV[i]<=1000
pushV 的所有数字均不相同

        public boolean IsPopOrder (int[] pushV, int[] popV) {Stack <Integer> stack = new Stack<>();int j = 0;for (int i = 0; i < pushV.length; i++) {stack.push(pushV[i]);while(!stack.empty()&&j < popV.length&&stack.peek() == popV[j]){stack.pop();j++;}}return stack.empty() ;}

⑤逆波兰表达式求值

中缀表达式求值

逆波兰表达式求值:

将这些字符从左到右依次放到栈中
其中数字放到栈中 , 遇到算数符号时 , 取出两个栈顶的元素
其中最上方的元素作为运算符的左操作数,下一个元素作为右操作数 , 再把得到的结果放回栈中
继续重复操作

题目:

给你一个字符串数组 tokens ，表示一个根据逆波兰表示法表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

注意：

有效的算符为 '+'、'-'、'*' 和 '/' 。
每个操作数（运算对象）都可以是一个整数或者另一个表达式。
两个整数之间的除法总是 向零截断 。
表达式中不含除零运算。
输入是一个根据逆波兰表示法表示的算术表达式。
答案及所有中间计算结果可以用 32 位 整数表示。

public boolean isoperation(String s){if(s.equals("+")||s.equals("-")||s.equals("*")||s.equals("/")){return true;}else {return false;}}public int evalRPN(String[] tokens) {Stack<Integer> stack = new Stack<>() ;for (String c:tokens) {if(!isoperation(c)){int x = Integer.parseInt(c);stack.push(x);}else {int val2 = stack.pop();int val1 = stack.pop();switch (c){case "+":stack.push(val1+val2);break;case "-":stack.push(val1-val2);break;case "*":stack.push(val1*val2);break;case "/":stack.push(val1/val2);break;}}}return stack.pop();}