P2052 [NOI2011] 道路修建
题目描述
在 W 星球上有 nnn 个国家。为了各自国家的经济发展,他们决定在各个国家之间建设双向道路使得国家之间连通。但是每个国家的国王都很吝啬,他们只愿意修建恰好 n−1n - 1n−1 条双向道路。
每条道路的修建都要付出一定的费用,这个费用等于道路长度乘以道路两端 的国家个数之差的绝对值。例如,在下图中,虚线所示道路两端分别有 222 个、444 个国家,如果该道路长度为 111,则费用为 1×∣2−4∣=21×|2 - 4|=21×∣2−4∣=2。图中圆圈里的数字表示国家的编号。
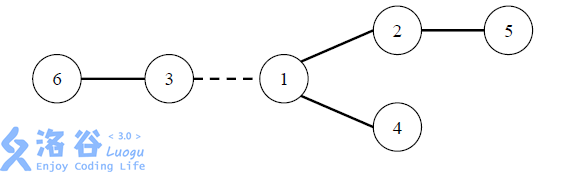
由于国家的数量十分庞大,道路的建造方案有很多种,同时每种方案的修建费用难以用人工计算,国王们决定找人设计一个软件,对于给定的建造方案,计算出所需要的费用。请你帮助国王们设计一个这样的软件。
输入格式
输入的第一行包含一个整数 nnn,表示 W 星球上的国家的数量,国家从 111 到 nnn 编号。
接下来 n−1n - 1n−1 行描述道路建设情况,其中第 iii 行包含三个整数 aia_iai,bib_ibi 和 cic_ici,表示第 iii 条双向道路修建在 aia_iai 与 bib_ibi 两个国家之间,长度为 cic_ici。
输出格式
输出一个整数,表示修建所有道路所需要的总费用。
输入输出样例 #1
输入 #1
6
1 2 1
1 3 1
1 4 2
6 3 1
5 2 1
输出 #1
20
说明/提示
对于 100%100\%100% 的数据,1≤ai,bi≤n1\leq a_i, b_i\leq n1≤ai,bi≤n,0≤ci≤1060\leq c_i\leq10^60≤ci≤106,2≤n≤1062\leq n\leq 10^62≤n≤106。
| 测试点编号 | n=n=n= |
|---|---|
| 111 | 222 |
| 222 | 101010 |
| 333 | 100100100 |
| 444 | 200200200 |
| 555 | 500500500 |
| 666 | 600600600 |
| 777 | 800800800 |
| 888 | 100010001000 |
| 999 | 10410^4104 |
| 101010 | 2×1042\times 10^42×104 |
| 111111 | 5×1045\times 10^45×104 |
| 121212 | 6×1046\times 10^46×104 |
| 131313 | 8×1048\times 10^48×104 |
| 141414 | 10510^5105 |
| 151515 | 6×1056\times 10^56×105 |
| 161616 | 7×1057\times 10^57×105 |
| 171717 | 8×1058\times 10^58×105 |
| 181818 | 9×1059\times 10^59×105 |
| 19,2019,2019,20 | 10610^6106 |
solution
任以一个节点为根节点,dfs 统计每一个子树 u 的 size 对于每条边 e 的长度为 w, 则该边的费用为 w * abs(n - 2 * size), 对所有边费用求和即可
代码
#include<iostream>
#include<algorithm>
#include "cstring"
#include "vector"using namespace std;/** P2052 [NOI2011] 道路修建* 题目大意: 一个有权无向连通图,要得到一颗树,使得费用最小,费用为树的边费用之和,边的费用为边的长度乘以边两端的节点数量之差。** 思路:* 任以一个节点为根节点,dfs 统计每一个子树 u 的 size 对于每条边 e 的长度为 l* 则该边的费用为 l * abs(n - 2 * size), 求和即可**/typedef long long ll;
typedef pair<int, int> pii;
const int N = 1e6 + 5;int n;
ll ans;
vector<pii> e[N];int dfs(int u, int p) {int siz = 1;for (auto [v, w]: e[u]) {if (v == p) continue;int siz_v = dfs(v, u);ans += 1ll * abs(n - 2 * siz_v) * w;siz += siz_v;}return siz;
}int main() {cin >> n;for (int i = 1, x, y, w; i < n; i++) {scanf("%d%d%d", &x, &y, &w);e[x].emplace_back(y, w);e[y].emplace_back(x, w);}dfs(1, 0);cout << ans << endl;return 0;
}
结果







》免费中文翻译 (第6章) --- scripts and projects)





)






的详细分析与实现)