前置说明
linux服务器版本:CentOS10
ollama版本:v0.11.6
下载安装包
下载安装包
官网地址:Ollama
下载地址:Download Ollama
选择linux平台,由于使用官网提供的脚本直接安装容易失败,这里选择手动下载安装包进行安装,直接去github下载安装包:https://github.com/ollama/ollama/tags
选择对应安装的版本,这里以v0.11.6为例,选择对应平台的安装包下载
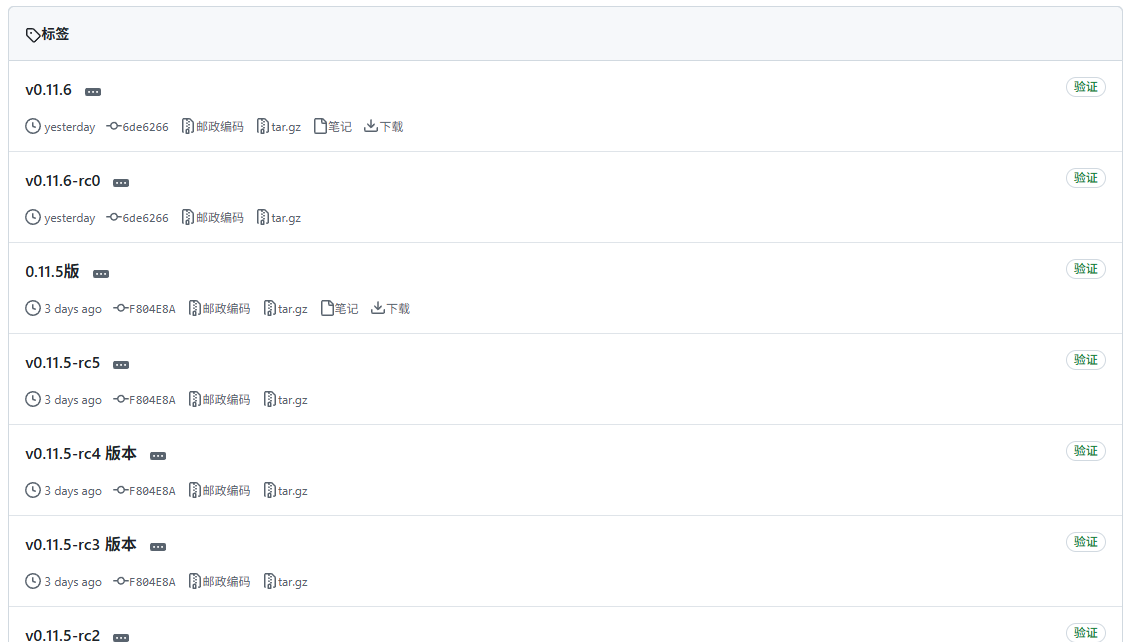
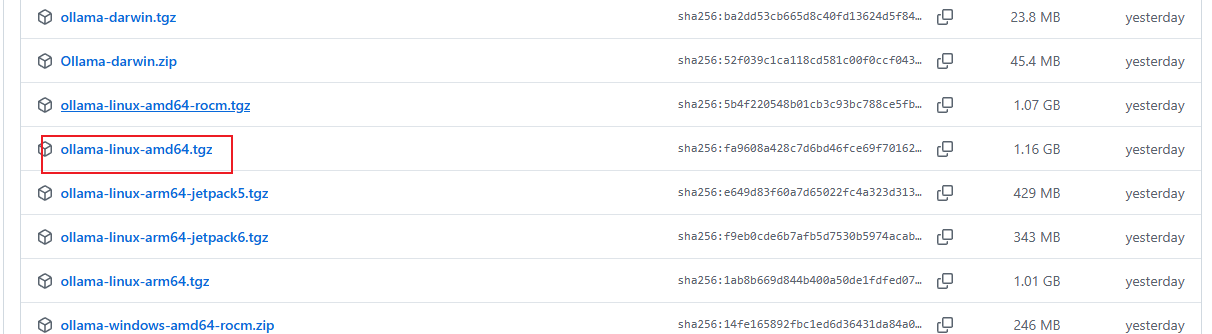
下载好安装包之后上传到服务器,或者直接使用以下命令将安装包下载到服务器
wget https://github.com/ollama/ollama/releases/download/v0.11.6/ollama-linux-amd64.tgz
解压
压缩包直接解压到/usr目录下,可以省去配置环境变量的步骤
tar -xvf ollama-linux-amd64.tgz -C /usr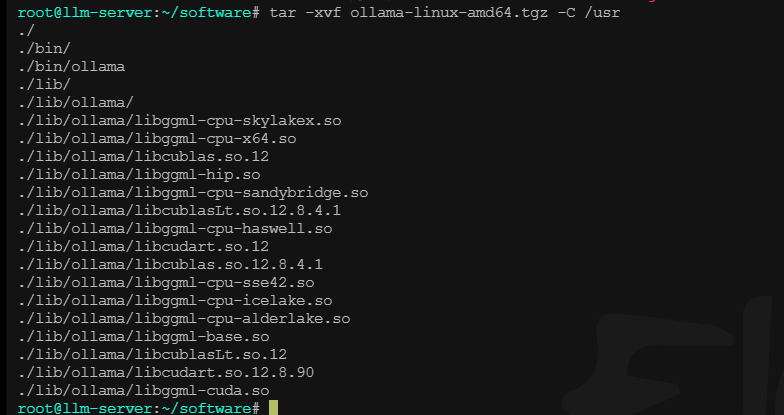
查看版本号
ollama -v
创建用户组
useradd -r -s /bin/false -U -m -d /usr/share/ollama ollama
usermod -a -G ollama $(whoami)关闭防火墙
systemctl stop firewalld.service
systemctl disable firewalld.service添加为系统服务
vim /etc/systemd/system/ollama.service内容如下
[Unit]
Description=Ollama Service
After=network-online.target[Service]
ExecStart=/usr/bin/ollama serve
User=ollama
Group=ollama
Restart=always
RestartSec=3
Environment="PATH=$PATH"
Environment="OLLAMA_HOST=0.0.0.0:11434"[Install]
WantedBy=multi-user.target启动ollama 服务、设置开机自启
systemctl daemon-reload
systemctl enable ollama
systemctl start ollama查看服务运行状态
systemctl status ollama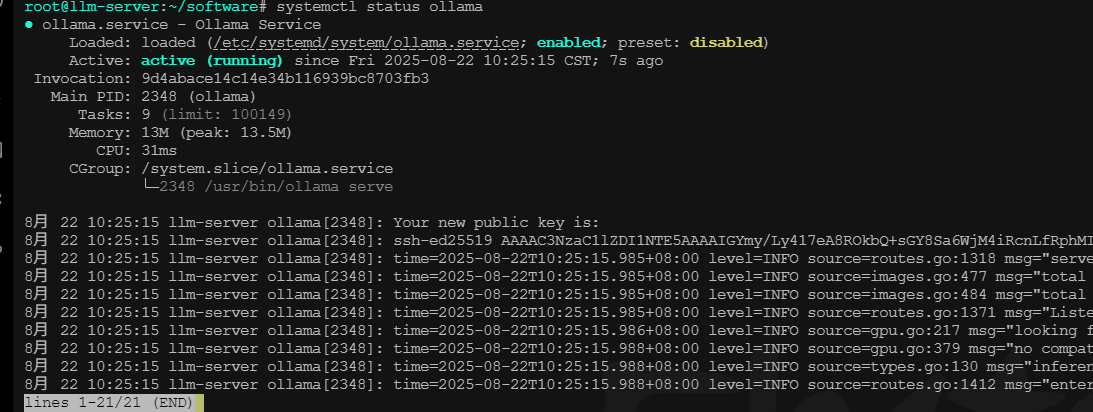






之 量化对比余弦——仙盟创梦IDE)



)
及其实例化程序,模拟了时间的设置、显示和自动流逝功能,类似一个简易电子时钟。)




- 基本类型 PART1)


