Problem - D - Codeforces

题目：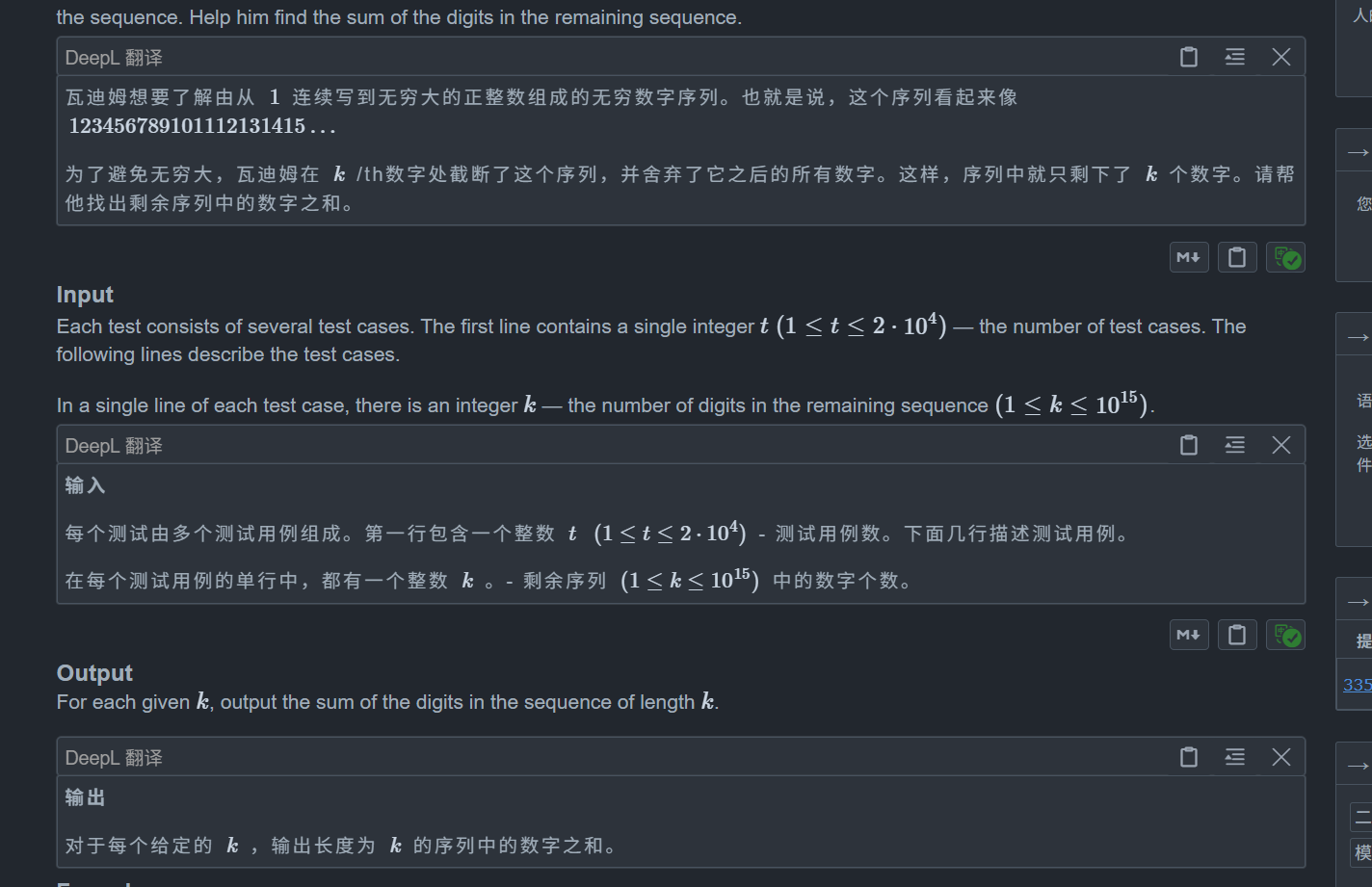

思路：

数位DP + 数论

题目让我们求这个无限序列 123456789101112.... 的前 k 个数的数位和

题目看起来很不好求，事实上确实是这样的

我们可以先从简单问题开始

问题①. 求 k 位置对应着第几个数

那么显然我们很好求出这个数，首先每一位的数都有   个数位，比如两个位数就有 9 * 10 个数，每一个数都有两位，那么就是有 9 * 10 * 2 位

因此我们可以不断计算求出一个 wei，其代表 k 处于有 wei 位数字，那么现在求 k 是其中的第几个，那么此时一个数要占据 wei 位，所以 k 个数就能往后 k / wei 个数了，但是要注意我们从下标 0 开始数的，因此 k 要减一，防止多计算了

所以 k 处于的数就是 ，其中 num 代表往后几位

那么对于这个数也很好求了，我们直接转为字符串计算即可

问题②. 计算 1 ~ n 的所有数位和

这个问题我们可以使用数位dp来解决，虽然也能用过其他的递归+数学解决，但是练习数位dp也是挺好的

我们定义 f[i] 为第 i 位能所有数的数位和，g[i] 为第 i 位时为能构成的数的数量，然后套板子即可，具体实现看代码，还是很简单的

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());int getans(int n)
{string a = to_string(n);int m = a.size();vector<int> f(m,-1),g(m,-1);auto dfs = [&](auto && self,int now,int lim,int zero)->pair<int,int>{if(now == m){return {0,1};}if(!lim && !zero && f[now] != -1) return {f[now],g[now]};int mx = lim ? (a[now] - '0') : 9;int res = 0,cnt = 0;for (int i = 0; i <= mx; i++){auto [ans,num] = self(self,now+1,lim && i == mx,zero && i == 0);res += ans + num * i;cnt += num;}   if(!lim && !zero){f[now] = res;g[now] = cnt;}return {res,cnt};};return dfs(dfs,0,1,1).first;
}   void solve()
{int k;cin >> k;int wei = 1;while (wei * 9 * pow(10, wei - 1) <= k){k -= wei * 9 * pow(10, wei - 1);wei++;}int num = (k - 1) / wei; // 往后多少个数，减一防止多偏移，如 wei = 2，k = 2，那么此时如果不减则 k / wei = 1，即往后一位，算出来位 11，实际上是 10int n = pow(10, wei - 1) + num;string s = to_string(n);int ans = 0;for (int i = 0; i <= (k - 1) % wei; i++) //(k - 1) % wei 第 n 个数其包含了多少位{ans += s[i] - '0';}ans += getans(n - 1);cout << ans << endl;
}signed main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int t = 1;cin >> t;while (t--){solve();}return 0;
}