1 聚类算法
-
聚类算法:
- 是一种无监督学习算法,它不需要预先知道数据的类别信息,而是根据样本之间的相似性,将样本划分到不同的类别中;
- 不同的相似度计算方法,会得到不同的聚类结果,常用的相似度计算方法有欧式距离法;
- 其目的是在没有先验知识的情况下,自动发现数据集中的内在结构和模式;
-
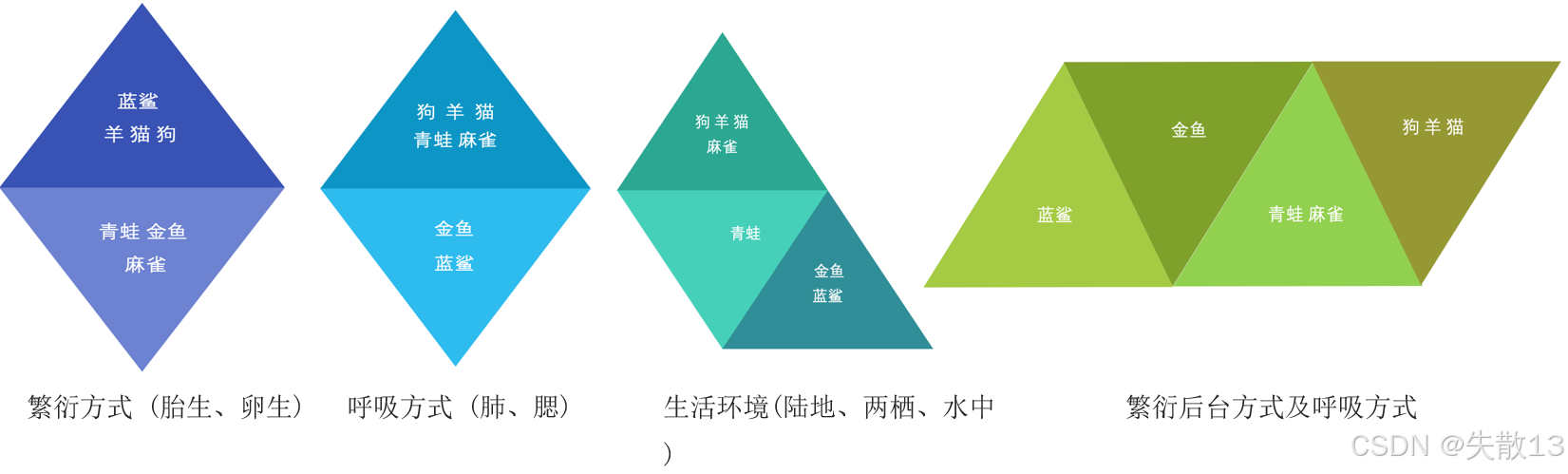
使用不同的聚类准则,产生的聚类结果不同;
-
聚类算法在现实生活中的应用十分广泛,涵盖多个领域:
-
商业领域:可用于用户画像和广告推荐,通过分析用户的行为、偏好等数据,将用户进行聚类,从而为不同类别的用户推送更精准的广告;还能进行基于位置信息的商业推送,根据用户的地理位置等信息进行分类推送;
-
信息处理领域:可实现新闻聚类和筛选排序,将相似的新闻归为一类,方便用户阅读和筛选;在搜索引擎方面,可用于流量推荐和恶意流量识别,提高搜索结果的质量和安全性;
-
图像和生物领域:在图像方面,可进行图像分割、降维和识别;在生物方面,可用于离群点检测(如信用卡异常消费检测)以及发掘相同功能的基因片段等;
-
-
聚类算法主要有以下两种分类方式:
-
根据聚类颗粒度分类:
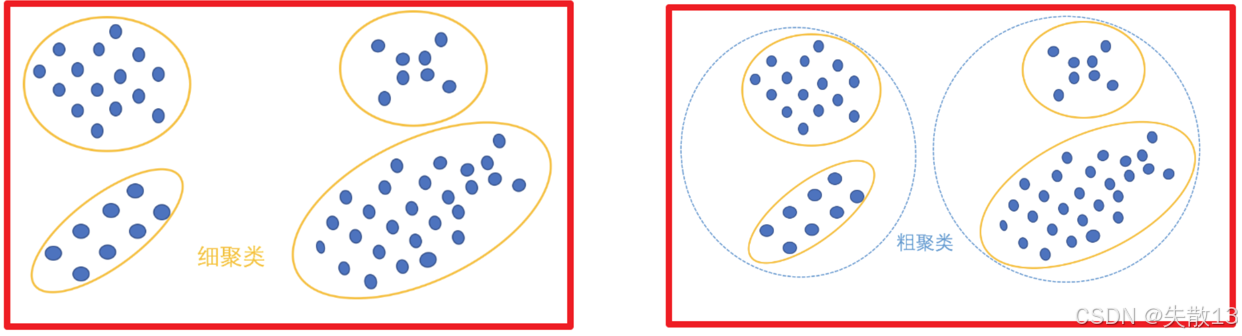
- 细聚类:将数据划分成更细致的类别,每个类别包含的数据点相对较少且更具针对性
- 粗聚类:将数据划分成较粗的类别,每个类别包含的数据点相对较多,概括性更强
-
根据实现方法分类:
- K-means:按照质心分类,是一种通用且普遍使用的聚类算法
- 层次聚类:对数据进行逐层划分,直到达到聚类的类别个数
- DBSCAN聚类:是一种基于密度的聚类算法,能够发现任意形状的聚类
- 谱聚类:是一种基于图论的聚类算法,通过构建样本的相似性矩阵,将聚类问题转化为图的划分问题
-
2 API&Kmeans算法
-
API:
sklearn.cluster.KMeans(n_clusters=8)- 参数:
n_clusters,整型,缺省值为 8,用于指定开始的聚类中心数量,即最终生成的聚类数,也就是产生的质心(centroids)数; - 方法:
estimator.fit(x):用于对数据x进行训练,计算聚类中心;estimator.predict(x):用于预测数据x中每个样本所属的类别;estimator.fit_predict(x):该方法的作用是计算聚类中心并预测每个样本属于哪个类别,相当于先调用fit(x),然后再调用predict(x);
- 参数:
-
例:随机创建不同二维数据集作为训练集,并结合k-means算法将其聚类,尝试分别聚类不同数量的簇,并观察聚类效果
-
导包:
# 0.导包 from sklearn.datasets import make_blobs import matplotlib.pyplot as plt from sklearn.cluster import KMeans # 导入KMeans聚类算法 from sklearn.metrics import silhouette_score # 导入轮廓系数评估指标 -
构建数据集:
# 1.构建数据集 # 使用make_blobs生成4个聚类中心的二维数据 x,y=make_blobs(n_samples=1000, # 生成1000个样本点n_features=2, # 每个样本有2个特征(便于可视化)centers=[[-1,-1],[4,4],[8,8],[2,2,]], # 指定4个聚类中心的坐标cluster_std=[0.4,0.2,0.3,0.2] # 指定每个聚类的标准差(数据离散程度)) plt.figure() # 绘制散点图,x[:,0]为第一特征,x[:,1]为第二特征 plt.scatter(x[:,0],x[:,1]) plt.show()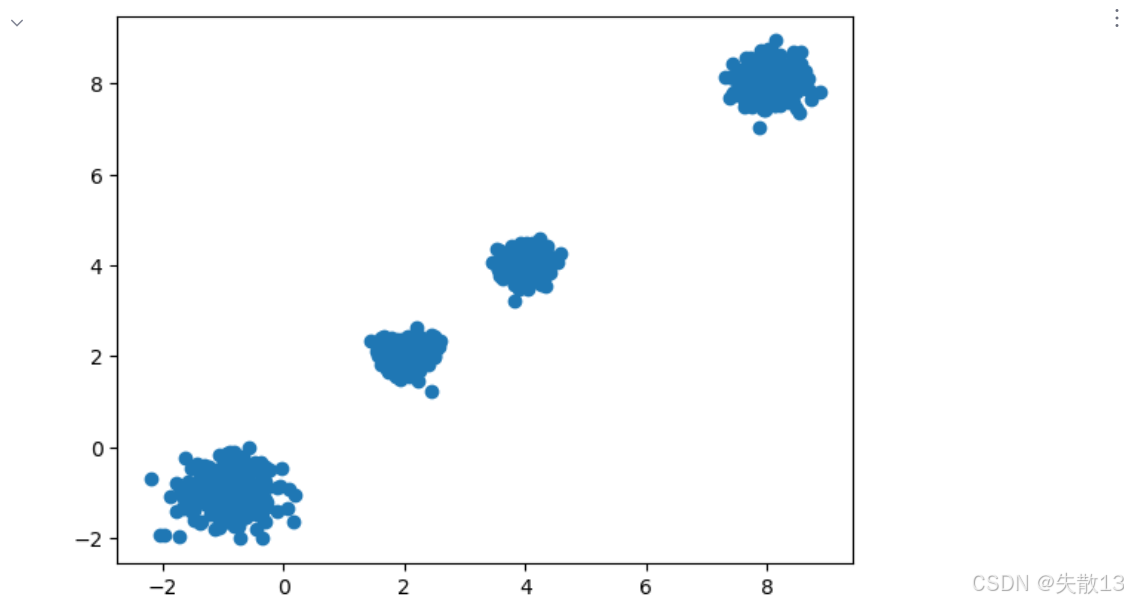
-
模型训练预测:
# 2.模型训练预测 # 创建KMeans模型实例,指定聚类数量为4(与我们生成数据时的中心数一致) model=KMeans(n_clusters=4) # 训练模型并对数据进行预测,返回每个样本的聚类标签 # fit_predict()等价于先调用fit()训练模型,再调用predict()预测标签 y_prd=model.fit_predict(x)plt.figure() # 按预测的聚类标签着色绘制散点图,不同聚类会显示不同颜色 plt.scatter(x[:,0],x[:,1],c=y_prd) plt.show()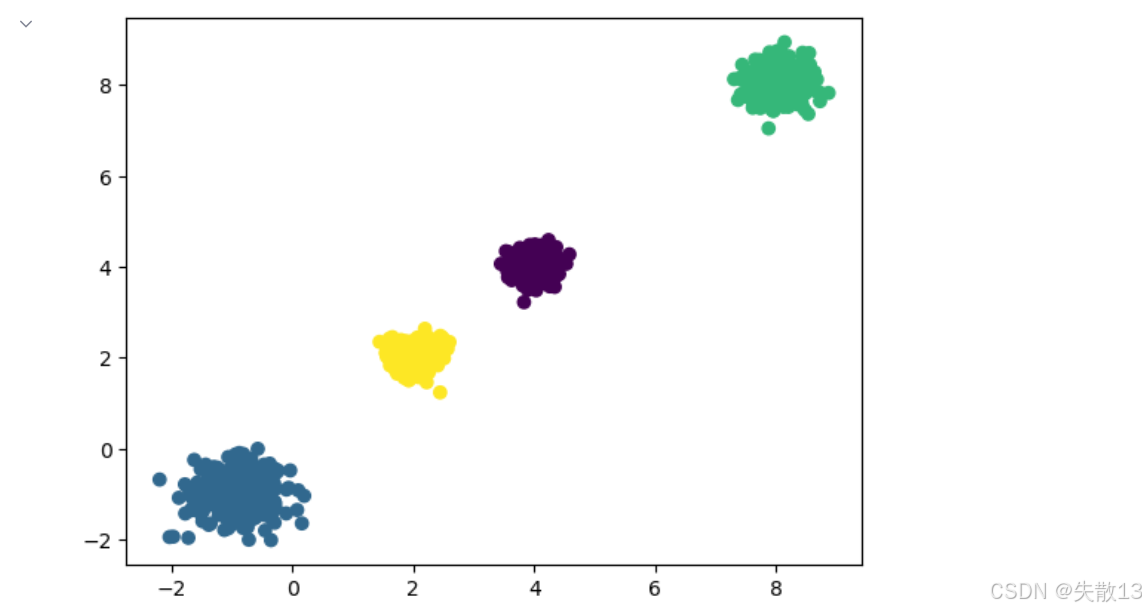
-
模型评估:
# 3.评估 # 使用轮廓系数(silhouette_score)评估聚类效果 # 轮廓系数取值范围为[-1,1],越接近1表示聚类效果越好 # 输入参数为原始数据x和预测的聚类标签y_prd print(silhouette_score(x,y_prd))
-
3 Kmeans实现流程
3.1 概述
-
KMeans算法的实现主要分为以下几个步骤:
- 确定聚类数K:首先需要事先确定常数K,K表示最终想要得到的聚类类别数;
- 选择初始聚类中心:随机从数据集中选择K个样本点,将它们作为初始的聚类中心;
- 分配样本到最近聚类:计算每个样本到这K个聚类中心的距离,然后将每个样本分配到距离最近的那个聚类中心所对应的类别中;
- 更新聚类中心并迭代:根据每个类别中的所有样本点,重新计算该类别的新聚类中心点(通常是该类别所有样本点的均值)。如果新计算出的聚类中心点与原来的聚类中心点相同,那么聚类过程停止;否则,重新进行步骤2和步骤3,直到聚类中心不再发生变化为止;
-
下面通过图形化的方式展示KMeans算法的迭代过程:
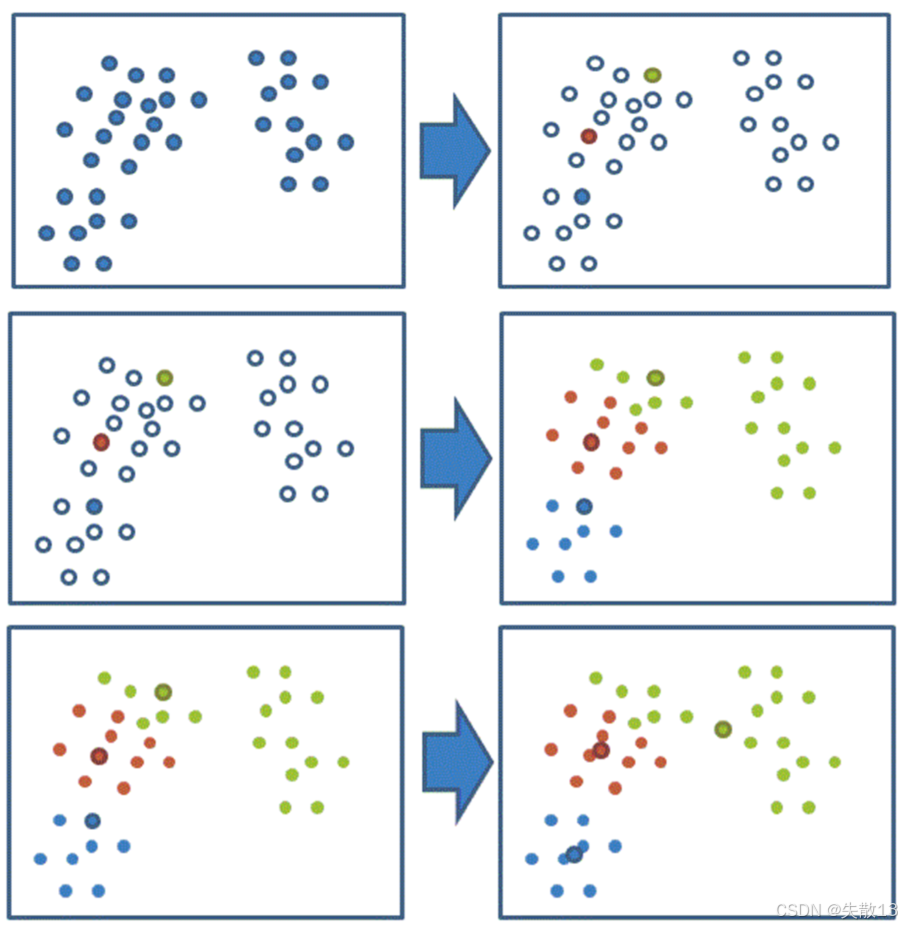
-
初始状态:首先随机选择了两个初始聚类中心(图中可能用不同颜色或标记表示)
-
第一次迭代:根据初始聚类中心,将数据点分配到最近的聚类中心,形成两个初始的聚类
-
后续迭代:重新计算每个聚类的中心点,然后再次将数据点分配到新的聚类中心,不断重复这个过程
-
收敛状态:经过多次迭代后,聚类中心不再发生明显变化,算法收敛,得到最终的聚类结果
-
3.2 例
-
数据准备:已知数据集如下,包含 15 个数据点(P1 - P15),每个数据点有两个特征(X 值和 Y 值)。这些数据点将作为输入,用于后续的 KMeans 聚类过程;
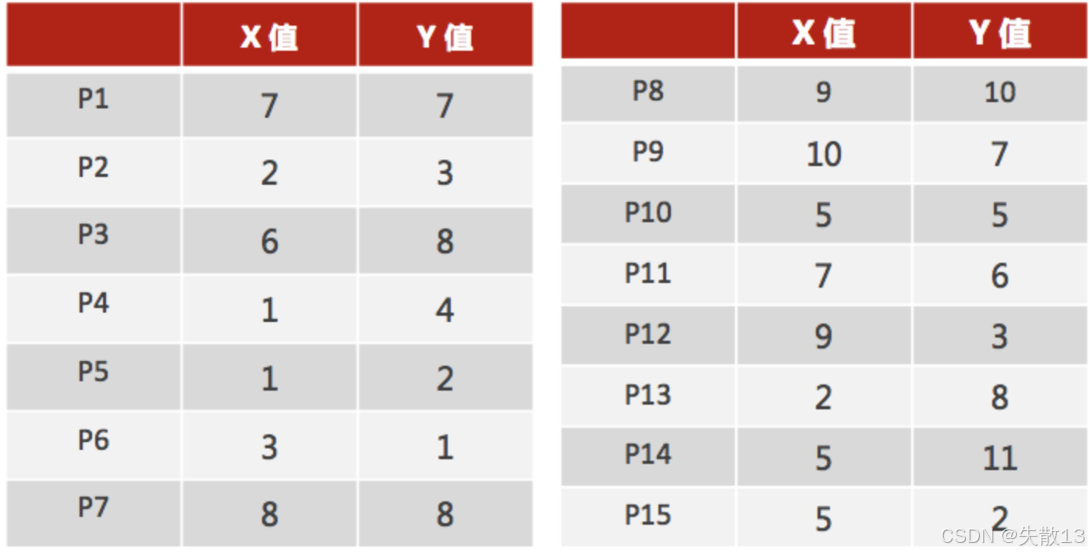
-
选择初始聚类中心
-
选择初始聚类中心:在这个例子中,随机选择了两个数据点 P1(7, 7)和 P2(2, 3)作为初始的聚类中心;
-
距离计算公式:使用欧几里得距离(Euclidean distance)来计算数据点之间的距离。公式为:
d=∑i=1k(xi−yi)2 d=\sqrt{\sum_{i = 1}^{k}(x_i - y_i)^2} d=i=1∑k(xi−yi)2 -
对于二维数据,公式可以简化为:
d=(xn−x1)2+(yn−y1)2 d=\sqrt{(x_n - x_1)^2+(y_n - y_1)^2} d=(xn−x1)2+(yn−y1)2- 其中,(xn,yn)(x_n, y_n)(xn,yn) 和 (x1,y1)(x_1, y_1)(x1,y1) 分别是两个数据点的坐标;
-
数据点分布:下图展示了所有数据点在二维平面上的分布情况,其中 P1 和 P2 被标记为初始聚类中心
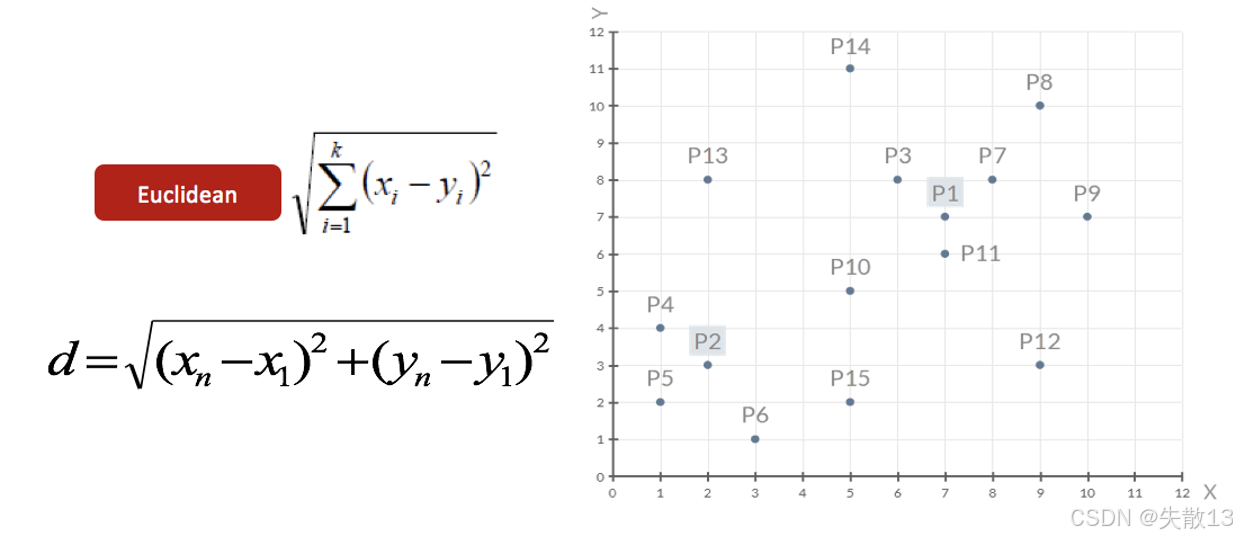
-
-
分配样本到最近聚类
-
计算距离并分配类别:对于每个数据点,计算其到两个初始聚类中心(P1 和 P2)的距离,并将数据点分配到距离较近的聚类中心所在的类别。例如:
- P3 到 P1 的距离为 1.41,到 P2 的距离为 6.40,所以 P3 被分配到 P1 所在的类别;
- P4 到 P1 的距离为 6.71,到 P2 的距离为 1.41,所以 P4 被分配到 P2 所在的类别;
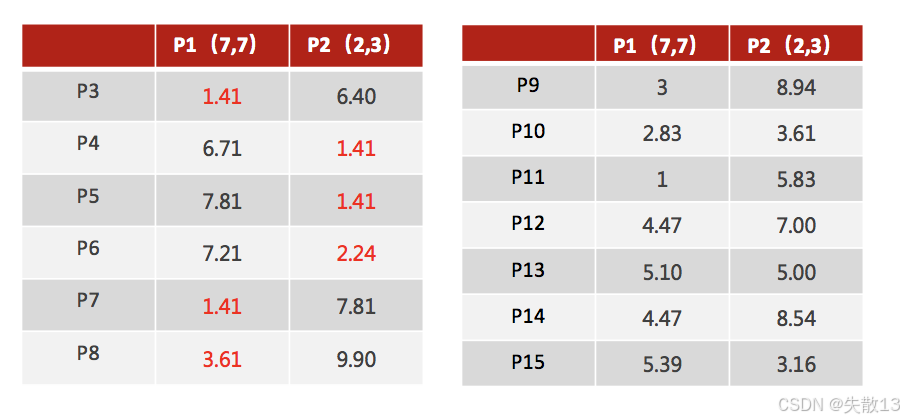
-
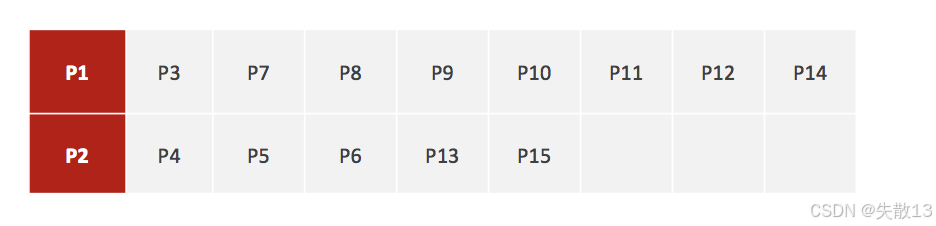
聚类结果:经过计算和分配,得到了两个初始的聚类,分别以 P1 和 P2 为中心。其中:
- P1 所在的聚类包含 P3、P7、P8、P9、P10、P11、P12、P14;
- P2 所在的聚类包含 P4、P5、P6、P13、P15;
-
-
更新聚类中心
-
重新计算聚类中心:根据上一步得到的两个聚类,重新计算每个聚类的新中心。新中心的计算方法是该聚类中所有数据点的 X 值和 Y 值的平均值;
- 对于 P1 所在的聚类,新中心 P1′P_1'P1′ 的 X 值为 (7+6+8+9+5+7+9+5)/8=7.3(7 + 6 + 8 + 9 + 5 + 7 + 9 + 5) / 8 = 7.3(7+6+8+9+5+7+9+5)/8=7.3,Y 值为 (7+8+8+10+5+6+3+11)/8=7.2(7 + 8 + 8 + 10 + 5 + 6 + 3 + 11) / 8 = 7.2(7+8+8+10+5+6+3+11)/8=7.2,即 P1′=(7.3,7.2)P_1' = (7.3, 7.2)P1′=(7.3,7.2);
- 对于 P2 所在的聚类,新中心 P2′P_2'P2′ 的 X 值为 (2+1+1+3+2+5)/6=1.8(2 + 1 + 1 + 3 + 2 + 5) / 6 = 1.8(2+1+1+3+2+5)/6=1.8,Y 值为 (3+4+2+1+8+2)/6=4.6(3 + 4 + 2 + 1 + 8 + 2) / 6 = 4.6(3+4+2+1+8+2)/6=4.6,即 P2′=(1.8,4.6)P_2' = (1.8, 4.6)P2′=(1.8,4.6);
-
数据点分布:图中展示了更新后的聚类中心 P1′P_1'P1′ 和 P2′P_2'P2′ 在二维平面上的位置;
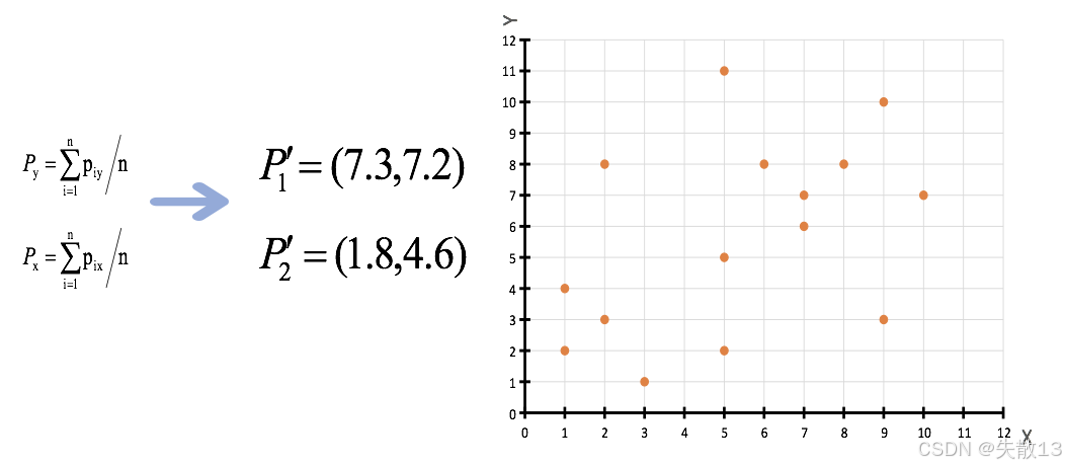
-
-
判断是否收敛
-
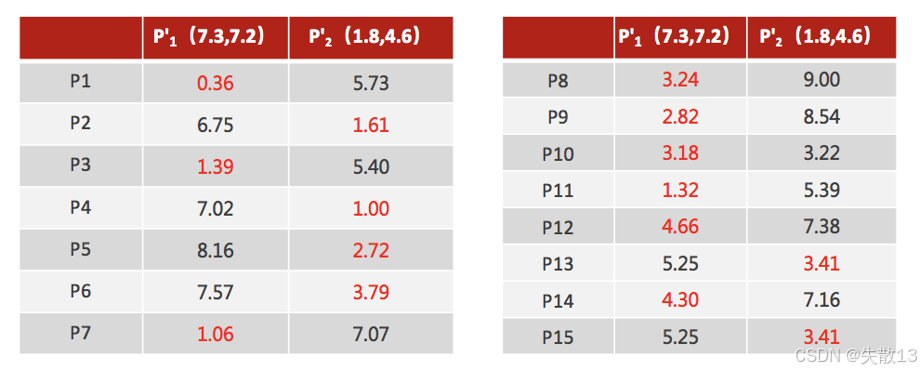
计算新距离并重新分配类别:使用更新后的聚类中心 P1′P_1'P1′ 和 P2′P_2'P2′,再次计算每个数据点到这两个中心的距离,并重新分配类别。例如:
- P1 到 P1′P_1'P1′ 的距离为 0.36,到 P2′P_2'P2′ 的距离为 5.73,所以 P1 被分配到 P1′P_1'P1′ 所在的类别;
- P2 到 P1′P_1'P1′ 的距离为 6.75,到 P2′P_2'P2′ 的距离为 1.61,所以 P2 被分配到 P2′P_2'P2′ 所在的类别;

-
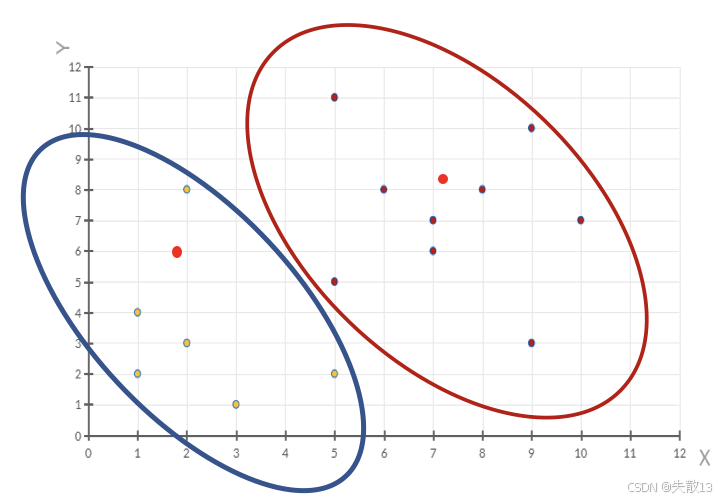
判断是否收敛:
- 比较新的聚类中心与原来的聚类中心,如果新的聚类中心与原来的聚类中心相同(质心不再移动),则聚类过程结束;
- 否则,需要重新进行第二步和第三步,直到聚类中心不再发生变化为止;
- 在这个例子中,经过判断,新的聚类中心与原来的聚类中心不同,所以需要重复上述步骤,开始新一轮迭代;
-
4 模型评估方法
4.1 SSE聚类评估指标
-
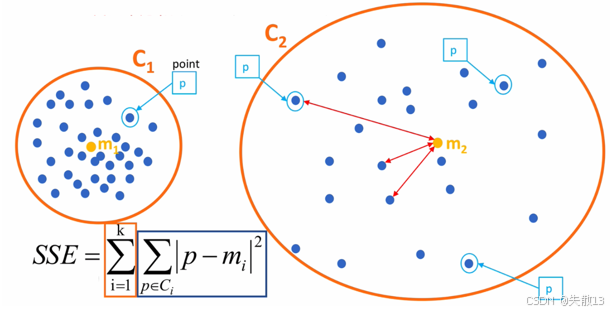
误差平方和SSE(The sum of squares due to error)。SSE公式:
SSE=∑i=1k∑p∈Ci∣p−mi∣2 SSE = \sum_{i = 1}^{k}\sum_{p \in C_i} |p - m_i|^2 SSE=i=1∑kp∈Ci∑∣p−mi∣2- 其中:CiC_iCi 表示簇、kkk 表示聚类中心的个数、ppp 表示某个簇内的样本、mmm 表示质心点
-
含义:
- SSE 越小,表示数据点越接近它们的中心,聚类效果越好;
- 下图通过两个簇 C1C_1C1 和 C2C_2C2 的示例,展示了 SSE 的计算方式,即每个数据点到其所在簇质心的距离的平方和;
-
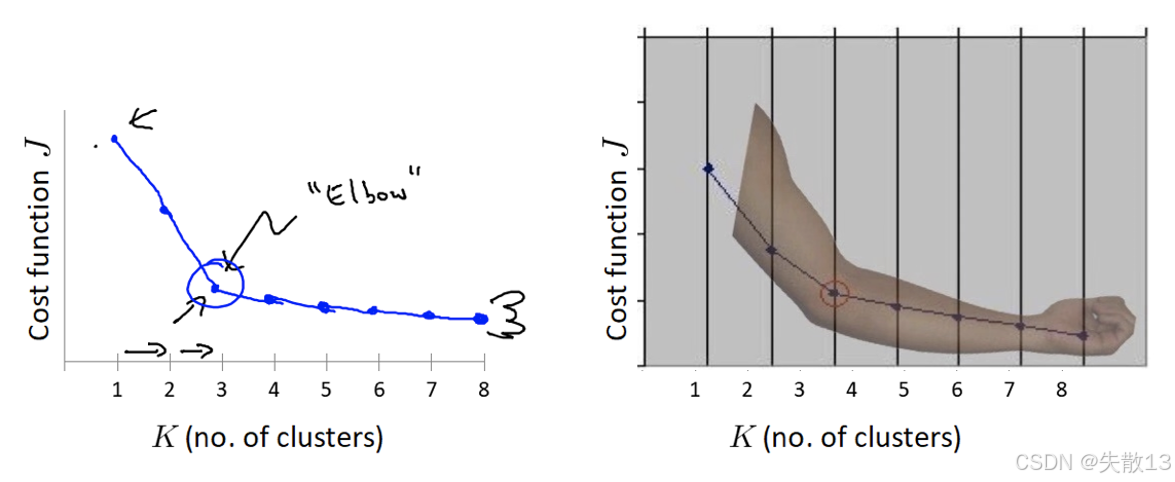
**“肘”方法(Elbow method)**通过 SSE 确定聚类数 n_clustersn\_clustersn_clusters 的值。步骤:
- 对于有 nnn 个点的数据集,迭代计算 kkk 从 1 到 nnn,每次聚类完成后计算 SSE
- SSE 会逐渐变小,因为每个点都是它所在簇中心本身
- SSE 变化过程中会出现一个拐点,当下降率突然变缓时,此时的 kkk 即为最佳的 n_clustersn\_clustersn_clusters 值
- 在决定什么时候停止训练时,肘形判据同样有效,数据通常有更多的噪音,在增加分类无法带来更多回报时,停止增加类别
-
图示:左侧的图展示了随着 kkk 的增加,SSE 的变化曲线,其中的拐点(“Elbow”)即为最佳的 kkk 值;右侧的图通过手臂的形状形象地展示了肘形判据的概念;
4.2 SC聚类评估指标
-
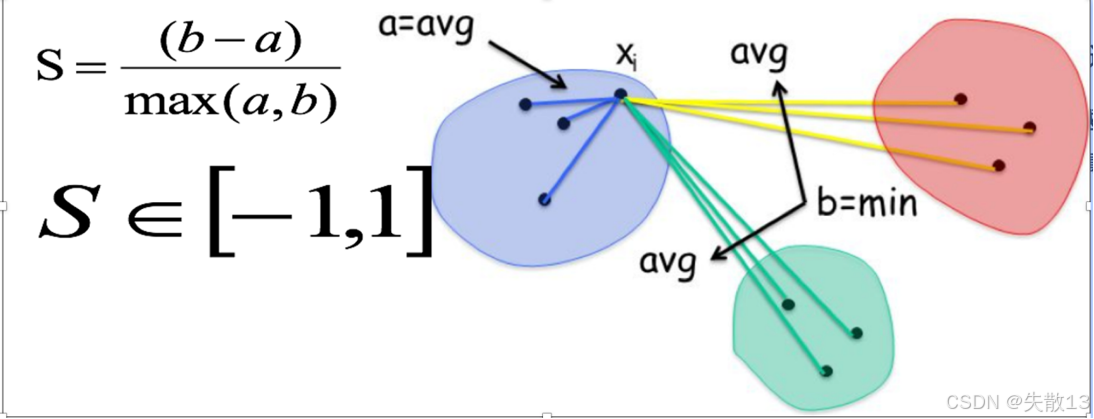
SC轮廓系数法(Silhouette Coefficient)的考虑因素:轮廓系数法考虑簇内的内聚程度(Cohesion)和簇外的分离程度(Separation);
-
计算过程:
- 计算每一个样本 iii 到同簇内其他样本的平均距离 aia_iai,该值越小,说明簇内的相似程度越大;
- 计算每一个样本 iii 到最近簇 jjj 内的所有样本的平均距离 bijb_{ij}bij,该值越大,说明该样本越不属于其他簇 jjj;
- 根据公式 S=b−amax(a,b)S = \frac{b - a}{max(a, b)}S=max(a,b)b−a 计算该样本的轮廓系数;
- 计算所有样本的平均轮廓系数;
-
取值范围:轮廓系数的范围为 [−1,1][-1, 1][−1,1],SC 值越大聚类效果越好;
-
图示:图中展示了样本 xix_ixi 到同簇内其他样本的平均距离 aaa 和到最近簇内所有样本的平均距离 bbb,并通过公式计算轮廓系数;
4.3 CH聚类评估指标
-
考虑因素:CH 系数(Calinski-Harabasz Index)考虑簇内的内聚程度、簇外的离散程度以及质心的个数。
-
公式:
CH(k)=SSBSSW⋅m−kk−1 CH(k) = \frac{SSB}{SSW} \cdot \frac{m - k}{k - 1} CH(k)=SSWSSB⋅k−1m−k- 其中:
-
SSW=∑i=1m∥xi−Cpi∥2SSW = \sum_{i = 1}^{m} \|x_i - C_{pi}\|^2SSW=∑i=1m∥xi−Cpi∥2,相当于 SSE,是簇内距离,表示簇内的内聚程度,越小越好。CpiC_{pi}Cpi 表示质心,xix_ixi 表示某个样本;
-
SSB=∑j=1knj∥Cj−Xˉ∥2SSB = \sum_{j = 1}^{k} n_j \|C_j - \bar{X}\|^2SSB=∑j=1knj∥Cj−Xˉ∥2,是簇间距离,表示簇与簇之间的分离程度,越大越好。CjC_jCj 表示质心,Xˉ\bar{X}Xˉ 表示质心与质心之间的中心点,njn_jnj 表示样本的个数;
-
mmm 表示样本数量,kkk 表示质心个数;
-
- 其中:
-
评估标准:类别内部数据的距离平方和越小越好,类别之间的距离平方和越大越好,聚类的种类数越少越好。
4.4 代码
-
导包:
# 0.导包 import os # 设置OpenMP线程数为1,避免多线程冲突(某些环境下KMeans可能出现的警告) os.environ["OMP_NUM_THREADS"]="1" from sklearn.datasets import make_blobs # 用于生成模拟聚类数据 import matplotlib.pyplot as plt from sklearn.cluster import KMeans # 导入KMeans聚类算法 # 导入两种聚类评估指标:Calinski-Harabasz指数和轮廓系数 from sklearn.metrics import calinski_harabasz_score,silhouette_score -
构建数据集:
# 1.构建数据集 # 生成1000个样本的二维数据,包含4个真实聚类中心 # centers参数指定真实聚类中心坐标,cluster_std指定每个聚类的标准差(数据离散程度) x,y=make_blobs(n_samples=1000,n_features=2,centers=[[-1,-1],[4,4],[8,8],[2,2,]],cluster_std=[0.4,0.2,0.3,0.2]) -
使用肘部法确定最佳k值:
# 使用肘部法(Elbow Method)确定最佳k值 # 存储不同k值对应的SSE(误差平方和) temp_list = [] # 迭代测试k从1到99的情况 for k in range(1,100):# 创建KMeans模型,n_clusters=k表示聚类数为k,n_init='auto'自动选择初始中心数量model = KMeans(n_clusters=k, n_init='auto')model.fit(x) # 训练模型# 将当前k值对应的SSE(模型的inertia_属性)添加到列表# SSE是所有样本到其所属聚类中心的距离平方和temp_list.append(model.inertia_)# 绘制肘部法图像 plt.figure() # 创建图形对象 plt.grid() # 添加网格线,便于观察 # 绘制k值(2到99)与对应SSE的关系曲线,红色圆点连线 plt.plot(range(2,100), temp_list[1:], 'or-') # temp_list[1:]跳过k=1的情况 plt.xlabel('k (Number of clusters)') # x轴标签:聚类数量k plt.ylabel('SSE (Sum of Squared Errors)') # y轴标签:误差平方和 plt.title('Elbow Method for Optimal k') # 图表标题 plt.show() # 显示图像 # 肘部法原理:寻找SSE下降速率明显减缓的"拐点",该点对应的k即为较优值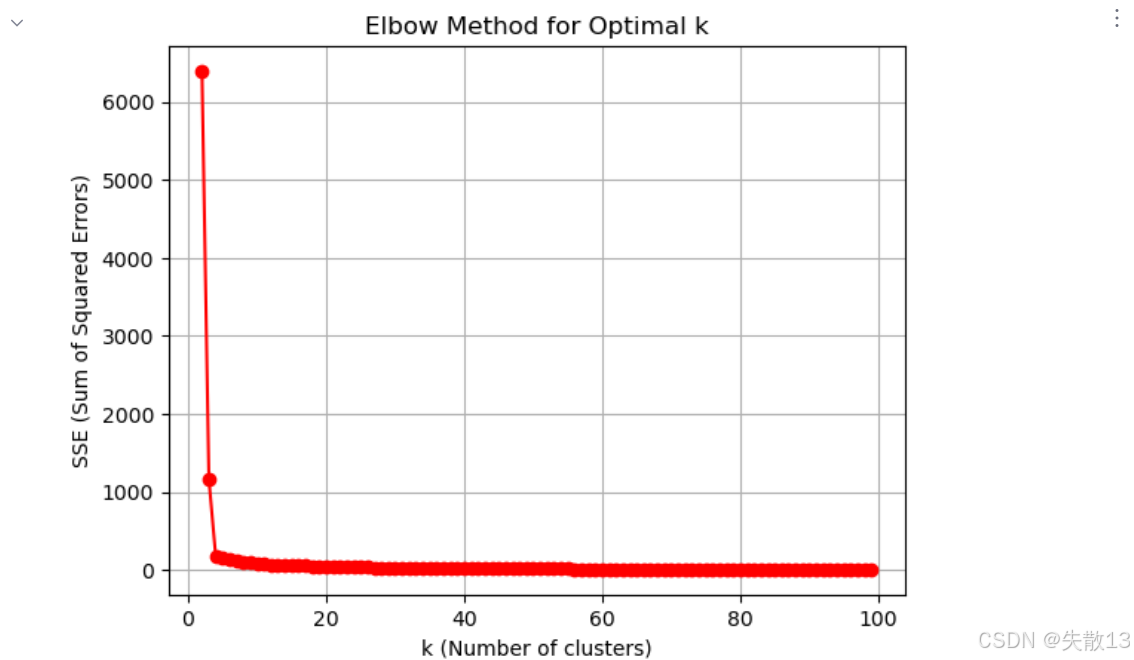
-
使用轮廓系数(Silhouette Coefficient)评估不同k值的聚类效果
# 使用轮廓系数(Silhouette Coefficient)评估不同k值的聚类效果 # 重置存储列表 temp_list = [] # 迭代测试k从2到99的情况(轮廓系数不适用于k=1) for k in range(2,100):model = KMeans(n_clusters=k, n_init='auto') # 创建模型model.fit(x) # 训练模型y_pred = model.predict(x) # 预测聚类标签# 计算轮廓系数并添加到列表,值越接近1表示聚类效果越好temp_list.append(silhouette_score(x, y_pred))# 绘制轮廓系数图像 plt.figure() plt.grid() # 绘制k值与对应轮廓系数的关系曲线 plt.plot(range(2,100), temp_list, 'or-') plt.xlabel('k (Number of clusters)') plt.ylabel('Silhouette Coefficient') # 轮廓系数 plt.title('Silhouette Method for Optimal k') plt.show()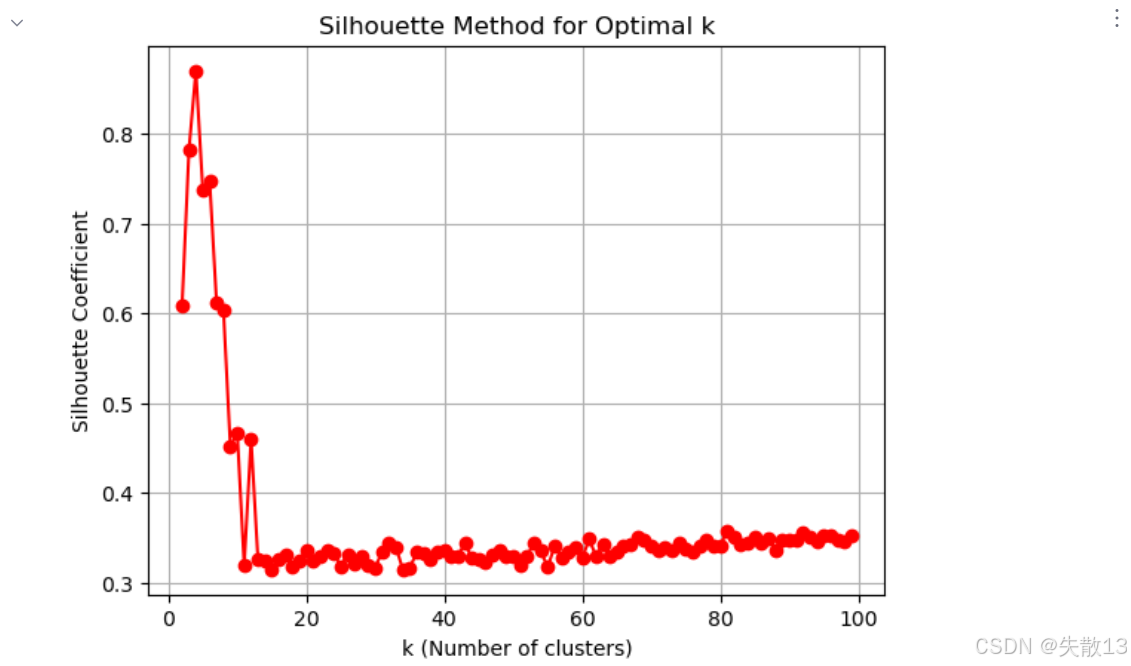
-
使用Calinski-Harabasz指数评估不同k值的聚类效果
# 使用Calinski-Harabasz指数评估不同k值的聚类效果 # 重置存储列表 temp_list = [] # 迭代测试k从2到99的情况 for k in range(2,100):model = KMeans(n_clusters=k, n_init='auto')model.fit(x)y_pred = model.predict(x)# 计算CH指数并添加到列表,值越大表示聚类效果越好temp_list.append(calinski_harabasz_score(x, y_pred))# 绘制CH指数图像 plt.figure() plt.grid() # 绘制k值与对应CH指数的关系曲线 plt.plot(range(2,100), temp_list, 'or-') plt.xlabel('k (Number of clusters)') plt.ylabel('Calinski-Harabasz Score') # CH指数 plt.title('Calinski-Harabasz Method for Optimal k') plt.show()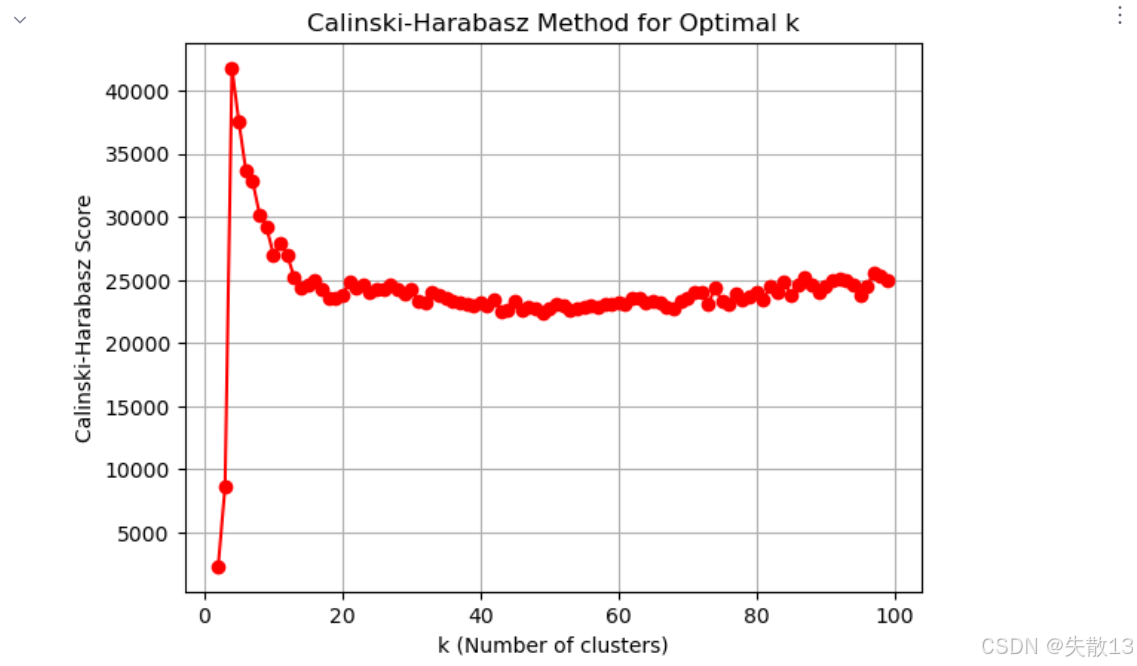
4.5 小结
- 误差平方和SSE:
- 误差平方和的值越小越好
- 主要考量:簇内聚程度
- 肘部法:下降率突然变缓时即认为是最佳的k值
- SC系数:
- 取值为[-1, 1],其值越大越好
- 主要考量:簇内聚程度、簇间分离程度
- CH系数:
- 分数s高则聚类效果越好
- CH达到的目的:用尽量少的类别聚类尽量多的样本,同时获得较好的聚类效果
- 主要考量:簇内聚程度、簇间分离程度、质心个数
5 案例:顾客数据聚类分析
-
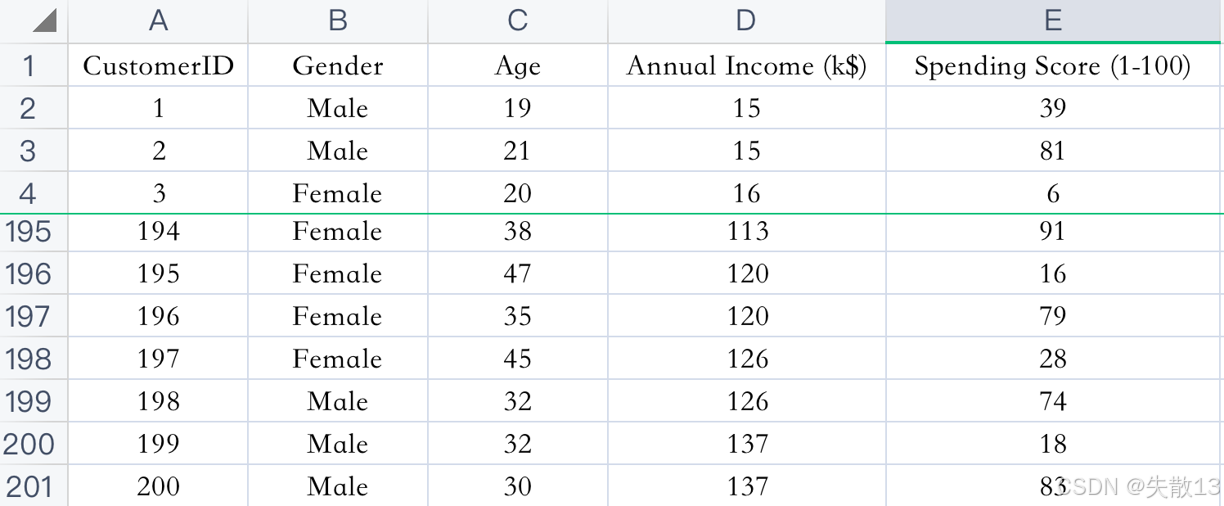
已知:客户性别、年龄、年收入、消费指数
-
需求:对客户进行分析,找到业务突破口,寻找黄金客户
-
导包:
import pandas as pd from sklearn.cluster import KMeans import matplotlib.pyplot as plt plt.rcParams['font.sans-serif'] = ['SimHei'] # 正常显示汉字 plt.rcParams['axes.unicode_minus'] = False # 正常显示负号 from sklearn.metrics import silhouette_score -
加载数据:
# 1.加载数据 data =pd.read_csv('data/customers.csv') print(data.head()) -
特征选择:
# 2.特征选择 # 选择数据中的所有行,第4列和第5列作为聚类特征 x =data.iloc[:,[3,4]] print(x)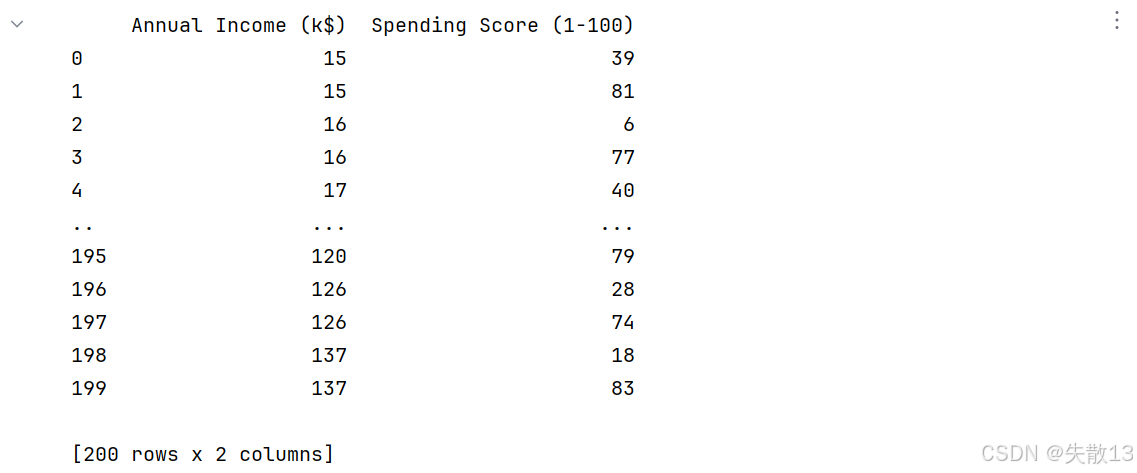
-
模型训练与优化——K值的选择(确定最佳聚类位置)
# 3. 模型训练与优化 # 3.1 K值的选择(确定最佳聚类数量) # 存储不同K值对应的SSE(误差平方和) sse_list = [] # 存储不同K值对应的轮廓系数 sc_list = []# 测试K值从2到19的情况(聚类数通常不会太大,20以内较为常见) for i in range(2, 20):# 创建KMeans模型,设置聚类数为imodel = KMeans(n_clusters=i, n_init='auto') # 添加n_init='auto'避免警告# 使用选择的特征数据训练模型model.fit(x)# 获取当前K值对应的SSE(模型的inertia_属性)sse = model.inertia_sse_list.append(sse)# 预测每个样本的聚类标签y_pred = model.predict(x)# 计算当前K值对应的轮廓系数,评估聚类效果sc_list.append(silhouette_score(x, y_pred)) -
绘制SSE随K值变化的曲线(肘部法)
# 绘制SSE随K值变化的曲线(肘部法) plt.figure(figsize=(10, 6)) plt.grid(True, linestyle='--', alpha=0.7) plt.plot(range(2, 20), sse_list, 'or-', markersize=8, linewidth=2) plt.xlabel('K值(聚类数量)', fontsize=12) plt.ylabel('SSE(误差平方和)', fontsize=12) plt.title('肘部法确定最佳K值', fontsize=14) plt.show()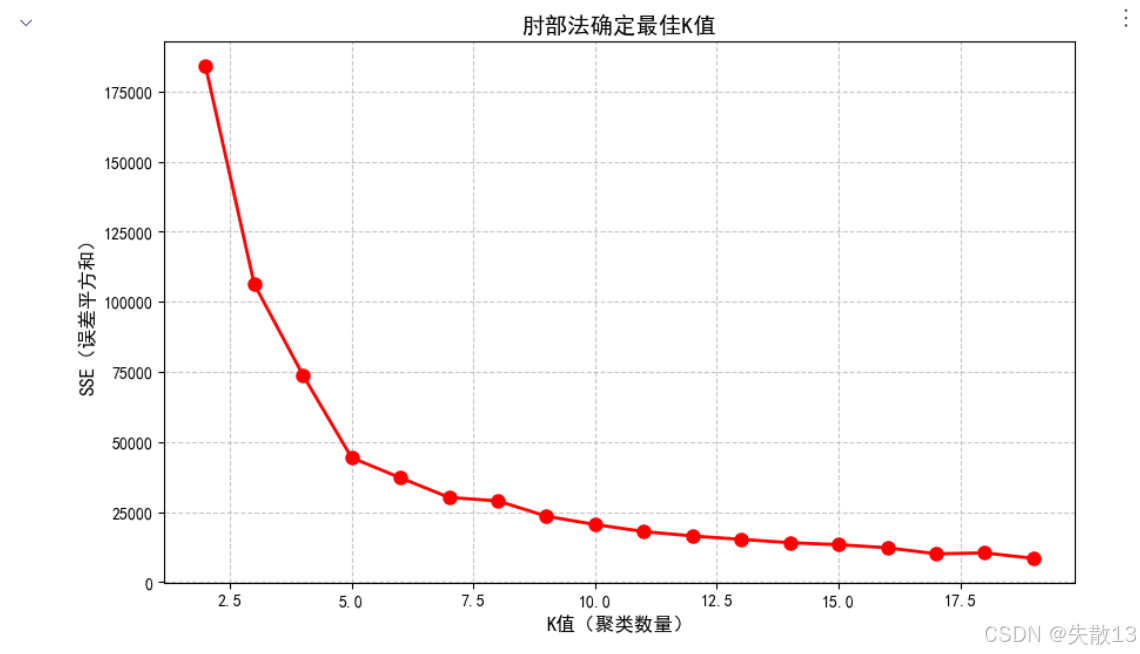
-
绘制轮廓系数随K值变化的曲线
# 绘制轮廓系数随K值变化的曲线 plt.figure(figsize=(10, 6)) plt.grid(True, linestyle='--', alpha=0.7) plt.plot(range(2, 20), sc_list, 'ob-', markersize=8, linewidth=2) plt.xlabel('K值(聚类数量)', fontsize=12) plt.ylabel('轮廓系数', fontsize=12) plt.title('轮廓系数法确定最佳K值', fontsize=14) plt.show()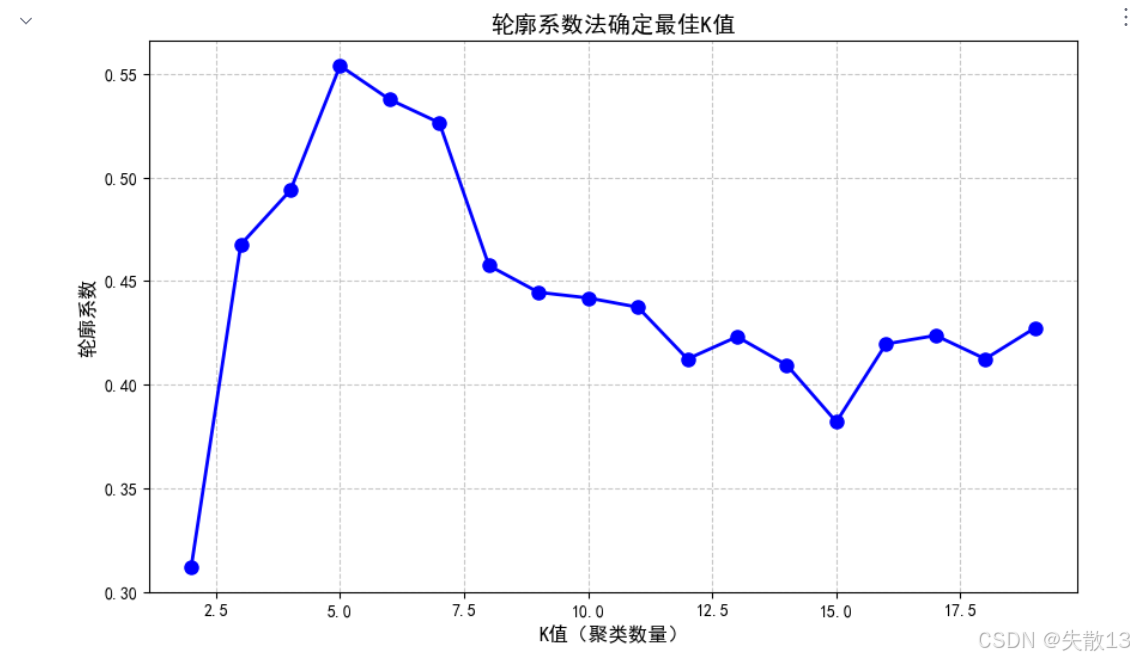
-
根据上述分析结果,选择K=5进行最终聚类
# 3.2 根据上述分析结果,选择K=5进行最终聚类 model = KMeans(n_clusters=5, n_init='auto') # 实例化模型,设置聚类数为5 model.fit(x) # 训练模型 y_pred = model.predict(x) # 预测每个客户的聚类标签 print("聚类结果标签:", y_pred) # 打印聚类标签 print("各聚类中心坐标:\n", model.cluster_centers_) # 打印每个聚类的中心(质心)
-
聚类结果可视化
# 4. 聚类结果可视化 plt.figure(figsize=(10, 8))# 分别绘制每个聚类的散点,使用不同颜色区分 plt.scatter(x.values[y_pred == 0, 0], x.values[y_pred == 0, 1], c='r', label='客户群1', alpha=0.7) plt.scatter(x.values[y_pred == 1, 0], x.values[y_pred == 1, 1], c='b', label='客户群2', alpha=0.7) plt.scatter(x.values[y_pred == 2, 0], x.values[y_pred == 2, 1], c='y', label='客户群3', alpha=0.7) plt.scatter(x.values[y_pred == 3, 0], x.values[y_pred == 3, 1], c='g', label='客户群4', alpha=0.7) plt.scatter(x.values[y_pred == 4, 0], x.values[y_pred == 4, 1], c='gray', label='客户群5', alpha=0.7)# 绘制各聚类的中心(用黑色星号标记) plt.scatter(model.cluster_centers_[:, 0], model.cluster_centers_[:, 1], c='black', s=200, marker='*', label='聚类中心')plt.xlabel('特征1(如:消费金额)', fontsize=12) plt.ylabel('特征2(如:消费频率)', fontsize=12) plt.title('客户分群结果可视化', fontsize=14) plt.legend() # 显示图例 plt.grid(True, linestyle='--', alpha=0.5) plt.show()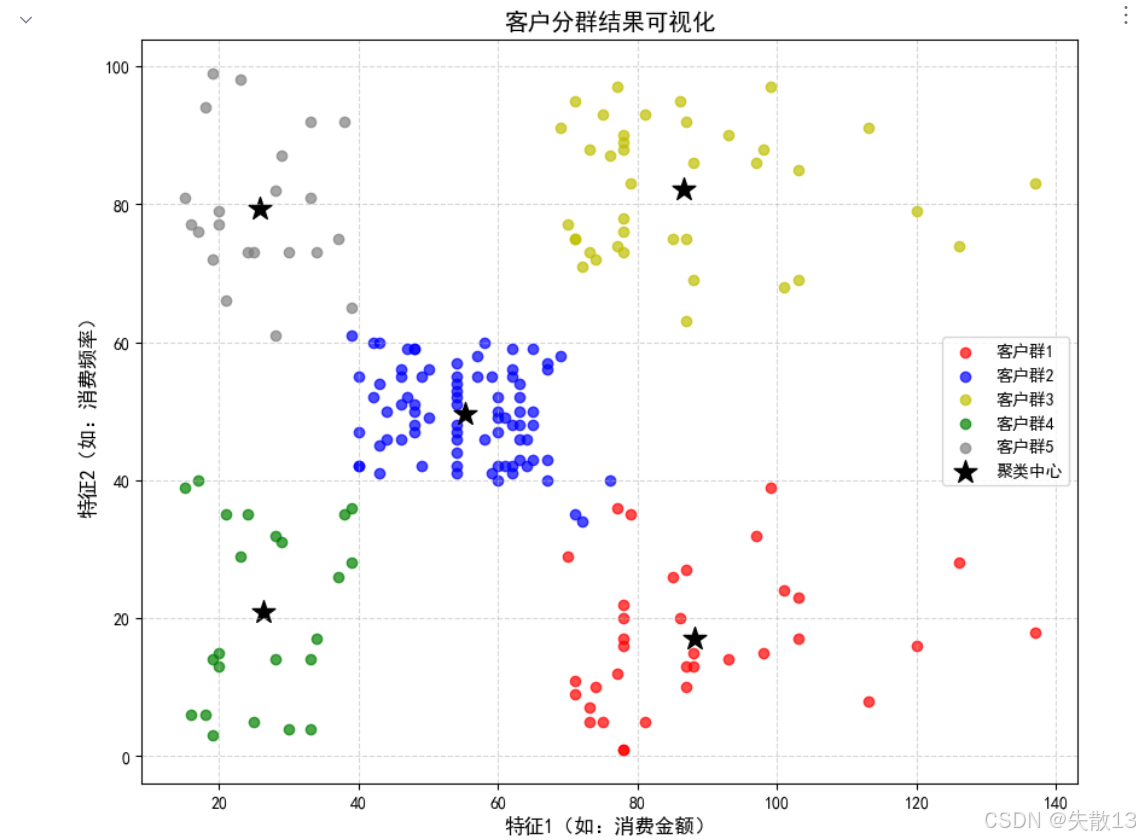



)
)


)



)

)

![[Robotics_py] 路径规划算法 | 启发式函数 | A*算法](http://pic.xiahunao.cn/[Robotics_py] 路径规划算法 | 启发式函数 | A*算法)

 226. 翻转二叉树 (深度优先搜索dfs ))
)
