【1】引言
前序学习进程中,对SVM相关的数学原理进行了探索和推导,相关文章链接包括且不限于:
python学智能算法(二十六)|SVM-拉格朗日函数构造-CSDN博客
python学智能算法(二十八)|SVM-拉格朗日函数求解中-KKT条件_python求解kkt条件-CSDN博客
python学智能算法(三十)|SVM-KKT条件的数学理解_dual svm 的 kkt 条件-CSDN博客
python学智能算法(三十六)|SVM-拉格朗日函数求解(中)-软边界-CSDN博客
在对数学原理进行测试的过程中,必须用到数据集。由于sklearn有成熟的数据集,因此有必要先对sklearn相关的知识点进行学习和掌握,这样才有助于快速理解后面的知识。
【2】线性回归实例解读
官网学习地址:1.1 线性模型-scikit-learn中文社区
线性回归计算的本质非常简单,假设有自变量x=[x1,x2,...,xn] ,因变量$y=[y1,y2}...,yn],线性回归的目的就是找出一组回归系数$w=[w1,w2...,wn]$和偏置量b,使得线性方程成立:
$$y(w,x,b)=\sum_{i=1}^{n}w_{i}\cdot x_{i}+b$$
解读之前,首先给出完整代码:
# 引入绘图模块
import matplotlib.pyplot as plt
# 引入计算模块
import numpy as np
# 引入数据集和线性模块
from sklearn import datasets, linear_model
# 计算均方误差和决定系数
from sklearn.metrics import mean_squared_error, r2_score# Load the diabetes dataset
# 返回二维矩阵diabetes_X,diabetes_X本质是MXN行的矩阵
# 返回一维数组diabetes_y,diabetes_y实际上没有行向量和列向量的区分
diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True)# Use only one feature
# 两个操作,第一个是微数据增加一个新的维度,通过np.newaxis
# 第二个是只提取原本二维矩阵diabetes_X中的第3个特征
# 假如提取原本二维矩阵diabetes_X中的第3个特征是[12,16,18],它们组成了一维数组
# 添加np.newaxis的作用后,获得新的diabetes_X =[[12],[16],[18]]
diabetes_X = diabetes_X[:, np.newaxis, 2]# Split the data into training/testing sets
# 将diabetes_X 除了最后20个数据之外的部分设置为训练数据集的特征,也就是因变量
diabetes_X_train = diabetes_X[:-20]
# 将diabetes_X 最后20个数据设置为测试数据集
diabetes_X_test = diabetes_X[-20:]# Split the targets into training/testing sets
# 将diabetes_y 除了最后20个数据之外的部分设置为训练数据集的特征,也就是因变量
diabetes_y_train = diabetes_y[:-20]
diabetes_y_test = diabetes_y[-20:]# Create linear regression object
# 此处触及线性回归的本质
# regr表面上只是一个变量名
# 但regr存储了linear_model.LinearRegression()可以调用的所有方法和属性
regr = linear_model.LinearRegression()# Train the model using the training sets
# 通过regr可以直接调用linear_model.LinearRegression()类中的fit()方法
# 此处的fit()方法是在diabetes_X_train, diabetes_y_train之间拟合出线性方程
regr.fit(diabetes_X_train, diabetes_y_train)# Make predictions using the testing set
# 将diabetes_X_test代入fit()方法拟合出的线性方程,获得训练出来的因变量
diabetes_y_pred = regr.predict(diabetes_X_test)# The coefficients
# 此处直接输出线性系数,当因变量只有一个,这个数就是直线斜率
print('Coefficients: \n', regr.coef_)
# The mean squared error
# 输出均方误差
print('Mean squared error: %.2f'% mean_squared_error(diabetes_y_test, diabetes_y_pred))
# The coefficient of determination: 1 is perfect prediction
print('Coefficient of determination: %.2f'% r2_score(diabetes_y_test, diabetes_y_pred))# Plot outputs
# 绘制训练值和预测值的对比图
plt.title('test VS predict')
# 训练值,也就是实测值
plt.scatter(diabetes_X_test, diabetes_y_test, color='green',label='test')
# 预测值
plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3,label='predict')
plt.legend()
plt.xticks(())
plt.yticks(())plt.show()【2.1】引入必要模块
# 引入绘图模块
import matplotlib.pyplot as plt
# 引入计算模块
import numpy as np
# 引入数据集和线性模块
from sklearn import datasets, linear_model
# 计算均方误差和决定系数
from sklearn.metrics import mean_squared_error, r2_score这里引入模块是对sklearn的基本操作,每次使用不同的数据集和执行不同的操作,需要引入不同的sklearn子模块。
【2.2】数据处理
数据处理部分将数据集划分为因变量和自变量,再进一步细化为训练集和测试集。
# Load the diabetes dataset
# 返回二维矩阵diabetes_X,diabetes_X本质是MXN行的矩阵
# 返回一维数组diabetes_y,diabetes_y实际上没有行向量和列向量的区分
diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True)# Use only one feature
# 两个操作,第一个是微数据增加一个新的维度,通过np.newaxis
# 第二个是只提取原本二维矩阵diabetes_X中的第3个特征
# 假如提取原本二维矩阵diabetes_X中的第3个特征是[12,16,18],它们组成了一维数组
# 添加np.newaxis的作用后,获得新的diabetes_X =[[12],[16],[18]]
diabetes_X = diabetes_X[:, np.newaxis, 2]# Split the data into training/testing sets
# 将diabetes_X 除了最后20个数据之外的部分设置为训练数据集的特征,也就是因变量
diabetes_X_train = diabetes_X[:-20]
# 将diabetes_X 最后20个数据设置为测试数据集
diabetes_X_test = diabetes_X[-20:]# Split the targets into training/testing sets
# 将diabetes_y 除了最后20个数据之外的部分设置为训练数据集的特征,也就是因变量
diabetes_y_train = diabetes_y[:-20]
diabetes_y_test = diabetes_y[-20:]整个数据处理代码段最核心的目的是实现数据结构划分,适用的最核心代码是return_X_y=True,这一步起到了承上启下的作用,经过这一步数据在结构上分成了自变量组diabetes_X和因变量组diabetes_y,然后取这两组变量的最后20个数据作测试,其余都用于训练。
【2.3】训练和测试
# Create linear regression object
# 此处触及线性回归的本质
# regr表面上只是一个变量名
# 但regr存储了linear_model.LinearRegression()可以调用的所有方法和属性
regr = linear_model.LinearRegression()# Train the model using the training sets
# 通过regr可以直接调用linear_model.LinearRegression()类中的fit()方法
# 此处的fit()方法是在diabetes_X_train, diabetes_y_train之间拟合出线性方程
regr.fit(diabetes_X_train, diabetes_y_train)# Make predictions using the testing set
# 将diabetes_X_test代入fit()方法拟合出的线性方程,获得训练出来的因变量
diabetes_y_pred = regr.predict(diabetes_X_test)# The coefficients
# 此处直接输出线性系数,当因变量只有一个,这个数就是直线斜率
print('Coefficients: \n', regr.coef_)
# The mean squared error
# 输出均方误差
print('Mean squared error: %.2f'% mean_squared_error(diabetes_y_test, diabetes_y_pred))
# The coefficient of determination: 1 is perfect prediction
print('Coefficient of determination: %.2f'% r2_score(diabetes_y_test, diabetes_y_pred))# Plot outputs
# 绘制训练值和预测值的对比图
plt.title('test VS predict')
# 训练值,也就是实测值
plt.scatter(diabetes_X_test, diabetes_y_test, color='green',label='test')
# 预测值
plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3,label='predict')
plt.legend()
plt.xticks(())
plt.yticks(())plt.show()代码运行后的效果为:
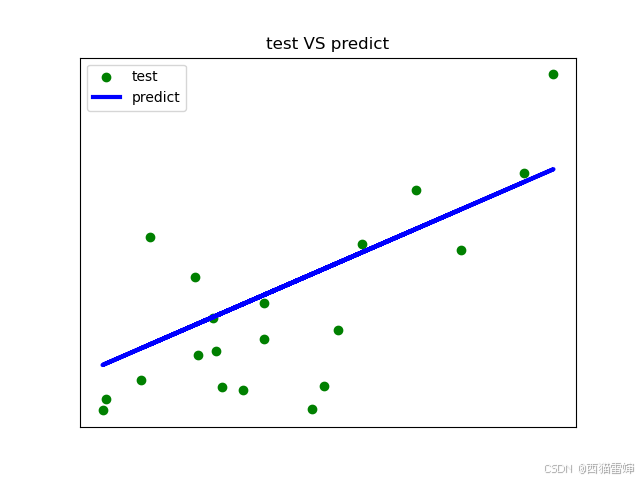
【3】总结
通过构造线性回归实例,初步学习了使用scikitlearn/sklearn模块进行数据处理的技巧。
:AAC编码器)




)



:一文解决 Top K 问题!)









