栈和队列

详细教程可以观看
https://www.bilibili.com/video/BV1nJ411V7bd?spm_id_from=333.788.videopod.episodes&vd_source=daed5b8a51d3ab7eb209efa9d0ff9a34&p=48

栈和队列概念

栈和队列是限定插入和删除只能在表的端点进行的线性表
在这里插入图片描述
在装电池、装弹夹、拿放盘子时都会出现栈的思想，先放入的元素最先出来

在这里插入图片描述
队列时先排队的最先出来——先进先出

栈的定义与特点：

比较维度一般线性表栈
运算规则支持随机存取，可在任意位置插入、删除、读取元素遵循 “后进先出（LIFO）”，操作仅限栈顶（入栈、出栈）
逻辑结构一对一关系一对一关系
存储结构顺序存储（如数组）、链式存储（如链表）等顺序栈、链栈等
适用场景适用于需要灵活操作元素的场景适用于 “后进先出” 逻辑的场景，如函数调用栈、表达式求值
典型操作通过下标直接访问任意位置元素入栈（push）、出栈（pop）、获取栈顶元素（peek）

单向队列的定义与特点：

比较维度单向队列
定义只能在表的一端进行插入运算（尾插），在表的另一端进行删除运算（头删）的线性表
逻辑结构一对一关系
存储结构顺序队或链队，以循环顺序队列更常见
运算规则只能在队首和队尾运算，遵循先进先出（FIFO）原则
实现方式关键掌握入队和出队操作，依顺序队或链队不同而有差异

栈的顺序实现

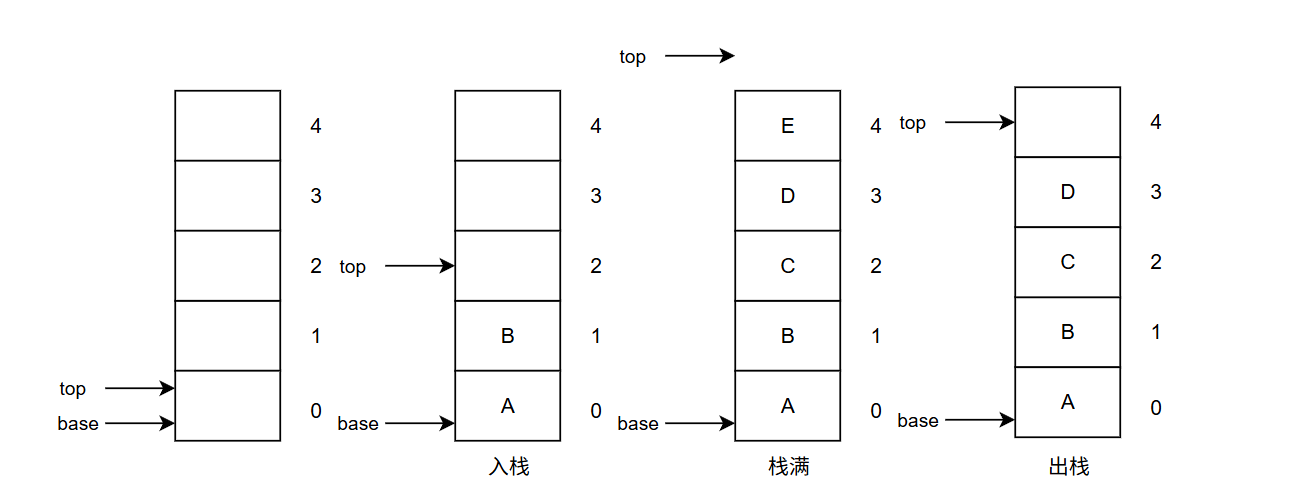
栈的示意图
设置base指针在栈底元素的位置，top表示栈顶元素之上的位置，优点新插入的元素直接在top指针操作即可，计算数量时直接相减，不需要加1。

清空操作：

让top与base指针相等即可。

   // 清空栈void clear() {top = base;       // 重置栈顶指针}

入栈操作：

直接将值复给top指针，然后top后移

   // 入栈操作void push(int value) {*top = value;    // 将值存入栈顶位置top++;           // 栈顶指针上移}

出栈操作：

将top指针前移，然后取值

   // 出栈操作int pop() {top--;           // 栈顶指针下移return *top;     // 返回栈顶元素}

完整代码：
在上边代码加上抛出异常，以及其他一些子功能。

#include <iostream>
#include <stdexcept>
using namespace std;class ArrayStack {
private:int *base;        // 栈底指针（指向数组起始位置）int *top;         // 栈顶指针（指向栈顶元素的下一个位置）int capacity;      // 栈的总容量public:// 构造函数：创建指定容量的栈ArrayStack(int cap) {capacity = cap;base = new int[capacity];top = base;          // 初始时栈顶指针等于栈底指针}// 析构函数：释放动态分配的内存~ArrayStack() {delete[] base;}// 获取栈的容量int getCapacity() {return capacity;}// 获取当前栈中元素数量（通过指针差计算）int size() {return top - base;  // 指针差即为元素数量}// 检查栈是否为空bool isEmpty() {return top == base;}// 检查栈是否已满bool isFull() {return (top - base) == capacity;}// 入栈操作void push(int value) {if (isFull()) {throw overflow_error("栈已满，无法添加元素");}*top = value;    // 将值存入栈顶位置top++;           // 栈顶指针上移}// 出栈操作int pop() {if (isEmpty()) {throw underflow_error("栈为空，无法弹出元素");}top--;           // 栈顶指针下移return *top;     // 返回栈顶元素}// 查看栈顶元素（不弹出）int peek() {if (isEmpty()) {throw underflow_error("栈为空，无法查看栈顶元素");}return *(top - 1); // 返回栈顶元素的值}// 打印栈内容（从栈顶到栈底）void printStack() {if (isEmpty()) {cout << "栈为空" << endl;return;}cout << "栈内容（从顶到底）: ";// 从栈顶向栈底遍历for (int *ptr = top - 1; ptr >= base; ptr--) {cout << *ptr << " ";}cout << endl;}// 清空栈void clear() {top = base;       // 重置栈顶指针}

栈的链表实现

栈的链表实现
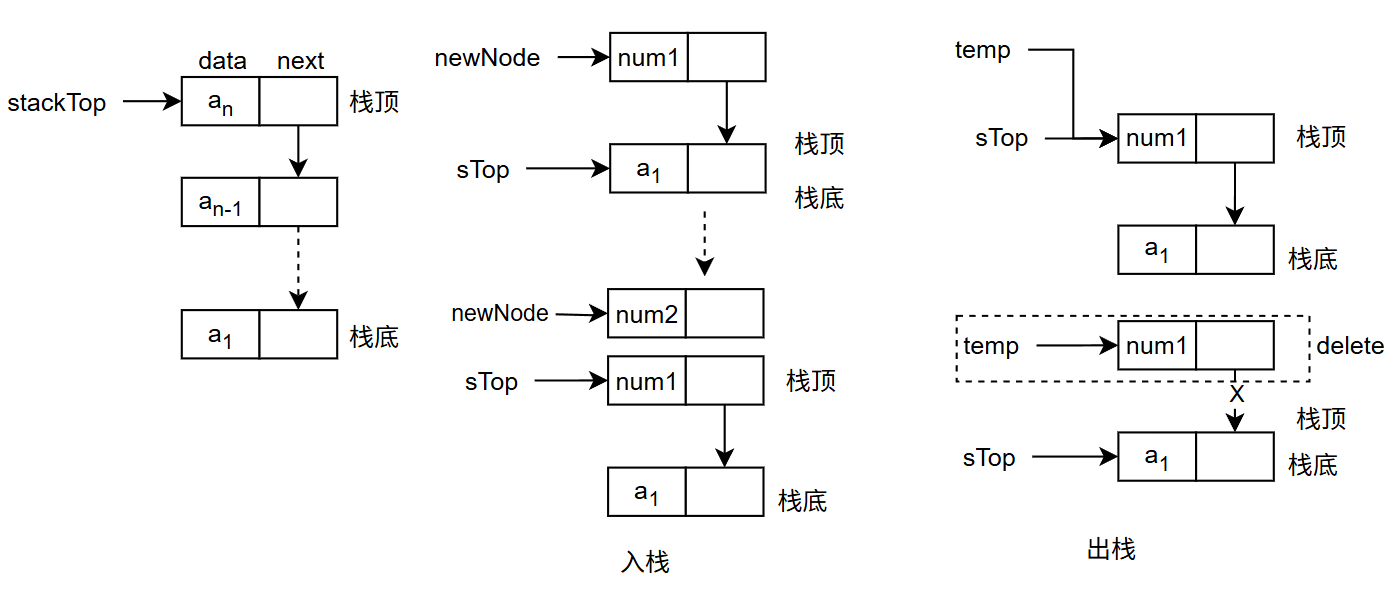
要知道，栈有着后进先出（LIFO）的特性，这就要求新元素入栈（push）和旧元素出栈（pop）都得在栈顶进行操作。

回顾链表的两种插入方法，头插与尾插，在只有一个指针的情况下，采用头插的方法较为简单。原因在于，链表头部进行插入和删除操作的时间复杂度都是 O (1)。要是使用尾插法，在删除尾部节点时，得先遍历到倒数第二个节点，时间复杂度就变成了 O (n)，这显然不符合栈的操作要求。所以这里采用头插法，直接维护一个栈顶头。

完整代码：

// 定义链表节点结构
struct ListNode {int data;ListNode* next;ListNode(int num) : data(num), next(nullptr) {}
};class LinkedListStack {private:ListNode *stackTop; // 将头节点作为栈顶int stkSize;        // 栈的长度public:LinkedListStack() {stackTop = nullptr;stkSize = 0;}~LinkedListStack() {while(stackTop != nullptr) {ListNode* temp = stackTop;stackTop = stackTop->next;delete temp;}   stkSize = 0;}/* 获取栈的长度 */int size() {return stkSize;}/* 判断栈是否为空 */bool isEmpty() {return size() == 0;}/* 入栈 */void push(int num) {ListNode *node = new ListNode(num);node->next = stackTop;stackTop = node;//新结点作为栈顶stkSize++;}/* 出栈 */int pop() {int num = top();ListNode *tmp = stackTop;//创建临时指针指向栈顶stackTop = stackTop->next;//将栈顶指针下移// 释放内存delete tmp;//释放掉要出栈的指针stkSize--;return num;}/* 访问栈顶元素 */int top() {if (isEmpty()){cout<<"栈为空"<<endl;// 考虑返回一个特殊值或抛出异常return -1; }else{return stackTop->data; // 修改：使用正确的成员名}}/* 将 List 转化为 Array 并返回 */vector<int> toVector() {ListNode *node = stackTop;vector<int> res(size());for (int i = res.size() - 1; i >= 0; i--) {res[i] = node->val;node = node->next;}return res;}
};

队列顺序实现

队列表示

回顾单向队列的定义与特点

单向队列的定义与特点：

比较维度单向队列
定义只能在表的一端进行插入运算（尾插），在表的另一端进行删除运算（头删）的线性表
逻辑结构一对一关系
存储结构顺序队或链队，以循环顺序队列更常见
运算规则只能在队首和队尾运算，遵循先进先出（FIFO）原则
实现方式关键掌握入队和出队操作，依顺序队或链队不同而有差异

溢出问题

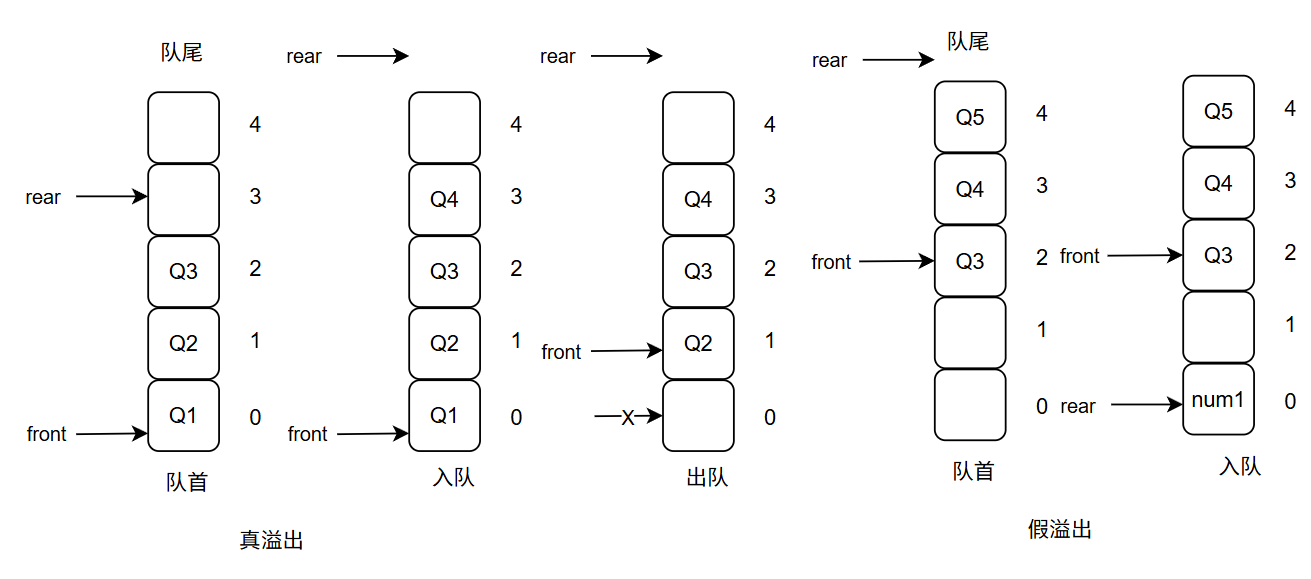
在这里插入图片描述
在入队时随着元素的增加，当尾部指针进行达到最大容量时，发生溢出现象，分为真溢出和假溢出现象：

真溢出： front=0,即首指针从0开始，这时在添加没有位置，对应最左边图

假溢出： 由于front!=0,这是由于进行了出队操作，只能在对头进行删除导致front后移，之前的位置会空下来对应中间和最右边图，这时其实front之前是有空闲位置的。

解决方法：

可以使用首尾相接的环形数组来解决这个问题，让front与rear在越过数组尾部时，直接会搭配数组头部继续遍历，周期性的规律可以使用取余操作来完成，与后边的获取长度，判断是否已经满一起讲解。

以最右边假溢出为例：此时尾指针指向尾元素的后一个位置rear=5==capacity，发生溢出，在添加新的元素时，想让其存储在0所在位置，即rear=1，方法(rear+1)%capacity，(5+1)%5=1

同理删除元素时，front会后移，当front=4，要想在移动到队首0的位置，取余操作(4+1)%5=0,回到最初的位置

求解长度

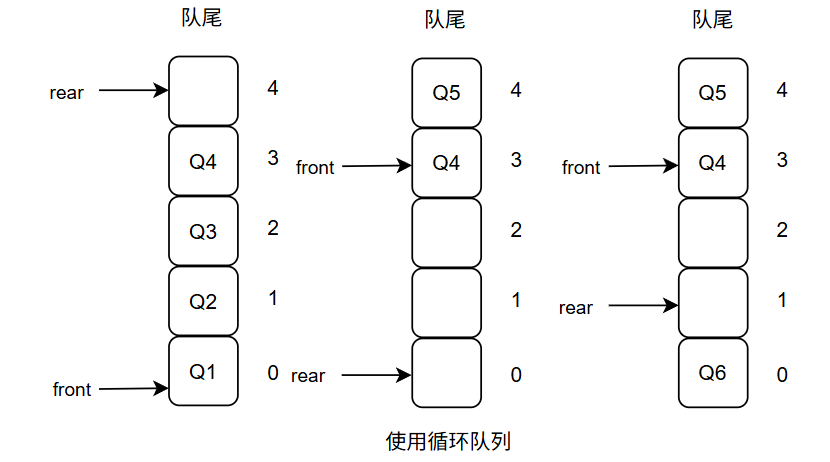
在这里插入图片描述
求解长度的挑战：

rear与front是变化的，与rear、front指针的相对位置有关

公式(rear - front + queCapacity) % queCapacity能够统一处理上述两种情况：

  • 尾指针rear>首指针front，rear指向队尾元素下一个，用rear-front即可，以左边图片为例mod((4-0+5)/5)=4

  • 尾指针rear<首指针front，说明发生了循环队列现象，以中间图片为例，此时front=3,rear=0，用
    mod((0-3+5)/5)=2，等于队列长度

  • 最右边图片mod((1-3+5)/5)=3，等于队列长度；

方法：当假溢出时出现的现象是rear索引以前的元素填充完毕但rear与front之间的元素是空着的 先计算front与rear之间的元素个数，由于rear指向尾元素下一个位置，直接用大数减小数即可，再用总容量减去空着的元素即可得到真实长度。

/* 获取队列的长度 */
int size() {return (rear - front + queCapacity) % queCapacity;
}

判断是否已满

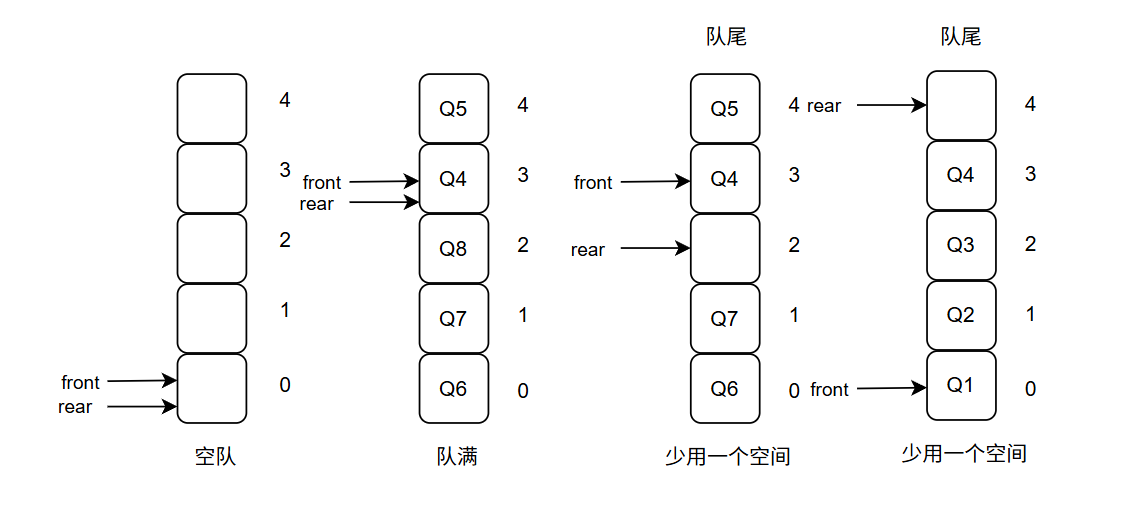
在这里插入图片描述
问题：

在判断队空时方法是判断首尾指针是否相等，因为一般情况即元素并未满的时候，指针不相等，但随着元素的入队会出现首尾指针相等的情况，比如说图中front指向Q4，随着rear指针的移动，rear指向尾元素（图中Q8）的后一个元素，此时就会和front指针相撞，出现首尾指针相等的情况，这种情况下与队空情况相同。

解决方法-少用一个元素空间

如最右边的图所示，rear指向尾元素的下一个位置，此时rear指向空着的元素，如果令rear+1则rear指向和头指针重合，就和队空的情况区别开。同样取余运算是为了解决溢出问题。

/* 判断队列是否已满 */
bool isFull() {return (rear + 1) % queCapacity == front;
}

返回数组

假设环形队列如下：

  • queCapacity = 6（数组下标 0~5）。
  • front = 4，rear = 2（队列有效元素为 4→5→0→1）。
  • 数组nums存储：[7, 8, ?, ?, 5, 6]（?表示无效位置）。

调用toVector()后的结果：

  1. 创建vector，大小为(2-4+6)%6 = 4。
  2. 遍历过程：
    • j=4：arr[0] = nums[4] = 5。
    • j=5：arr[1] = nums[5] = 6。
    • j=0：arr[2] = nums[0] = 7。
    • j=1：arr[3] = nums[1] = 8。
  3. 返回vector：[5, 6, 7, 8]。
/* 将数组转化为 Vector 并返回 */
vector<int> toVector() {//创建数组容器vector<int> arr(size());//遍历环形队列，将非连续转换为连续的for (int i = 0, j = front; j != rear; i++, j = (j + 1) % queCapacity) {arr[i] = nums[j];}return arr;
}

完整代码

class ArrayQueue {private:int *nums;       // 用于存储队列元素的数组int front;       // 队首指针，指向队首元素int rear;        // 队尾指针，指向队尾元素的下一个位置int queCapacity; // 队列容量，含多浪费的空间public:ArrayQueue(int cap) {queCapacity = cap + 1;  // 为用户期望容量添加额外空间nums = new int[queCapacity];front = rear = 0;}~ArrayQueue() {delete[] nums;}/* 获取队列的容量 */int capacity() {return queCapacity-1;}/* 获取队列的长度 */int size() {return (rear - front + queCapacity) % queCapacity;}/* 判断队列是否为空 */bool isEmpty() {return front == rear;}/* 判断队列是否已满 */bool isFull() {return (rear + 1) % queCapacity == front;}/* 入队 */void push(int num) {if (isFull()) {cout << "队列已满" << endl;return;}// 将 num 添加至队尾nums[rear] = num;// 队尾指针向后移动一位，若越过尾部，则返回到数组头部rear = (rear + 1) % queCapacity;}/* 出队 */int pop() {int num = peek();// 队首指针向后移动一位，若越过尾部，则返回到数组头部front = (front + 1) % queCapacity;return num;}/* 访问队首元素 */int peek() {if (isEmpty())throw out_of_range("队列为空");return nums[front];}/* 将数组转化为 Vector 并返回 */vector<int> toVector() {//创建数组容器vector<int> arr(size());//遍历环形队列，将非连续转换为连续的for (int i = 0, j = front; j != rear; i++, j = (j + 1) % queCapacity) {arr[i] = nums[j];}return arr;}
};

队列链表实现

入队

思路：创建一个新节点，链接到尾指针的后继，然后将尾指针指向新节点。

由于未设置头指针，所以在入队时需要判断一个尾指针是否为空，空的话插入的第一个元素既是头结点也是尾节点，否则的话再尾节点添加值即可

  /* 入队 */void push(int num) {ListNode* node = new ListNode(num);if (rear == nullptr) {// 队列为空时，新节点同时作为头尾节点front = node;rear = node;} else {// 队列非空，追加到尾节点后rear->next = node;rear = node;  // 更新尾指针}}

出队

思路：出队只能从头节点开始进行删除，先将头结点进行保存，然后将头指针后移，将头指针删除。

只不过要注意将元素删除的只剩下一个时，头指针与尾指针全都指向最后一个元素。 执行完pop操作，此时头指针后移成为空指针，这时要将尾指针也变为空指针 。

/* 出队 */int pop() {if (isEmpty()) {throw std::out_of_range("队列为空");}ListNode* temp = front;    // 保存待删除节点int num = temp->val;       // 保存返回值front = front->next;       // 头指针后移if (front == nullptr) {rear = nullptr;  // 如果队列变空，重置尾指针}delete temp;         // 删除原头节点return num;}

返回数组

设置一个容器接受这些数据

    /* 将链表转化为 Vector 并返回 */vector<int> toVector() const {vector<int> res;ListNode* current = front;while (current != nullptr) {res.push_back(current->val);current = current->next;}return res;}

完整代码

#include <stdexcept>
#include <vector>// 链表节点定义
struct ListNode {int val;ListNode* next;ListNode(int x) : val(x), next(nullptr) {}
};/* 基于链表实现的队列（无哨兵节点） */
class LinkedListQueue {
private:ListNode* front;  // 头指针（直接指向首元素）ListNode* rear;   // 尾指针（直接指向尾元素）public:LinkedListQueue() : front(nullptr), rear(nullptr) {}  // 初始化空指针~LinkedListQueue() {clear();}// 清空队列void clear() {while (front != nullptr) {ListNode* temp = front;  // 临时节点指向当前头节点front = front->next;     // 头指针后移delete temp;             // 删除原头节点}rear = nullptr;  // 重置尾指针}/* 获取队列的长度 */int size() const {int count = 0;ListNode* current = front;while (current != nullptr) {count++;current = current->next;}return count;}/* 判断队列是否为空 */bool isEmpty() const {return front == nullptr;  // 头指针为空表示队列空}/* 入队 */void push(int num) {ListNode* node = new ListNode(num);if (rear == nullptr) {// 队列为空时，新节点同时作为头尾节点front = node;rear = node;} else {// 队列非空，追加到尾节点后rear->next = node;rear = node;  // 更新尾指针}}/* 出队 */int pop() {if (isEmpty()) {throw std::out_of_range("队列为空");}ListNode* temp = front;    // 保存待删除节点int num = temp->val;       // 保存返回值front = front->next;       // 头指针后移if (front == nullptr) {rear = nullptr;  // 如果队列变空，重置尾指针}delete temp;         // 删除原头节点return num;}/* 访问队首元素 */int peek() const {if (isEmpty()) {throw std::out_of_range("队列为空");}return front->val;  // 直接返回头节点的值}/* 将链表转化为 Vector 并返回 */vector<int> toVector() const {vector<int> res;ListNode* current = front;while (current != nullptr) {res.push_back(current->val);current = current->next;}return res;}
};

双端队列顺序实现

在队列中，我们仅能删除头部元素或在尾部添加元素。双向队列（double-ended queue）提供了更高的灵活性，允许在头部和尾部执行元素的添加或删除操作。

队首入队

让新进来的元素排在先进来之前称为队首入队，先移动后插入

/* 队首入队 */
void pushFront(int num) {if (isFull()) {throw std::overflow_error("Deque is full");}front = (front - 1 + capacity) % capacity;nums[front] = num;
}

可视化示例（容量=5）

初始状态（空队列）：

索引: 0   1   2   3   4[ ] [ ] [ ] [ ] [ ]↑front=0, rear=0

执行 pushFront(10)：

  1. 移动 front：(0 - 1 + 5) % 5 = 4
  2. 在索引4插入10
索引: 0   1   2   3   4[ ] [ ] [ ] [ ] [10]↑front=4 (新队首)

再执行 pushFront(20)：

  1. 移动 front：(4 - 1 + 5) % 5 = 3
  2. 在索引3插入20
索引: 0	1   2   3   4[ ] [ ] [ ] [20] [10]↑          	↑    rear=0      front=3

再执行 pushFront(30)：

  1. 移动 front：(3 - 1 + 5) % 5 = 2
  2. 在索引2插入30
索引: 0   1   2   3   4[ ] [ ] [30] [20] [10]↑       front=2

这样就实现了front始终指向新添加的元素，便于下一次从队首插入。

队尾入队

先进的元素在前，后进的在后，先插入后移动：

/* 队尾入队 */
void pushBack(int num) {if (isFull()) {throw std::overflow_error("Deque is full");}nums[rear] = num;rear = (rear + 1) % capacity;
}

初始状态（空队列）

索引:  0    1    2    3[ ]  [ ]  [ ]  [ ]↑(front=0)↑(rear=0)

操作1: pushBack(10)

  1. 在索引0插入10
  2. rear后移：(0 + 1) % 4 = 1
索引:  0    1    2    3[10] [ ]  [ ]  [ ]↑(front=0)↑(rear=1)

操作2: pushBack(20)

  1. 在索引1插入20
  2. rear后移：(1 + 1) % 4 = 2
索引:  0    1    2    3[10] [20] [ ]  [ ]↑(front=0)↑(rear=2)

操作3: pushBack(30)

  1. 在索引2插入30
  2. rear后移：(2 + 1) % 4 = 3
索引:  0    1    2    3[10] [20] [30] [ ]↑(front=0)↑(rear=3)

队首出队

保留当前队首的值，作为输出，将front后移

/* 队首出队 */int popFront() {if (isEmpty()) {throw std::out_of_range("Deque is empty");}int val = nums[front];front = (front + 1) % capacity;return val;}

队尾出队

先将尾指针前移，返回要出队的元素

 /* 队尾出队 */int popBack() {if (isEmpty()) {throw std::out_of_range("Deque is empty");}rear = (rear - 1 + capacity) % capacity;return nums[rear];}

完整代码

#include <stdexcept>
#include <vector>class ArrayDeque {
private:int* nums;         // 存储队列元素的数组int front;         // 队首指针，指向队首元素int rear;          // 队尾指针，指向队尾元素的下一个位置int capacity;      // 队列总容量（包含额外空间）public:ArrayDeque(int cap) {capacity = cap + 1;  // 多分配一个空间用于区分空和满nums = new int[capacity];front = rear = 0;}~ArrayDeque() {delete[] nums;}/* 获取队列的有效容量（最大元素个数） */int getCapacity() {return capacity - 1;}/* 获取队列的当前长度 */int size() {return (rear - front + capacity) % capacity;}/* 判断队列是否为空 */bool isEmpty() {return front == rear;}/* 判断队列是否已满 */bool isFull() {return (rear + 1) % capacity == front;}/* 队首入队 */void pushFront(int num) {if (isFull()) {throw std::overflow_error("Deque is full");}front = (front - 1 + capacity) % capacity;nums[front] = num;}/* 队尾入队 */void pushBack(int num) {if (isFull()) {throw std::overflow_error("Deque is full");}nums[rear] = num;rear = (rear + 1) % capacity;}/* 队首出队 */int popFront() {if (isEmpty()) {throw std::out_of_range("Deque is empty");}int val = nums[front];front = (front + 1) % capacity;return val;}/* 队尾出队 */int popBack() {if (isEmpty()) {throw std::out_of_range("Deque is empty");}rear = (rear - 1 + capacity) % capacity;return nums[rear];}/* 访问队首元素 */int peekFront() {if (isEmpty()) {throw std::out_of_range("Deque is empty");}return nums[front];}/* 访问队尾元素 */int peekBack() {if (isEmpty()) {throw std::out_of_range("Deque is empty");}int last = (rear - 1 + capacity) % capacity;return nums[last];}/* 将队列转化为 Vector 并返回 */std::vector<int> toVector() {std::vector<int> res(size());for (int i = 0, j = front; j != rear; i++, j = (j + 1) % capacity) {res[i] = nums[j];}return res;}
};

总结

操作指针移动方向元素插入/移除顺序指针移动时机边界处理
队首入队向前先移动指针再插入插入前(front-1+cap)%cap
队尾入队向后先插入再移动指针插入后(rear+1)%cap
队首出队向后先取值再移动指针取值后(front+1)%cap
队尾出队向前先移动指针再取值取值前(rear-1+cap)%cap

双端队列（deque）的实现可以通过不同的方法组合，支持多种元素处理顺序。以下是几种常见的顺序组合方式及其说明：

  • 先进先出（FIFO） - 普通队列模式

组合方式：

​ 入队：使用 pushBack（从队尾添加元素）

​ 出队：使用 popFront（从队首移除元素）

特点：
最先进入队列的元素最先被处理，严格遵循 先进先出 原则，与普通队列（Queue）的行为一致。

  • 后进先出（LIFO） - 栈模式

组合方式：

​ 入栈：使用 pushBack（从队尾添加元素）
​ 出栈：使用 popBack（从队尾移除元素）

特点：
最后进入队列的元素最先被处理，遵循 后进先出 原则，与栈（Stack）的行为一致。

  • 双向操作 - 双端队列模式

组合方式：

​ 队首操作：使用 pushFront（队首插入） + popFront（队首移除）

​ 队尾操作：使用 pushBack（队尾插入） + popBack（队尾移除）

特点：
可以灵活地在队列两端进行插入和删除操作，元素顺序取决于具体调用方式。

区别：

以下两种组合方式都能实现逻辑上的栈：区别在于元素物理存储顺序

操作组合元素物理存储顺序逻辑顺序适用场景
pushBack + popBack最旧元素 → … → 最新元素LIFO传统栈（如函数调用栈）
pushFront + popFront最新元素 → … → 最旧元素LIFO需要队首操作的特殊场景

双端队列链表实现

采用无哨兵结点的方法：
与队列链表实现大致思路相同，只需要补充链接前驱即可。
在队首与队尾出队时其前驱与后继指向空指针即可。

/* 双向链表节点 */
struct DoublyListNode {int val;              // 节点值DoublyListNode *next; // 后继节点指针DoublyListNode *prev; // 前驱节点指针DoublyListNode(int val) : val(val), prev(nullptr), next(nullptr) {}
};/* 基于双向链表实现的双向队列 */
class LinkedListDeque {private:DoublyListNode *front, *rear; // 头节点 front ，尾节点 rearint queSize = 0;              // 双向队列的长度public:/* 构造方法 */LinkedListDeque() : front(nullptr), rear(nullptr) {}/* 析构方法 */~LinkedListDeque() {// 遍历链表删除节点，释放内存DoublyListNode *pre, *cur = front;while (cur != nullptr) {pre = cur;cur = cur->next;delete pre;}}/* 获取双向队列的长度 */int size() {return queSize;}/* 判断双向队列是否为空 */bool isEmpty() {return size() == 0;}/* 队首入队 */void pushFirst(int num) {DoublyListNode* node = new DoublyListNode(num);if (isEmpty()) {front = rear = node;} else {node->next = front;front->prev = node;front = node;}queSize++;}/* 队尾入队 */void pushLast(int num) {DoublyListNode* node = new DoublyListNode(num);if (isEmpty()) {front = rear = node;} else {rear->next = node;node->prev = rear;rear = node;}queSize++;}/* 队首出队 */int popFirst() {if (isEmpty()) throw out_of_range("队列为空");int val = front->val;DoublyListNode* temp = front;front = front->next;if (front != nullptr) {front->prev = nullptr;} else {rear = nullptr; // 若队列已空，更新 rear}delete temp;queSize--;return val;}/* 队尾出队 */int popLast() {if (isEmpty()) throw out_of_range("队列为空");int val = rear->val;DoublyListNode* temp = rear;rear = rear->prev;if (rear != nullptr) {rear->next = nullptr;} else {front = nullptr; // 若队列已空，更新 front}delete temp;queSize--;return val;}/* 返回数组用于打印 */vector<int> toVector() {DoublyListNode *node = front;vector<int> res(size());for (int i = 0; i < res.size(); i++) {res[i] = node->val;node = node->next;}return res;}
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若转载，请注明出处：http://www.pswp.cn/diannao/93295.shtml
繁体地址，请注明出处：http://hk.pswp.cn/diannao/93295.shtml
英文地址，请注明出处：http://en.pswp.cn/diannao/93295.shtml

如若内容造成侵权/违法违规/事实不符，请联系英文站点网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

net8.0一键创建支持(Redis)

net8.0一键创建支持(Redis)

Necore项目生成器 - 在线创建Necore模板项目 | 一键下载 RedisController.cs using CSRedis; using Microsoft.AspNetCore.Http; using Microsoft.AspNetCore.Mvc; using UnT.Template.Application.Responses; using UnT.Template.Domain;namespace UnT.Template.Controllers {…
阅读更多...
Leetcode——42. 接雨水

Leetcode——42. 接雨水

还记得第一次见该题根本无从下手。其实&#xff0c;我们不妨把问题拆解&#xff0c;简单化。不要怕自己写的是暴力算法&#xff0c;有很多算法技巧其实就是在暴力算法的基础上优化得来。题目目的是求所有可接雨水数量&#xff0c;我们可以求出每一个位置可接雨水数量&#xff0…
阅读更多...
Go 语言--＞指针

Go 语言--＞指针

Go 语言–>指针 它允许你操作内存中的实际数据&#xff0c;而不仅仅是数据的副本。指针存储的是另一个变量的内存地址&#xff0c;而不是变量的实际值。 1. 什么是指针 指针是存储变量内存地址的变量&#xff0c;它指向另一个变量。通过指针&#xff0c;你可以间接地访问和修…
阅读更多...
软工八将：软件开发全流程核心角色体系解析

软工八将：软件开发全流程核心角色体系解析

软工八将&#xff1a;软件开发全流程核心角色体系解析 作者注&#xff1a;本概念是由大学生董翔提出&#xff0c;具有一些影响意义。 在现代软件开发领域&#xff0c;团队角色的专业化分工是产品成功的核心保障。“软工八将”作为一套系统梳理软件开发全流程核心角色的术语&…
阅读更多...
安全风险监测系统是什么？内容有哪些？

安全风险监测系统是什么？内容有哪些？

安全风险监测系统是基于物联网感知网络与智能分析技术的综合管理平台&#xff0c;通过实时采集、分析和评估各类安全风险指标&#xff0c;构建起覆盖识别、预警、处置全流程的主动防御体系。作为现代安全管理的中枢神经系统&#xff0c;该系统实现了从被动响应到主动预防的范式…
阅读更多...
车载诊断架构 ---面向售后的DTC应该怎么样填写？

车载诊断架构 ---面向售后的DTC应该怎么样填写？

我是穿拖鞋的汉子，魔都中坚持长期主义的汽车电子工程师。 老规矩，分享一段喜欢的文字，避免自己成为高知识低文化的工程师： 简单，单纯，喜欢独处，独来独往，不易合同频过着接地气的生活，除了生存温饱问题之外，没有什么过多的欲望，表面看起来很高冷，内心热情，如果你身…
阅读更多...
墨者：SQL注入漏洞测试(宽字节)

墨者：SQL注入漏洞测试(宽字节)

墨者学院&#xff1a;SQL注入漏洞测试(宽字节)&#x1f680; 1. 宽字节注入原理✨ 1.1. 与普通注入对比⭐ 特性普通注入宽字节注入适用场景无转义处理使用addslashes()等转义函数核心原理直接闭合引号利用GBK等编码吞掉转义符\关键字符 " -- #%df %5c防御难度易防御需调…
阅读更多...
（二）Eshop（RabbitMQ手动）

（二）Eshop（RabbitMQ手动）

文章目录项目地址一、Rabbit MQ1.1 Pulibsher1. IRabbitMQPublisher接口2. RabbitMQPublisher接口实现3. 使用1.2 Consumer1. 消费接口2. 实现消费者接口项目地址 教程作者&#xff1a;教程地址&#xff1a; 代码仓库地址&#xff1a; 所用到的框架和插件&#xff1a; dbt a…
阅读更多...
WPF高级学习（一）

WPF高级学习（一）

文章目录一、理解进程和线程1. 进程&#xff1a;就像一个独立的“工厂”举例&#xff1a;2. 线程&#xff1a;就像工厂里的“工人”举例&#xff1a;总结&#xff1a;进程 vs 线程二、线程一、WPF 中的线程类型二、核心规则&#xff1a;线程亲和性&#xff08;Thread Affinity&…
阅读更多...
JAVA知识点（四）：SpringBoot与分布式、微服务架构

JAVA知识点（四）：SpringBoot与分布式、微服务架构

文章目录SpringBoot 使用 Validation 进行参数校验并统一返回校验异常引入相应的依赖Validation的基本校验注解添加参数校验在DTO的属性上添加校验在controller对应的DTO添加Valid或者Validated对于复杂String校验我们可以使用正则来校验&#xff0c;如下所示&#xff1a;自定义…
阅读更多...
GPU 服务器ecc报错处理

GPU 服务器ecc报错处理

1. 常见原因分析内存硬件问题&#xff1a;DIMM 内存模块损坏或接触不良&#xff08;最常见原因&#xff09;。内存插槽氧化、松动或物理损坏。内存与主板兼容性问题&#xff08;尤其是非原厂内存&#xff09;。环境因素&#xff1a;服务器内部温度过高&#xff0c;导致内存稳定…
阅读更多...
STM32入门之通用定时器PWM

STM32入门之通用定时器PWM

一、通用定时器简介STM32通用定时器由一个通过可编程预分频器驱动的16位自动重装载计数器组成&#xff0c;适用于多种应用场景&#xff0c;包括测量输入信号的脉冲长度&#xff08;利用输入捕获功能&#xff09;和生成输出波形&#xff08;使用输出比较及PWM功能&#xff09;。…
阅读更多...
第十八节 MATLAB for循环

第十八节 MATLAB for循环

MATLAB中 for 循环是一个重复的控制结构&#xff0c;可以有效地写一个循环&#xff0c;只是执行的次数是特定的。MATLAB for 循环语法:MATLAB中的 for循环的语法如下&#xff1a;for index values<program statements>... endfor 循环的值有下述三种形式之一&#xff1a…
阅读更多...
嵌入式硬件篇---zigbee无线串口通信问题解决方法

嵌入式硬件篇---zigbee无线串口通信问题解决方法

针对 ZigBee 无线串口通信中接收异常的问题&#xff0c;需结合其射频特性、网络机制、硬件配置等多维度原因&#xff0c;采取针对性解决措施。以下从具体场景出发&#xff0c;提供可落地的解决方法&#xff1a;一、解决射频层干扰与信号衰减问题射频层是无线通信的基础&#xf…
阅读更多...
移动高清盒子6PRO-河南创维E900V22D-晶晨S905L3B-4+16G-安卓9-线刷固件包

移动高清盒子6PRO-河南创维E900V22D-晶晨S905L3B-4+16G-安卓9-线刷固件包

移动高清盒子6PRO-河南创维E900V22D-晶晨S905L3B-416G-安卓9-线刷固件包线刷方法&#xff1a;1、准备好一根双公头USB线刷刷机线&#xff0c;长度30-50CM长度最佳&#xff0c;同时准备一台电脑&#xff1b;2、电脑上安装好刷机工具Amlogic USB Burning Tool 软件 →打开软件 →…
阅读更多...
台式电脑有多个风扇开机只有部分转动的原因

台式电脑有多个风扇开机只有部分转动的原因

一、风扇未连接或连接松动这是最常见的原因之一&#xff0c;台式机风扇通常需要通过线材与主板或电源连接&#xff1a;主板接口问题&#xff1a;CPU 风扇、机箱风扇等多连接到主板的风扇接口&#xff08;如 CPU_FAN、SYS_FAN&#xff09;&#xff0c;若线材未插紧、插错接口&am…
阅读更多...
【测试报告】思绪网（Java+Selenium+Jmeter自动化测试）

【测试报告】思绪网（Java+Selenium+Jmeter自动化测试）

一、项目简介思绪网作为一种在线交流平台&#xff0c;支持用户在平台下发布文章&#xff0c;并进行讨论。主要由登录页面&#xff0c;论坛页面&#xff0c;帖子编辑页&#xff0c;帖子详情页等页面组成。二、项目功能1.登录页面&#xff1a;输入正确的账号密码进行登录,跳转博客…
阅读更多...
Nestjs框架: 基于Mongodb的多租户功能集成和优化

Nestjs框架: 基于Mongodb的多租户功能集成和优化

概述 基于前文&#xff0c;我们知道如何集成多租户的相关功能了, 现在我们继续集成Monodb的多租户形式需要注意的是&#xff0c;MongoDB 在 NestJS 中的使用过程中存在一些“坑点”如果按照默认方式集成&#xff0c;会发现连接数在不断增长&#xff0c;即使我们请求的是相同的数…
阅读更多...
如何利用机器学习分析筛选生物标记物

如何利用机器学习分析筛选生物标记物

在生物信息学中&#xff0c;Lasso回归、随机森林&#xff08;Random Forest&#xff09;和XGBoost因其各自的特性和优势&#xff0c;被广泛应用于基因组学、蛋白质组学、药物发现和疾病机制研究等领域。 Lasso回归 癌症亚型分类&#xff1a;从TCGA数据中筛选驱动基因&#xf…
阅读更多...
计算机网络（基础篇）

计算机网络（基础篇）

TCP/IP 网络模型 应用层&#xff08;Application Layer&#xff09; 应用层只需要专注于为用户提供应用功能&#xff0c;比如 HTTP、FTP、Telnet、DNS、SMTP等。应用层是工作在操作系统中的用户态&#xff0c;传输层及以下则工作在内核态。传输层&#xff08;Transport Layer&a…
阅读更多...
最新文章

Copyright @ 2022~2023