目录
一、图像噪点消除噪声:
1、概念
2、均值滤波
3、方框滤波
4 、高斯滤波
5、中值滤波
6、双边滤波
7、总结
一、图像噪点消除噪声:
1、概念
指图像中的一些干扰因素,通常是由图像采集设备、传输信道等因素造成的,表现为图像中随机的亮度,也可以理解为有那么一些点的像素值与周围的像素值格格不入。常见的噪声类型包括高斯噪声和椒盐噪声。高斯噪声是一种分布符合正态分布的噪声,会使图像变得模糊或有噪点。椒盐噪声则是一些黑白色的像素值分布在原图像中
滤波器:也可以叫做卷积核,与自适应二值化中的核一样,本身是一个小的区域,有着特定的核值,并且工作原理也是在原图上进行滑动并计算中心像素点的像素值。滤波器可分为线性滤波和非线性滤波,线性滤波对邻域中的像素进行线性运算,如在核的范围内进行加权求和,常见的线性滤波器有均值滤波、方框滤波、高斯滤波等。非线性滤波则是利用原始图像与模板之间的一种逻辑关系得到结果,常见的非线性滤波器中有中值滤波器、双边滤波器等
滤波与模糊联系与区别:
它们都属于卷积,不同滤波方法之间只是卷积核不同(对线性滤波而言)
低通滤波器是模糊,高通滤波器是锐化
低通滤波器就是允许低频信号通过,在图像中边缘和噪点都相当于高频部分,所以低通滤波 器用于去除噪点、平滑和模糊图像。高通滤波器则反之,用来增强图像边缘,进行锐化处理。
(注意:椒盐噪声可以理解为斑点,随机出现在图像中的黑点或白点;高斯噪声可以理解为拍摄图片时由于光照等原因造成的噪声)
2、均值滤波
均值滤波是一种最简单的滤波处理,它取的是卷积核区域内元素的均值,3×3的滤波核如下:
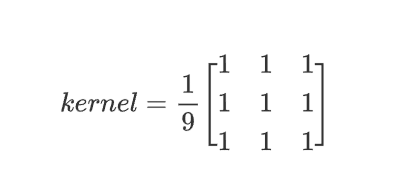

3、方框滤波
方框滤波跟均值滤波很像,如3×3的滤波核如下:
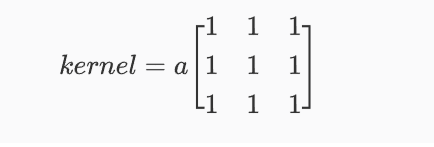
cv2.boxFilter(img, ddepth, ksize, normalize)ddepth:输出图像的深度,-1代表使用原图像的深度
图像深度是指在数字图像处理和计算机视觉领域中,每个像素点所使用的位数,图像深度决 定了图像能够表达的颜色数量或灰度级
ksize:代表卷积核的大小,(ksize=3,则代表使用3×3的卷积核)
normalize:当normalize为True的时候,方框滤波就是均值滤波,上式中的a就等于1/9; normalize为False的时候,a=1,相当于求区域内的像素和

(其滤波的过程与均值滤波一模一样,都采用卷积核从图像左上角开始,逐个计算对应位置的像素值,并从左至右、从上至下滑动卷积核,直至到达图像右下角,唯一的区别就是核值可能会不同 )
4 、高斯滤波
高斯滤波是一种常用的图像处理技术,主要用于平滑图像、去除噪声。它通过使用高斯函数(正态分布)作为卷积核来对图像进行模糊处理
前面两种滤波方式,卷积核内的每个值都一样,也就是说图像区域中每个像素的权重也就一样。高斯滤波的卷积核权重并不相同:中间像素点权重最高,越远离中心的像素权重越小
我们还是以3*3的卷积核为例,其核值如下所示:

得到了卷积核的核值之后,其滤波过程与上面两种滤波方式的滤波过程一样,都是用卷积核从图像左上角开始,逐个计算对应位置的像素值,并从左至右、从上至下滑动卷积核,直至到达图像右下角,唯一的区别就是核值不同
cv2.GaussianBlur(img, ksize, sigmaX)ksize:代表卷积核的大小,(ksize=3,则代表使用3×3的卷积核
sigmaX:就是高斯函数里的值,σx值越大,模糊效果越明显。高斯滤波相比均值滤波效率要慢,但可以有效消除高斯噪声,能保留更多的图像细节,所以经常被称为最有用的滤波器

5、中值滤波
中值又叫中位数,是所有数排序后取中间的值。中值滤波没有核值,而是在原图中从左上角开始,将卷积核区域内的像素值进行排序,并选取中值作为卷积核的中点的像素值
中值滤波就是用区域内的中值来代替本像素值,所以那种孤立的斑点,如0或255很容易消除掉,适用于去除椒盐噪声和斑点噪声。中值是一种非线性操作,效率相比前面几种线性滤波要慢

6、双边滤波
模糊操作基本都会损失掉图像细节信息,尤其前面介绍的线性滤波器,图像的边缘信息很难保留下来。然而,边缘(edge)信息是图像中很重要的一个特征,所以这才有了双边滤波
双边滤波的基本思路是同时考虑将要被滤波的像素点的空域信息(周围像素点的位置的权重)和值域信息(周围像素点的像素值的权重)。为什么要添加值域信息呢?是因为假设图像在空间中是缓慢变化的话,那么临近的像素点会更相近,但是这个假设在图像的边缘处会不成立,因为图像的边缘处的像素点必不会相近。因此在边缘处如果只是使用空域信息来进行滤波的话,得到的结果必然是边缘被模糊了,这样我们就丢掉了边缘信息,因此添加了值域信息。
双边滤波采用了两个高斯滤波的结合,一个负责计算空间邻近度的权值(也就是空域信息),也就是上面的高斯滤波器,另一个负责计算像素值相似度的权值(也就是值域信息),也是一个高斯滤波器
cv2.bilateralFilter(src, d, sigmaColor, sigmaSpace)d:过滤时周围每个像素领域的直径
sigmaColor:在color space(色彩空间)中过滤sigma。参数越大,那些颜色足够相近的的颜色的影响越大。较大的sigmaColor值意味着更大的颜色差异将被允许参与到加权平均中,从而使得颜色相近但不完全相同的像素也能够相互影响
sigmaSpace:在coordinate space(坐标空间)中过滤sigma。这个参数是坐标空间中的标准差,决定了像素位置对滤波结果的影响程度。它定义了在图像的空间域中,一个像素可以影响周围像素的最大距离
关于2个sigma参数:
简单起见,可以令2个sigma的值相等;
如果他们很小(小于10),那么滤波器几乎没有什么效果;
如果他们很大(大于150),那么滤波器的效果会很强,使图像显得非常卡通化。
关于参数d:
过大的滤波器(d>5)执行效率低。
对于实时应用,建议取d=5;
对于需要过滤严重噪声的离线应用,可取d=9;
7、总结
在不知道用什么滤波器好的时候,优先高斯滤波,然后均值滤波。
斑点和椒盐噪声优先使用中值滤波。
要去除噪点的同时尽可能保留更多的边缘信息,使用双边滤波。
线性滤波方式:均值滤波、方框滤波、高斯滤波(速度相对快)。
非线性滤波方式:中值滤波、双边滤波(速度相对慢)。


)



通讯--tcp客户端)

)



)

)
)



