概率密度函数（PDF）与概率质量函数（PMF）说明

基本概念区分

对于连续型随机变量，通常使用 概率密度函数 (Probability Density Function, PDF) 进行描述；这与离散型随机变量使用的 概率质量函数 (Probability Mass Function, PMF) 有本质区别。

• PMF：可以直接代入变量值求得对应事件的概率
• PDF：代入变量值后得到的是 概率密度值，而非概率本身

连续型随机变量的概率特性

1. 单点概率为零
   对于任意实数 $x$，$P(X=x)=0$

2. 区间概率计算
   连续型变量的概率必须通过积分计算：
   $$P(a\le X\le b)={\int }_a^{b}f(x)dx$$

3. 概率密度的物理意义
   PDF 在某点的取值反映该区域概率的 “密集程度”，其值的大小与概率成正比关系

PDF 的基本性质

1. 非负性
   $$f(x)\ge 0\forall x\in \mathbb{R}$$

2. 归一性
   $${\int }_{-\infty }^{+\infty }f(x)dx=1$$

概率质量函数(PDF)和累积分布函数(CDF)

互逆关系

• 从 PDF 到 CDF：
  $$F(x)={\int }_{-\infty }^{x}f(t)dt$$

• 从 CDF 到 PDF：
  $$f(x)=\frac{d}{dx}F(x)$$

概率计算的等价性

对于任意区间 $[a,b]$，概率可表示为：很多情况计算概率时,分布函数使用起来会更简单一些(避免积分运算);
$$\boxed{P(a<X\le b)=F(b)-F(a)={\int }_a^{b}f(x)dx}$$

均匀分布

应用场景实例

1.在java中使用new Random().nextDouble(),生成一个$[0,1]$之间的双精度浮点型伪随机数,数据出现在任意一个区间的可能性是相同的,换言之生成的随机数,均匀的散布在$[0,1]$之间;
2.某公交车每30分钟固定发车一次，乘客在任意时刻到达车站。那么乘客的候车时间在$[0,30]$分钟之间,并且等候任意分钟($[0,30]$)是等可能的;

定义

连续均匀分布（Uniform Distribution）的核心特征是概率密度在整个区间内恒定,即等可能性,是最简单的连续型概率分布之一。
记法:
$$\boxed{X\sim U(a,b)或X\sim \text{Uniform}(a,b)}$$
读作:$X$服从参数为$a,b$的连续均匀分布;

则例1记为:$X\sim U(0,1)$
例2记为:$X\sim U(0,30)$

随机变量

连续型随机变量$X$，其取值范围限定在某个有限区间 $[a,b]$内，且在该区间内每个实数的取值概率密度相等。换句话说，$X$ 是取值在区间 $[a,b]$上均匀分布的随机数。

• 例1定义$X,X\in [0,1]$是生成的随机数的值;
• 例2定义$X,X\in [0,30]$为乘客的等候时间;

参数

连续均匀分布的参数有2个,即左右区间值$a,b$;随机变量取值在这个区间内的概率是1;

函数表达

由定义可得

1. 在整个定义区间$[a,b]$上,概率均匀分布,即任意一个子集,若区间长度则概率相等.则概率相同
2. $P(a\le X\le b)=1$

由于概率是均匀的,则累积分布函数$F(X)$应该是线性的,并且$F(a)=0,F(b)=1$;
设$F(x)=kx+C$,并且有:
$$\{\begin{array}{l}F(a)=0\\ F(b)=1\end{array}$$
解得
$$F(x)=\frac{1}{b-a}x-\frac{a}{b-a}$$
即
$$\boxed{F(x)=\frac{x-a}{b-a}}$$
故概率密度函数$f(x)=F^{\prime }(x)$
$$\boxed{f(x)=\{\begin{array}{l}\frac{1}{b-a},a\le X\le b\\ 0,其他\end{array}}$$
即,求$X$在$[m,n]$区间上的概率即:
$$\boxed{P(m\le X\le n)={\int }_m^n\frac{1}{b-a}dx=\frac{n-m}{b-a},a\le m\le n\le b}$$

分布特征值

• 期望,很好理解就是定于区间的juzn
  $$E(X)=\frac{a+b}{2}$$
• 方差$$\text{Var}(X)=\frac{(b-a{)}^2}{12}$$

推导:
对于连续型随机变量 $X$，其概率密度函数为 $f(x)$，期望 $E(x)$定义为:
$$\begin{array}{rl}E(X)& ={\int }_{-\infty }^{+\infty }x\cdot f(x)dx\end{array}$$
对于服从均匀分布的随机变量$X\sim U(a,b)$则有:
$$\begin{array}{rl}E(X)& ={\int }_b^{a}x\cdot \frac{1}{b-a}dx\\ & =\frac{1}{b-a}{\int }_b^{a}xdx\\ & =\frac{1}{b-a}\times {\left[\frac{x^2}{2}\right]}_a^b\\ & =\frac{1}{b-a}\times \frac{b^2-a^2}{2}\\ & =\frac{a+b}{2}\end{array}$$

方差 $\text{Var}(X)$定义为:
$$\text{Var}(X)=E(X^2)-[E(X){]}^2$$
对于服从均匀分布的随机变量$X\sim U(a,b)$则有:
$$\begin{array}{rl}E(X^2)& ={\int }_b^a{x}^2\cdot \frac{1}{b-a}dx\\ & =\frac{1}{b-a}{\int }_b^a{x}^{2}dx\\ & =\frac{1}{b-a}\times {\left[\frac{x^3}{3}\right]}_a^b\\ & =\frac{1}{b-a}\times \frac{b^3-a^3}{3}\\ & =\frac{1}{b-a}\times \frac{(b-a)(a^2+ab+b^2)}{3}\\ & =\frac{a^2+ab+b^2}{3}\end{array}$$
$$\begin{array}{rl}E(X{)}^2& =(\frac{a+b}{2}{)}^2\\ & =\frac{a^2+2ab+b^2}{4}\end{array}$$
$$\begin{array}{rl}\text{Var}(X)& =E(X^2)-[E(X){]}^2\\ & =\frac{a^2+ab+b^2}{3}-\frac{a^2+2ab+b^2}{4}\\ & =\frac{4a^2+4ab+4b^2-3a^2-6ab-3b^2}{12}\\ & =\frac{a^2-2ab+b^2}{12}\\ & =\frac{(b-a{)}^2}{12}\end{array}$$

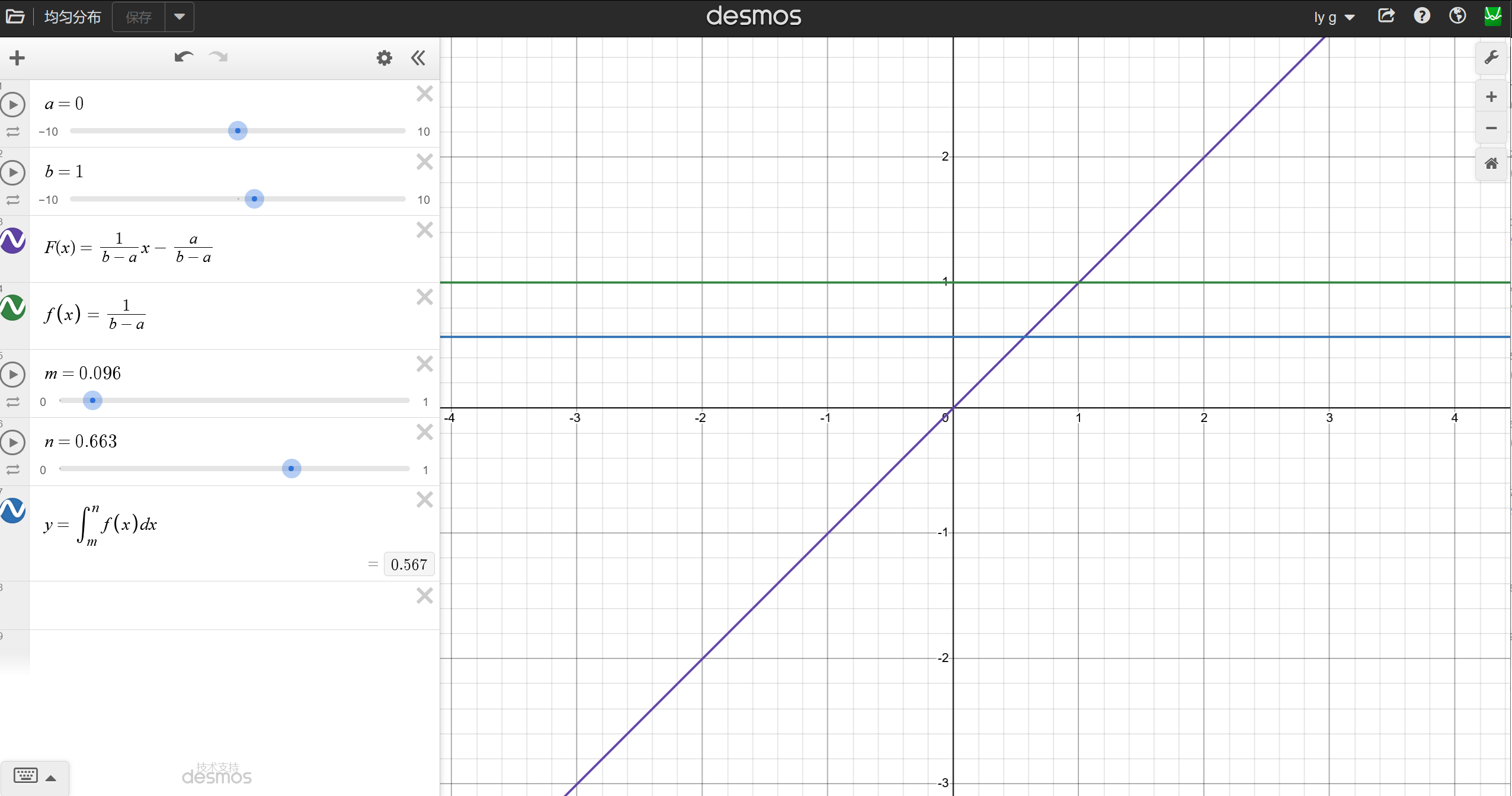
自己操作试试吧,可视化查看: 连续均匀分布

例题

从区间$[0,1]$中随机的选择一个数,求此数小于0.4的概率?
设随机变量$X$表示从区间$[0,1]$中随机选择的一个数,由题意得$X\sim U(0,1)$,求$P(X<0.4)$;
使用概率密度函数计算
$$P(X<0.4)={\int }_m^n\frac{1}{b-a}dx={\int }_0^{0.4}\frac{1}{1-0}dx=[x{]}_0^{0.4}=0.4$$
或使用累积分布函数计算
$$P(X<0.4)=F(0.4)=F(x)=\frac{x-a}{b-a}=\frac{0.4-0}{1-0}=0.4$$