目录
1. 多重线性回归
1.1 多元线性回归
1.2 向量化(矢量化)
1.3 多元线性回归的梯度下降算法
1.4 正规方程
2. 特征缩放
2.1 特征缩放
2.2 检查梯度下降是否收敛
2.3 学习率的选择
2.4 特征工程
2.5 多项式回归
3. 逻辑回归
3.1 Motivations
3.2 逻辑回归
3.3 决策边界
3.4 逻辑回归的代价函数
4. 梯度下降的实现
5. 过拟合
5.1 过拟合问题
5.2 解决过拟合问题
5.3 正则化代价函数
5.4 正则化线性回归
5.5 正则化逻辑回归
本次学习笔记基于吴恩达机器学习视频。
1. 多重线性回归
1.1 多元线性回归
矢量:

多元线性回归:具有多个特征的线性回归。
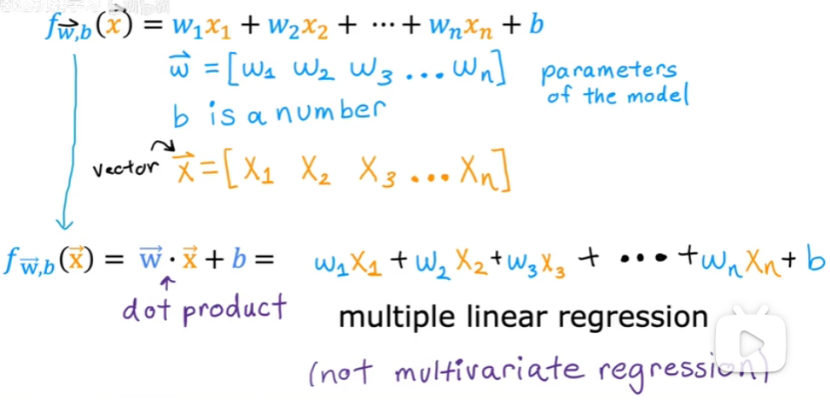
矢量化可以实现多元线性回归。
1.2 向量化(矢量化)
(1)向量化:

向量化优点:使得代码更加简洁;代码运行速度更快,如下图:

(2)向量化运行更快的原因
For循环与向量化的对比,如下图:
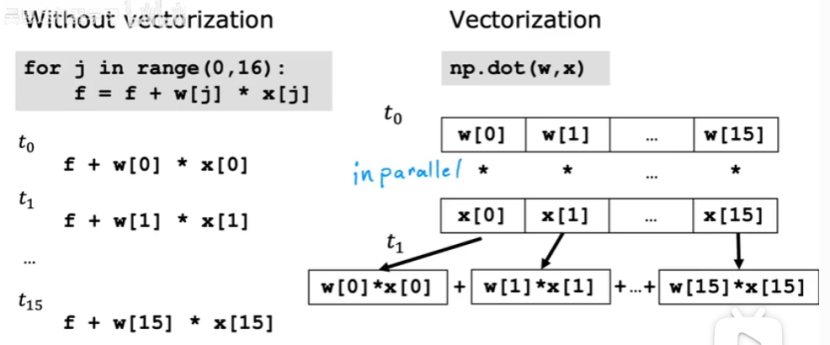
For循环是一步一步进行加法计算的。
向量化可以获取全部数据进行计算后,再用固定的硬件将全部相加起来。
例子:向量化如何帮助实现多元线性回归

向量化可以看成有16个数组,同时进行计算。
1.3 多元线性回归的梯度下降算法
可以用向量化来实现多元线性回归的梯度下降,如下图:

当多个特征时,梯度下降与只有一个特征时会稍有不同,如下图所示:
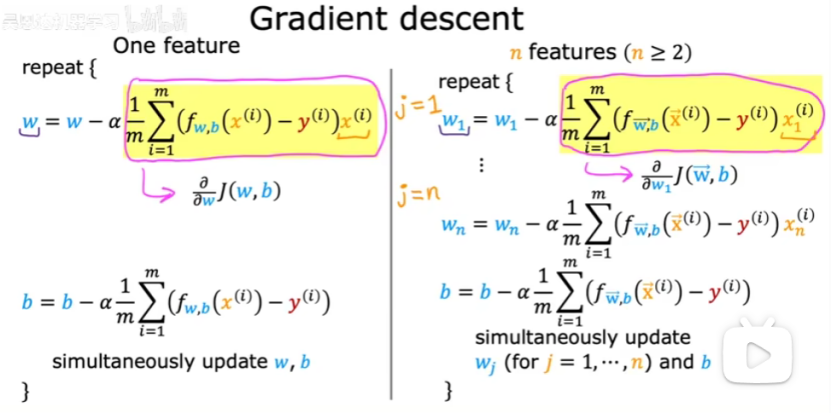
右边就是多元梯度下降算法。
1.4 正规方程
正规方程:寻找线性回归的w和b的替代方法的简短旁注。(仅适合线性回归,不需要迭代的梯度下降算法)
缺点:不能推广到其他学习算法;特征数量n很大时,正规方程也相当慢。
2. 特征缩放
2.1 特征缩放
(1)特征缩放:使梯度下降更快。
当一个特征的取值范围很大时,一个好的模型更可能会选择一个相对较小的参数值。
当一个特征的取值范围比较小时,一个好的模型更可能会选择一个相对较大的参数值。
当你有不同特征取值范围差异很大时,可能导致梯度下降运行缓慢。可以重新缩放不同的特征,使他们都在相似的范围内取值,可以加快梯度下降的速度。
(2)如何实现特征缩放以处理取值范围非常不同的特征,并且将他们缩放到具有可比的取值范围?
①都除以最大值
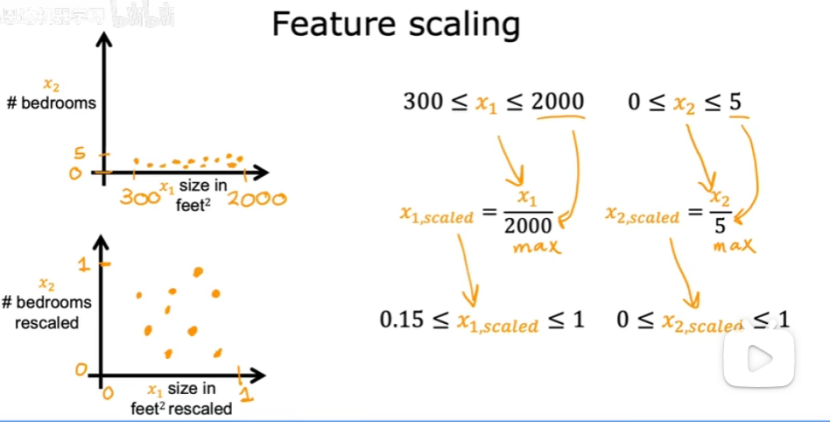
②均值归一化(将所有数据都集中在0附近)。
找到训练集上x1的均值,所有数减去均值,再除以差值。
找到训练集上x2的均值,所有数减去均值,再除以差值。

③z-score归一化(计算每个特征的均值和标准差)
每个x1减去均值再除以标准差。
每个x2减去均值再除以标准差。
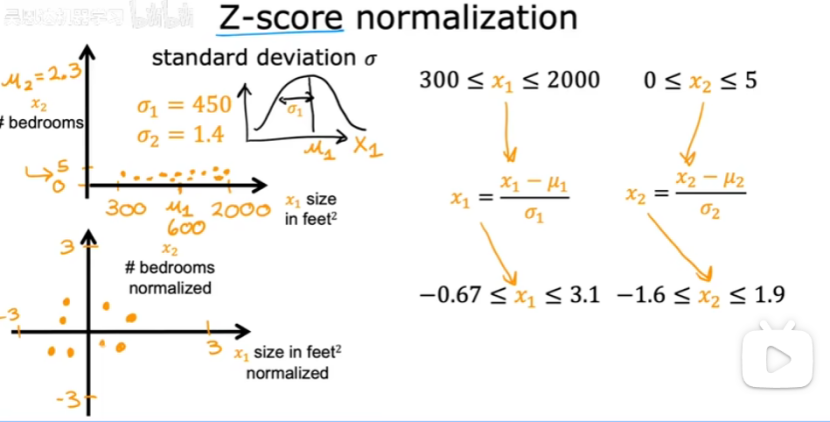
(3)特征的取值:

2.2 检查梯度下降是否收敛
(1)学习曲线
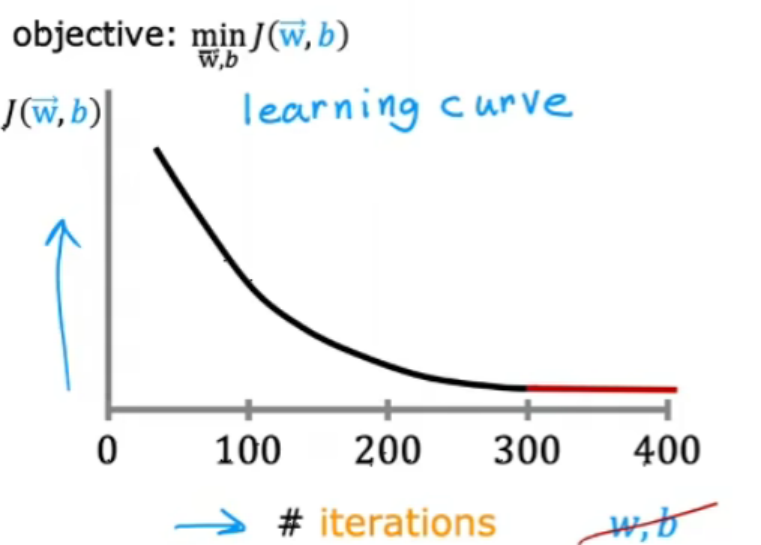
如果梯度下降正常工作,那么代价j应该在每次迭代后都减少。
如果j在一次迭代增加,那么意味着要么是a选择不当(a太大)或者代码中有错误。
当迭代到达300次时,代价j开始趋于平稳,不再有太大下降。到达400次时,梯度下降差不多已经收敛。
(2)检查梯度下降是否收敛的方法
①观察学习曲线,可以检查梯度下降是否收敛。
梯度下降收敛所需的迭代次数在不同的情况下可能会有很大的差异。
②使用自动收敛测试
设置一个变量epsilon,表示一个小数。如果在一次迭代中,代价j的减少量小于这个epsilon,则很可能看到学习曲线的平坦部分,可以宣布收敛。
但是找到epsilon很困难,所以推荐查看学习曲率来检查梯度下降是否收敛。
2.3 学习率的选择
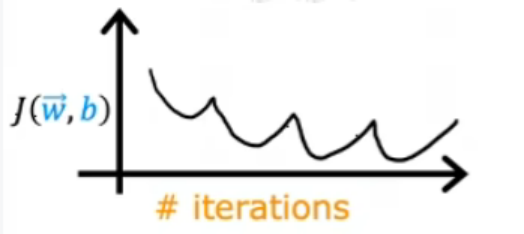
出现上图的原因是可能代码出现错误或者学习率太大。
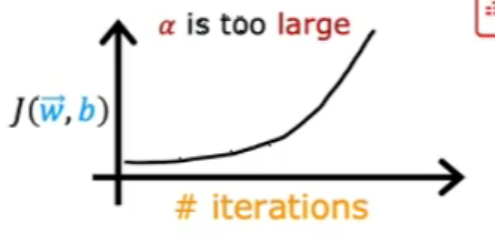
上图是因为学习率太大导致的,可以减少学习率。(或者代码的错误)
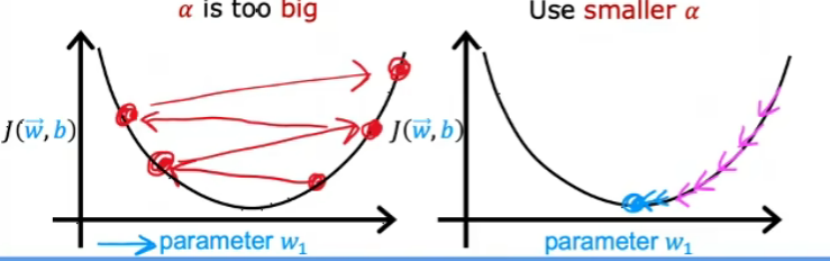
当学习率太大时,可能会出现上面左图无法收敛的情况,可以减少学习率。
如果把学习率设置成一个很小很小的数值,但是学习曲线还是会出现上升的情况,表示代码出现了错误。
但是学习率太小时,需要很多次迭代才可以达到收敛。
选择学习率的技巧:
先选择一个很小很小的数值,然后每一次扩大3倍,继续尝试,直到找到最合适的学习率可以使得学习曲线下降的比较快且平稳。
2.4 特征工程
使得多元线性回归更加强大-->选择自定义的特征
如何选择或设计最合适的特征用于学习:可以利用对问题的知识或者直觉来设计新特征,通常通过转化或组合问题的原始特征,以便让学习算法更容易做出预测。
2.5 多项式回归
多项式回归可以拟合曲线,是将特征x提升到任何平方或者开根号。这样的话更需要注意特征缩放。
3. 逻辑回归
3.1 Motivations
二元分类:结果只有两个可能的分类/类别
如何构建分类算法:可以看决策边界(如下图的垂直线)
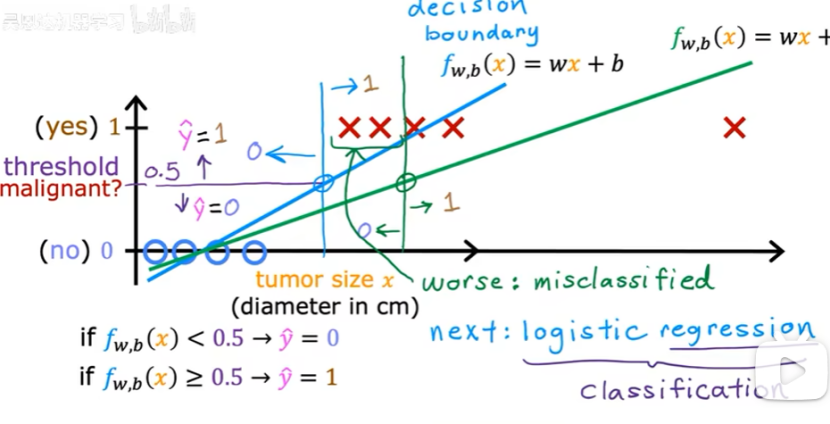
3.2 逻辑回归
逻辑回归:用于分类(用于解决输出标签y为0或1的二元分类问题)
Sigmoid函数:

f的结果表示等于1的概率。
3.3 决策边界
f>=0.5时(z>=0时/wx+b>=0时),y=1;
f<0.5时(z<0时/wx+b<0时),y=0;
决策边界:z=wx+b=0
例子:决策边界为直线时
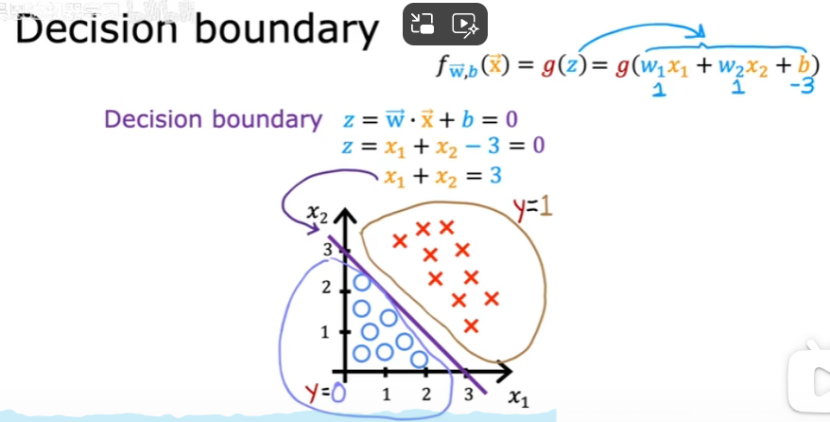
例子:决策边界为曲线时

3.4 逻辑回归的代价函数
为什么平方误差成本函数不是逻辑回归的理想成本函数?
因为梯度下降时会遇到很多局部最小值,如下图:
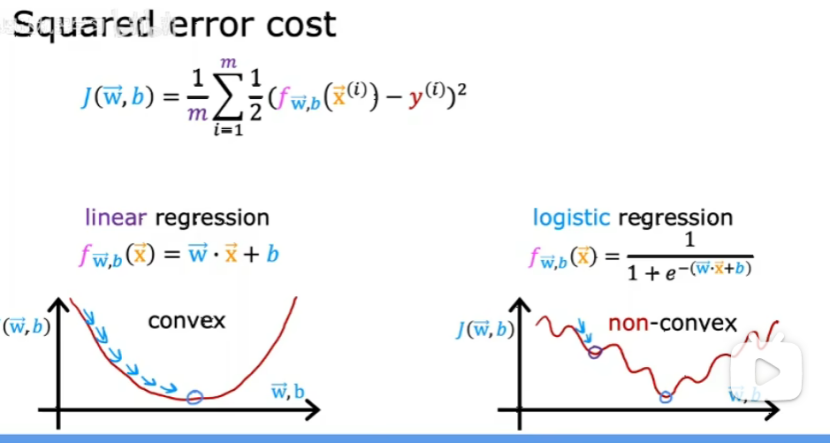
损失函数:
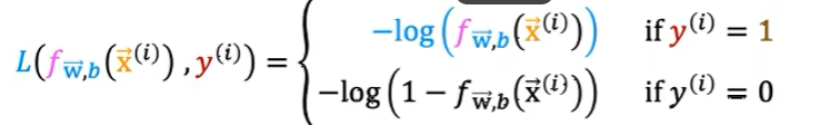
①Y=1时,预测值接近1时,损失最小,如下图:
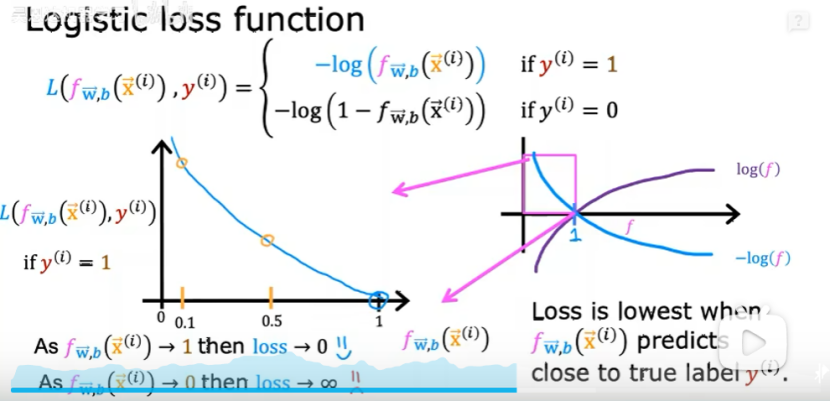
②Y=0时,预测值接近0时,损失最小,如下图:
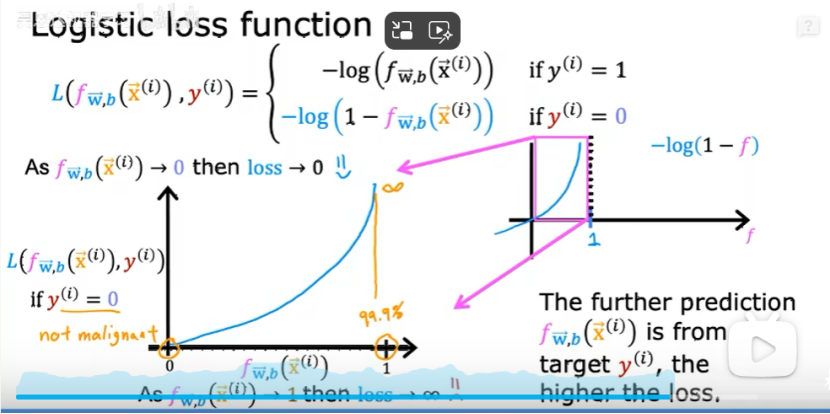
损失函数的简化版公式如下:
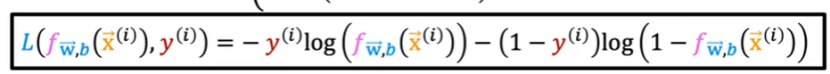
训练逻辑回归的代价函数如下:
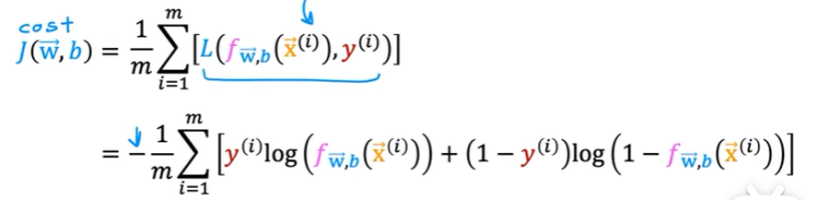
4. 梯度下降的实现
如何找到一个合适的w和b?

把右侧带入左侧,得到下面:

上面与线性回归的区别:函数f(x)的定义已经改变了,如下图:

5. 过拟合
5.1 过拟合问题
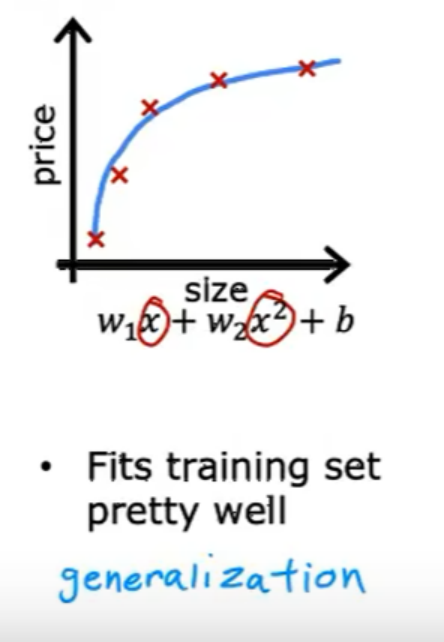
泛化:对于全新的例子也能做出良好的预测。
下面是没有过拟合也没有欠拟合的情况:
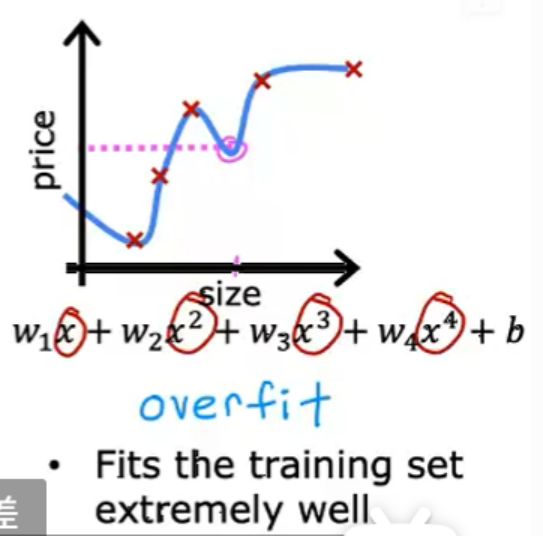
过拟合/算法有高方差:模型太复杂,导致在训练集上表现很好,但在测试集上泛化能力差。如下图情况:
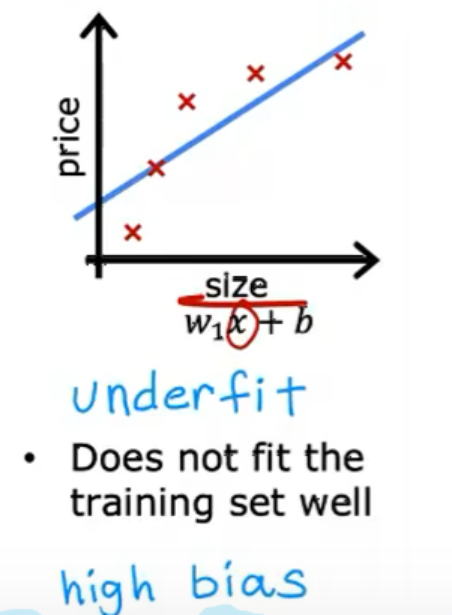
欠拟合:模型太过简单,无法很好拟合训练数据。如下图情况:
5.2 解决过拟合问题
(1)收集足够多的训练数据,可以保证尽管是过拟合的模型,也可以表现很好。
(2)减少多项式的特征:进行特征选择(选择最重要的几个特征集)
(3)正则化:更温和的减少某些特征影响的方法,而不需要去除他们。(将特征的参数大小减小)
一般只正则化w1~wn,而不正则化b。
5.3 正则化代价函数
当特征的参数较小时,模型比较简单,不容易产生过拟合的情况。
当不知道哪些参数是重要的时候,就惩罚所有特征参数;

如果正则率(![]() )=0,则表示没有正则化
)=0,则表示没有正则化
如果正则率特别大,f(x)约等于b;学习算法会拟合出一条水平直线,并出现欠拟合。
5.4 正则化线性回归

带入后如下:
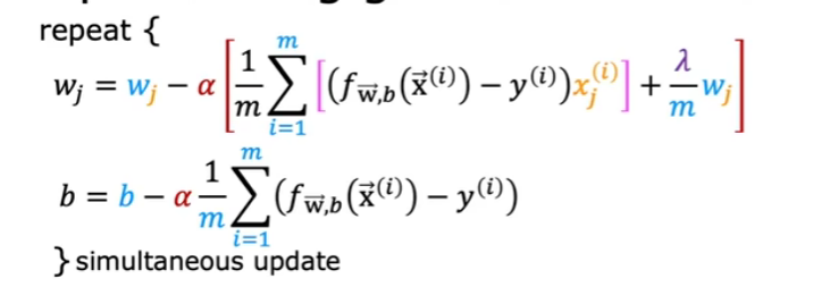
注意:只正则化w,不正则化b。
5.5 正则化逻辑回归
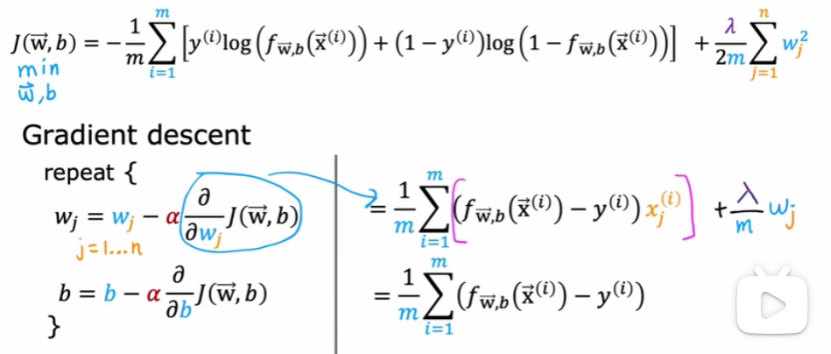

)

















