简单黑盒对抗攻击

Chuan Guo ¹ Jacob R. Gardner ² Yurong You ¹ Andrew Gordon Wilson ¹ Kilian Q. Weinberger ¹

摘要

我们提出了一种在黑盒（black-box）场景下构建对抗样本（adversarial images）的极其简单的方法。与白盒（white-box）场景相比，构建黑盒对抗样本额外受到查询预算（query budget）的限制，而高效的攻击方法至今仍是一个开放性问题。仅需模型输出连续值置信度分数（confidence scores）这一温和假设，我们高度查询高效的算法采用了以下简单的迭代原理：我们从预定义的标准正交基（orthonormal basis）中随机采样一个向量，然后将其加到目标图像上或从中减去。尽管方法简单，所提出的方法既可用于非定向攻击（untargeted attacks），也可用于定向攻击（targeted attacks）——在这两种设置下都实现了前所未有的查询效率。我们在包括 Google Cloud Vision API 在内的多个真实世界场景中证明了我们算法的有效性和效率。我们认为，我们提出的算法应作为未来黑盒攻击的强大基线，特别是因为它速度极快，其实现只需不到 20 行 PyTorch 代码。

1 引言

随着机器学习系统在众多应用领域的普及，这些系统在面对恶意对手（malicious adversaries）时的安全性已成为一个重要的研究领域。许多近期研究表明，通过对输入进行人眼无法察觉的微小改动，机器学习模型输出的决策可以被任意改变（Carlini & Wagner; Szegedy et al., 2014）。这些对机器学习模型的攻击可以根据对手的能力进行分类。白盒（White-box) 攻击要求对手完全了解目标模型，而 黑盒（black-box) 攻击则仅需要向目标模型发出查询（queries），这些查询可能返回完整或部分信息。

似乎所有用于自然图像分类的模型都容易受到白盒攻击（Athalye et al., 2018），这表明自然图像往往靠近机器学习分类器学习到的决策边界（decision boundaries）。尽管常常被误解为神经网络的特性（Szegedy et al., 2014），但对抗样本（adversarial examples）的脆弱性很可能是高维空间中、在大多数数据分布下分类器不可避免的属性（Fawzi et al., 2018; Shafahi et al., 2018）。

如果对抗样本（几乎）总是存在，那么攻击一个分类器就变成了在目标图像周围一个小空间内的搜索问题。在白盒场景中，这种搜索可以通过梯度下降（gradient descent）有效地引导（Szegedy et al., 2014; Carlini & Wagner; Madry et al., 2017）。然而，黑盒威胁模型（black-box threat model）在许多场景中更具适用性。在此情况下，向模型发出查询可能会产生显著的时间和金钱成本，因此向模型发出的黑盒查询次数成为衡量攻击算法效率的重要指标。成本过高或容易被查询限制（query limiting）击败的攻击，其安全风险低于高效攻击。迄今为止，尽管该领域近期有大量研究工作（Chen et al., 2017; Brendel et al., 2017; Cheng et al., 2018; Guo et al., 2018; Tu et al., 2018; Ilyas et al., ），最著名的黑盒攻击的平均查询次数仍然很高。最有效和最复杂的攻击通常仍需要数万甚至数十万次查询。寻找一种查询高效的黑盒攻击方法仍然是一个开放性问题。

像 Clarifai 或 Google Cloud Vision 这样的机器学习服务只允许通过 API 调用来访问模型的预测结果，因此属于黑盒类别。这些服务不发布任何内部细节，如训练数据和模型参数；然而，它们的预测会返回连续值的置信度分数。在本文中，我们提出了一种简单而高效的黑盒攻击方法，它利用这些置信度分数，基于一个非常简单的直觉：如果到决策边界的距离很小，那么我们不必过分在意我们沿着哪个确切方向朝它移动。具体来说，我们反复从预先指定的一组正交搜索方向中随机选取一个方向，使用置信度分数检查它是朝向还是背离决策边界，然后通过将该向量加到图像上或从中减去来扰动图像。每次更新都会使图像进一步远离原始图像并靠近决策边界。

我们为方法的有效性提供了一些理论见解，并评估了各种正交搜索子空间。与 Guo et al. (2018) 类似，我们观察到将搜索限制在离散余弦变换（Discrete Cosine Transform, DCT）基的低频端（low frequency end）尤其查询高效。此外，我们通过实验证明，我们的方法在成功率（success rate）上与最先进的黑盒攻击算法相当，但所需的黑盒查询次数却低得前所未有。由于其简单性——可以在 PyTorch 中用不到 20 行代码¹实现——我们认为我们的方法是图像对抗攻击的一个新的、可能令人惊讶的强大基线，我们将其称为简单黑盒攻击（Simple Black-box Attack, SimBA）。

2 背景

对抗样本的研究关注机器学习模型对输入微小变化的鲁棒性（robustness）。图像分类任务被定义为成功预测人类在图像中看到的内容。自然地，对图像的微小改动，小到人类无法察觉的程度，不应影响标签和预测。我们可以将这种鲁棒性形式化如下：给定一个模型 $h$ 和一个输入标签对 $(\mathbf{x},y)$，在该输入上模型能正确分类 $h(\mathbf{x})=y$，如果对于所有满足 $d({\mathbf{x}}^{\prime },\mathbf{x})\le \rho$ 的 ${\mathbf{x}}^{\prime }$ 都有 $h({\mathbf{x}}^{\prime })=y$，则称 $h$相对于可感知性度量$d(\cdot ,\cdot )$是 $\rho$-鲁棒的（$\rho$-robust）。

度量 $d$ 通常用 $L_0$、$L_2$ 和 $L_{\infty }$ 距离（distances）来近似，以衡量干净输入$\mathbf{x}$ 和扰动输入 ${\mathbf{x}}^{\prime }$ 之间的视觉差异程度。遵循 (Moosavi-Dezfooli et al., 2016; Moosavi-Dezfooli et al., 2017)，在本文的剩余部分，除非另有说明，我们将使用 $d(\mathbf{x},{\mathbf{x}}^{\prime })=\Vert \mathbf{x}-{\mathbf{x}}^{\prime }{\Vert }_2$ 作为可感知性度量。因此，从几何上讲，不可察觉变化的区域被定义为以输入图像 $\mathbf{x}$ 为中心、半径为 $\rho$的小超球面（hypersphere）。

最近，许多研究表明，即使对于非常小的 $\rho$值，学习到的模型也存在非鲁棒性方向（Moosavi-Dezfooli et al., 2016; Carlini & Wagner, ）。Fawzi et al. (2018); Shafahi et al. (2018) 通过理论证明对抗样本在高维空间中是固有的（inherent）来验证了这一观点。这些发现激发了寻找对抗方向 $\delta$ 的问题，该方向会改变模型对扰动输入 ${\mathbf{x}}^{\prime }=\mathbf{x}+\delta$ 的决策。

定向攻击和非定向攻击。 对手最简单的成功条件是改变模型原有的正确预测为任意类别，即 $h({\mathbf{x}}^{\prime })\ne y$。这被称为非定向攻击（untargeted attack）。相反，定向攻击（targeted attack） 旨在构建 ${\mathbf{x}}^{\prime }$ 使得$h({\mathbf{x}}^{\prime })=y^{\prime }$，其中$y^{\prime }$ 是某个选定的目标类别。为简洁起见，我们将在讨论中重点关注非定向攻击，但我们论文中的所有论点也适用于定向攻击。我们在第 4 节中包含了两种攻击类型的实验结果。

损失最小化。 由于模型输出离散决策，寻找对抗扰动来改变模型的预测首先是一个离散优化问题。然而，定义一个代理损失（surrogate loss）${\ell }_y(\cdot )$ 通常很有用，它衡量模型 $h$ 将输入分类为类别 $y$ 的确定性程度。因此，对抗扰动问题可以表述为以下约束连续优化问题，以最小化模型的分类确定性：

$$\underset{\delta }{\min }{\ell }_y(\mathbf{x}+\delta )\text{ subject to }\Vert \delta {\Vert }_2<\rho .$$
当模型 $h$ 输出与每个类别相关的概率 $p_h(\cdot \mid \mathbf{x})$ 时，一个常用的对抗损失是类别 $y$ 的概率：${\ell }_y({\mathbf{x}}^{\prime })=p_h(y\mid {\mathbf{x}}^{\prime })$，本质上是最小化正确分类的概率。对于目标标签 $y^{\prime }$ 的定向攻击，常见的选择是 ${\ell }_{y^{\prime }}({\mathbf{x}}^{\prime })=-p_h(y^{\prime }\mid {\mathbf{x}}^{\prime })$，本质上是最大化被错误分类为$y^{\prime }$ 类的概率。

个人学习批注：
核心问题：模型输出是离散的（类别标签），直接改变它是个困难的离散优化问题。
解决方案：引入一个连续可优化的“代理损失函数” ${\ell }_y(\cdot )$。这个函数量化模型对原始正确类别 $y$ 的“确信度”。
优化目标：将问题转化为一个带约束的连续优化问题：在扰动 $\delta$ 的$L_2$ 范数小于 $\rho$(保证扰动微小/不可察觉) 的限制下，最小化这个代理损失函数。
$$\underset{\delta }{\min }{\ell }_y(\mathbf{x}+\delta )\text{ subject to }\Vert \delta {\Vert }_2<\rho .$$
常用代理损失函数 (基于概率输出)：

• 非定向攻击： 最小化模型对原始正确类别 $y$ 的预测概率 ${\ell }_y({\mathbf{x}}^{\prime })=p_h(y\mid {\mathbf{x}}^{\prime })$。目标：让模型不再确信这是原类。
• 定向攻击： 最大化模型对指定目标类别 $y^{\prime }$ 的预测概率。等价于最小化该概率的负值 ${\ell }_{y^{\prime }}({\mathbf{x}}^{\prime })=-p_h(y^{\prime }\mid {\mathbf{x}}^{\prime })$。目标：让模型高度确信这是目标类。

白盒威胁模型。 根据应用领域的不同，攻击者可能对目标模型 $h$ 有不同程度的了解。在白盒（white-box) 威胁模型下，分类器 $h$ 是提供给对手的。在这种情况下，一种强大的攻击策略是对对抗损失 ${\ell }_y(\cdot )$ 或其近似值执行梯度下降（gradient descent）。为了确保更改保持不可察觉，可以通过提前停止（early stopping）(Goodfellow et al., 2015; Kurakin et al., 2016) 或将范数 $\Vert \delta {\Vert }_2$ 直接作为正则化项（regularizer）或约束纳入损失优化（Carlini & Wagner, ）来控制扰动范数。

黑盒威胁模型。 可以说，对于许多现实世界场景，白盒假设可能不切实际。例如，模型 $h$ 可能作为 API 公开给公众，仅允许对输入进行查询。在攻击 Google Cloud Vision 和 Clarifai 等机器学习云服务时，这种场景很常见。这种黑盒（black-box） 威胁模型对对手来说更具挑战性，因为梯度信息可能无法用于指导寻找对抗方向 $\delta$，并且每次向模型查询都会产生时间和金钱成本。因此，对手面临一个额外的目标，即在成功构建一个不可察觉的对抗扰动的同时，最小化对 $h$ 的黑盒查询次数。略微滥用符号，这提出了一个修改后的约束优化问题：

$$\underset{\delta }{\min }{\ell }_y(\mathbf{x}+\delta )\text{subject to:}\Vert \delta {\Vert }_2<\rho ,\text{queries}\le B$$

其中 $B$ 是优化期间允许的查询次数的固定预算（budget）。对于进行查询的迭代方法，预算 $B$ 限制了算法可以进行的迭代次数，因此要求攻击算法非常快地收敛到解。

3 一种简单的黑盒攻击

算法 1：
1: procedure SimBA(x, y, Q, ε)       # 输入：原始图像x，真实标签y，正交方向集Q，步长ε
2:   δ = 0                           # 初始化对抗扰动δ为零向量
3:   p = p_h(y | x)                  # 查询模型，获取原始图像x的预测概率p
4:   while p_y == max_{y'} p_{y'}:   # 循环条件：当前预测y仍是最高概率类别
5:     q = RandomPickWithoutReplacement(Q)  # 从Q中无放回随机选取一个正交方向q
6:     for α ∈ {ε, -ε}:              # 尝试正向/负向步长（±ε）
7:       p' = p_h(y | x + δ + αq)    # 计算扰动后图像(x+δ+αq)的预测概率p'
8:       if p'_y < p_y:              # 若新概率p'小于当前p（即y的概率下降）
9:         δ = δ + αq                # 更新扰动：沿方向q叠加步长α
10:        p = p'                    # 更新当前概率为p'
11:        break                     # 跳出当前方向q的尝试，继续下一方向
12: return δ                         # 返回生成的对抗扰动δ

我们假设有一张图像 $\mathbf{x}$，一个黑盒神经网络 $h$ 将其分类为 $h(\mathbf{x})=y$，并给出预测置信度或输出概率 $p_h(y\mid \mathbf{x})$。我们的目标是找到一个小的扰动 $\delta$，使得预测 $h(\mathbf{x}+\delta )\ne y$。尽管在黑盒设置中缺乏梯度信息，我们主张输出概率的存在可以作为指导搜索对抗图像的强大代理（proxy）。

算法。 我们方法背后的直觉很简单（见算法 1 中的伪代码）：对于任何方向 $\mathbf{q}$ 和某个步长 $ϵ$，$\mathbf{x}+ϵ\mathbf{q}$ 或 $\mathbf{x}-ϵ\mathbf{q}$ 中的一个很可能降低 $p_h(y\mid \mathbf{x})$。因此，我们反复选取随机方向 $\mathbf{q}$，然后加上或减去它们。为了最小化对 $h(\cdot )$ 的查询次数，我们总是先尝试加上 $ϵ\mathbf{q}$。如果这降低了概率 $p_h(y\mid \mathbf{x})$，我们就执行这一步；否则，我们尝试减去 $ϵ\mathbf{q}$。这个过程平均每次更新需要 1.4 到 1.5 次查询（取决于数据集和目标模型）。我们提出的方法——简单黑盒攻击（Simple Black-box Attack, SimBA）——输入目标图像标签对 $(\mathbf{x},y)$、一组标准正交候选向量 $Q$ 和一个步长 $ϵ>0$。为简单起见，我们均匀随机选取 $\mathbf{q}\in Q$。为了保证最大的查询效率，我们确保没有两个方向相互抵消从而削弱进展，或者相互叠加并不成比例地增加 $\delta$ 的范数。为此，我们无放回（without replacement） 地选取$\mathbf{q}$，并限制 $Q$ 中的所有向量都是*标准正交（orthonormal）*的。正如我们稍后展示的，这保证了在 $T$ 次更新后扰动范数为 $\Vert \delta {\Vert }_2=\sqrt{T}ϵ$。SimBA 唯一的超参数（hyper-parameters）是正交搜索向量集 $Q$ 和步长 $ϵ$。

笛卡尔基（Cartesian basis）。 正交搜索方向集 $Q$的一个自然首选是标准基 $Q=I$，这对应于直接在像素空间中执行我们的算法。本质上，每次迭代我们都在增加或减少一个随机选择的单个像素的一种颜色。在这种基中进行攻击对应于 $L_0$-攻击，其中对手旨在更改尽可能少的像素。

离散余弦基（Discrete cosine basis）。 最近的工作发现，低频空间中的随机噪声更可能具有对抗性（Guo et al., 2018）。为了利用这一事实，我们遵循 Guo et al. (2018) 并建议利用离散余弦变换（Discrete Cosine Transform, DCT）。离散余弦变换是一种标准正交变换，它将二维图像空间 ${\mathbb{R}}^{d\times d}$ 中的信号映射到对应于余弦波函数幅度的频率系数（frequency coefficients）。在下文中，我们将 DCT 提取的标准正交频率集合称为 $Q_{\mathrm{DCT}}$。虽然完整的方向集 $Q_{\mathrm{DCT}}$ 包含 $d\times d$ 个频率，但我们只保留最低频率方向的一小部分 $r$，以使对抗扰动位于低频空间中。

通用基（General basis）。 总的来说，我们相信我们的攻击可以与任何标准正交基一起使用，前提是基向量可以被高效采样。这对于像 ImageNet 这样的高分辨率数据集尤其具有挑战性，因为每个标准正交基向量都具有 $d\times d$ 的维度。像 Gram-Schmidt 过程这样的迭代采样方法由于采样向量数量的线性内存成本而无法使用。因此，我们选择仅使用标准基向量和 DCT 基向量来评估我们的攻击，因为它们的效率和天然适合图像的特性。

学习率 $ϵ$。 给定任何搜索方向集 $Q$，某些方向可能比其他方向更能降低 $p_h(y\mid \mathbf{x})$。此外，输出概率 $p_h(y\mid \mathbf{x}+ϵ\mathbf{q})$在 $ϵ$ 上可能是非单调的。在图 1 中，我们绘制了在像素空间和 DCT 空间中随机采样的搜索方向上，概率的相对下降作为 $ϵ$的函数。这些概率对应于 ResNet-50 模型对 ImageNet 验证样本的预测。该图突显了一个有启发性的结果：概率 $p_h(y\mid \mathbf{x}\pm ϵ\mathbf{q})$ 在 $ϵ$ 上单调递减（decreases monotonically），具有惊人的一致性（跨越随机图像和向量 $\mathbf{q}$）！尽管某些方向最终会增加真实类别的概率，但该概率的预期变化是负的，且斜率相对陡峭。这意味着我们的算法对 $ϵ$ 的选择不太敏感，并且迭代将快速降低真实类别的概率。该图还表明，在 DCT 空间中的搜索往往导致比像素空间更陡峭的下降方向。正如我们在下一节所示，给定 $ϵ$ 和最大步数 $T$ 的选择，我们可以严格限制扰动的最终 $L_2$-范数，因此 $ϵ$ 的选择主要取决于相对于 $\Vert \delta {\Vert }_2$ 的预算考虑（budget considerations）。

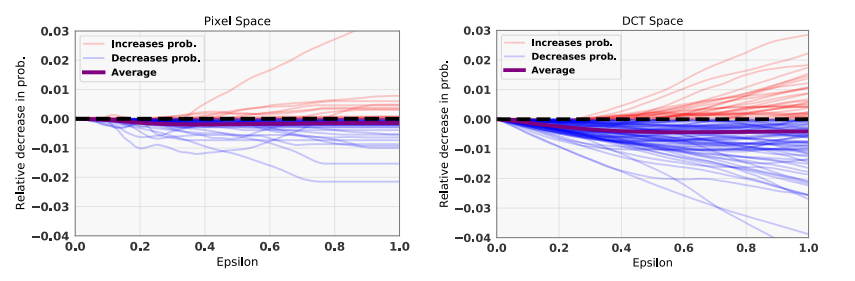
图 1: 当以步长 $ϵ$加上或减去随机选取的基方向 $\mathbf{q}$（取损失下降更大的那个）时，预测类别概率的变化图。左图显示像素空间，右图显示低频 DCT 空间。平均变化（紫线）在 $ϵ$ 上几乎是线性的，当方向在 DCT 空间采样时斜率更陡。此外，在 DCT 空间采样的方向中有 98% 的方向具有$-\mathbf{q}$ 或 $\mathbf{q}$ 下降，而在像素空间中只有 73% 是下降的。

预算考虑。 通过利用基 $Q$ 的标准正交性，我们可以严格限制 $\delta$ 的范数。每次迭代中，一个基向量要么被加上，要么被减去，要么被丢弃（如果两个方向都不能降低输出概率）。令 αt∈{−ϵ,0,ϵ}\alpha_{t}\in\{-\epsilon,0,\epsilon\}αt​∈{−ϵ,0,ϵ} 表示在第$t$步选择的搜索方向的符号，因此

$${\delta }_{t+1}={\delta }_t+{\alpha }_t{\mathbf{q}}_t.$$

我们可以递归地展开 ${\delta }_{t+1}={\delta }_t+{\alpha }_t{\mathbf{q}}_t$。通常，经过 $T$ 步后的最终扰动 ${\delta }_T$可以写成这些单个搜索方向的总和：

$${\delta }_T=\sum _{t=1}^T{\alpha }_t{\mathbf{q}}_t.$$

由于方向 ${\mathbf{q}}_t$ 是正交的，对于任何 $t\ne t^{\prime }$都有 ${\mathbf{q}}_t^{\top }{\mathbf{q}}_{t^{\prime }}=0$。因此我们可以计算对抗扰动的 $L_2$-范数：

$$\Vert {\delta }_T{\Vert }_2^2={\Vert \sum _{t=1}^T{\alpha }_t{\mathbf{q}}_t\Vert }_2^2=\sum _{t=1}^T\Vert {\alpha }_t{\mathbf{q}}_t{\Vert }_2^2=\sum _{t=1}^T{\alpha }_t^2\Vert {\mathbf{q}}_t{\Vert }_2^2\le T{ϵ}^2.$$

这里，第二个等式源于 ${\mathbf{q}}_t$ 和 ${\mathbf{q}}_{t^{\prime }}$ 的正交性，最后一个不等式是紧的（tight）——如果所有查询都导致 $ϵ$ 或 $-ϵ$的步长。因此，在$T$ 次迭代后，对抗扰动的 $L_2$-范数最多为 $\sqrt{T}ϵ$。这个结果适用于任何标准正交基（例如 $Q_{\text{DCT}}$）。

我们的分析突显了一个重要的权衡：对于查询受限的场景，我们可以通过设置更高的 $ϵ$ 来减少迭代次数，但这会带来更高的扰动 $L_2$-范数。如果低范数解更可取，降低 $ϵ$ 将在相同的 $L_2$-范数下允许二次方更多的查询。对这种权衡进行更彻底的理论分析可以提高查询效率。

4 实验评估

在本节中，我们针对一系列具有竞争力的黑盒攻击算法评估我们的攻击：边界攻击（Boundary Attack）(Brendel et al., 2017)、Opt攻击（Opt attack）(Cheng et al., 2018)、低频边界攻击（Low Frequency Boundary Attack, LFBA）(Guo et al., 2018)、AutoZOOM (Tu et al., 2018)、QL攻击（QL attack）(Ilyas et al., ) 和 Bandits-TD 攻击（Bandits-TD attack）(Ilyas et al., )。评估黑盒对抗攻击有三个维度：优化问题找到可行点的频率（成功率，success rate）、所需的查询次数（$B$）以及产生的扰动范数（$\rho$）。

4.1 设置

我们首先在 ImageNet 上评估我们的方法。我们从 ImageNet 验证集中采样 1000 张图像，这些图像最初被正确分类，以避免人为夸大成功率。由于每个类别的预测概率都可用，我们在非定向攻击中最小化正确类别的概率作为对抗损失，在定向攻击中最大化目标类别的概率。对于所有定向攻击，我们均匀随机采样一个目标类别。

接下来，我们在攻击 Google Cloud Vision API 的现实场景中评估 SimBA。由于基线方法可能每张图像花费高达 150 美元²的极端预算要求，这里我们只与 LFBA 进行比较，我们发现 LFBA 是查询效率最高的基线。

在我们的实验中，我们将 SimBA 和 SimBA-DCT 的非定向攻击最大迭代次数限制为 $T=10,000$，定向攻击为$T=30,000$。对于 SimBA-DCT，我们保留所有频率的前 $1/8$，并在未成功耗尽可用频率时额外添加 $1/32$ 的频率。对于两种方法，我们都使用固定步长 $ϵ=0.2$。

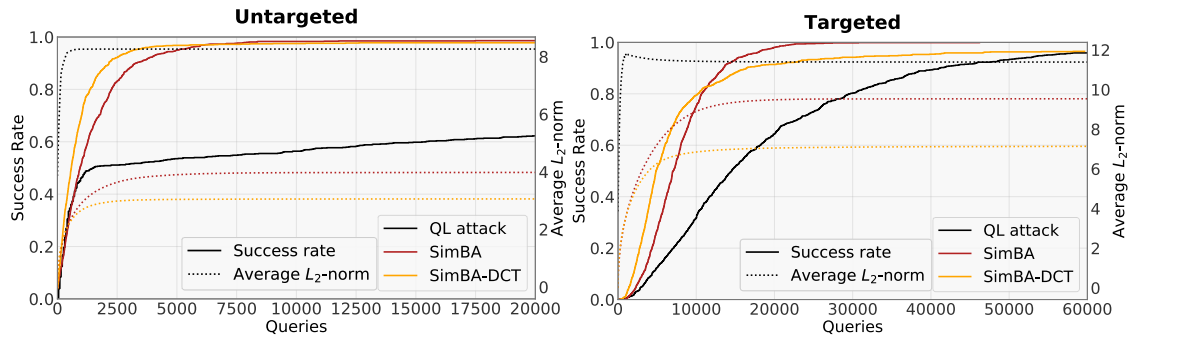
图 2: 非定向（左）和定向（右）攻击的成功率与平均$L_2$-范数相对于模型查询次数的比较。横轴显示模型查询次数。在非定向和定向场景中，SimBA 和 SimBA-DCT 的成功率增长都显著快于 QL-attack。两种方法也实现了比 QL-attack 更低的平均 $L_2$-范数。请注意，尽管 SimBA-DCT 初始收敛更快，但其最终成功率低于 SimBA。

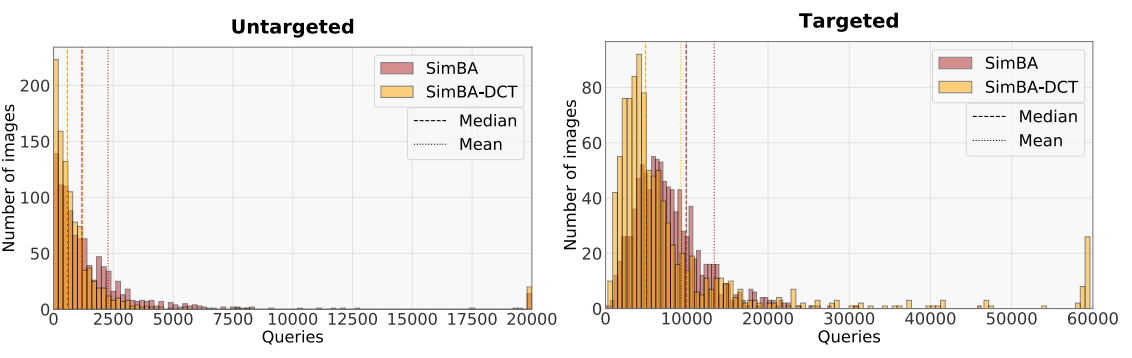
图 3: 成功攻击所需的查询次数直方图（超过 1000 张目标图像）。SimBA-DCT 高度右偏，表明只有少数图像需要超过少量查询。对于非定向攻击，SimBA-DCT 所需的中位数（median）查询次数仅为 582。然而，限制在低频基导致 SimBA-DCT 在 $60,000$ 次查询后未能找到成功的对抗图像，而 SimBA 可以始终如一地实现 $100\%$ 的成功率。

4.2 ImageNet 结果

成功率比较（图 2）。 我们通过绘制平均成功率相对于查询次数的图表，展示了我们方法的查询效率与 QL 攻击（可以说是迄今为止最先进的黑盒攻击方法）的比较。图 2 显示了非定向攻击和定向攻击的比较。虚线显示了整个优化过程中平均$L_2$-范数的进展。在非定向和定向场景中，SimBA 和 SimBA-DCT 都实现了成功率显著更快的增长。两种方法的平均 $L_2$-范数也显著更低。

查询分布（图 3）。 在图 3 中，我们绘制了 SimBA 和 SimBA-DCT 在 1000 张随机图像上的模型查询次数的直方图。请注意，分布是高度右偏（right skewed）的，因此中位数查询次数是比平均查询次数更具代表性的聚合统计量。SimBA 和 SimBA-DCT 的中位数查询次数分别仅为 944 和 582。在定向攻击情况下，SimBA-DCT 仅需 $4,854$次中位数查询即可构建对抗扰动，但对于大约 $2.5\%$的图像在$60,000$次查询后未能成功。相比之下，SimBA 实现了 $100\%$ 的成功率，中位数查询次数为 $7,038$。

这个结果显示了在选择标准正交基$Q$ 时的一个基本权衡。将 SimBA-DCT 限制在仅低频 DCT 基向量上，对于大多数图像会导致更快的平均下降速率，但对于某些图像可能无法产生对抗扰动。Guo et al. (2018) 在基于优化的白盒攻击中也观察到了这种现象。在每张图像的基础上找到合适的频谱进行操作，可能是进一步提高黑盒攻击算法查询效率和成功率的关键。我们将这个有前景的方向留给未来的工作。

聚合统计（表 1）。 表 1 计算了不同攻击算法在模型查询次数、成功率和扰动 $L_2$-范数方面的聚合统计量。我们使用默认超参数重现了 LFBA、QL-attack 和 Bandits-TD 的结果，并呈现了原始作者论文中报告的 Boundary Attack³、Opt-attack 和 AutoZOOM 的数据。目标模型是一个预训练的 ResNet-50 (He et al., 2016) 网络，除了 AutoZOOM 使用的是 Inception v3 (Szegedy et al., 2016) 网络。其中一些攻击在更困难的仅标签（label-only）设置下运行（即仅观察到预测的标签），这可能会因观察到部分信息而影响其查询效率。尽管如此，为了完整性，我们在表中包含了这些方法。

表中的三列显示了评估黑盒攻击的所有相关指标。理想情况下，一次攻击应该经常成功，构建具有低 $L_2$ 范数的扰动，并且以非常少的查询完成。通过降低成功率或增加扰动范数可以人为地减少模型查询次数。为了确保公平比较，我们强制要求我们的方法达到接近 $100\%$ 的成功率，并比较其他两个指标。请注意，边界攻击和 LFBA 的成功率始终是 $100\%$，因为这两种方法都从非常大的扰动开始以保证错误分类，然后逐渐减小扰动范数。

SimBA 和 SimBA-DCT 的平均 $L_2$-范数都 显著低于（significantly lower） 所有基线方法。对于非定向攻击，我们的方法需要比最强的基线方法——Bandits-TD（仅达到 $80\%$ 成功率）少 3-4 倍的查询（分别为 $1,665$ 和 $1,232$）。对于定向攻击（右表），所评估的方法更具可比性，但 SimBA 和 SimBA-DCT 仍然比 QL-attack 和 AutoZOOM 需要的查询次数少得多。

评估不同网络（图 4）。 为了验证我们的攻击对不同模型架构的鲁棒性，我们额外评估了 SimBA 和 SimBA-DCT 在 DenseNet-121 (Huang et al., ) 和 Inception v3 (Szegedy et al., 2016) 网络上的效果。图 4 显示了针对三种不同网络架构进行非定向攻击时，成功率相对于模型查询次数的变化。ResNet-50 和 DenseNet-121 对我们的攻击表现出相似程度的脆弱性。然而，Inception v3 明显更难攻击，对于某些图像需要超过$10,000$ 次查询才能成功攻击。尽管如此，两种方法都能以高概率成功构建针对所有模型的对抗扰动。

定性结果（图 5）。 为了对我们的方法进行定性评估，我们展示了在非定向攻击进行对抗扰动之前和之后的几张随机选择的图像。为了比较，我们使用 QL 攻击攻击同一组图像。图 5 显示了干净图像和扰动后的图像，以及扰动 $L_2$-范数和查询次数。虽然所有攻击在改变标签方面都非常成功，但 SimBA 和 SimBA-DCT 构建的对抗扰动的范数远小于 QL 攻击。对于几乎所有图像，两种方法所需的查询次数都持续少于 QL 攻击。事实上，SimBA-DCT 能够用少至 36 次模型查询就找到一个对抗样本！请注意，SimBA 产生的扰动包含稀疏但尖锐的差异，构成低 $L_0$-范数攻击。SimBA-DCT 产生在频率空间中稀疏的扰动，由此导致的像素空间变化分布到所有像素上。

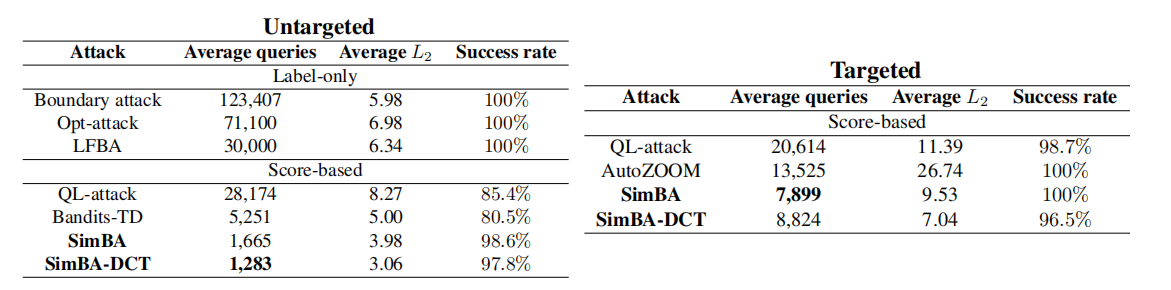
表 1: ImageNet 上非定向（左）和定向（右）攻击的平均查询次数表。方法在三个不同指标上进行评估：成功前的平均查询次数（越低越好），平均扰动 $L_2$-范数（越低越好），成功率（越高越好）。SimBA 和 SimBA-DCT 都实现了接近 $100\%$ 的成功率，与比较中的其他方法相似，但需要显著更少的模型查询次数，同时实现了更低（lower）的平均$L_2$ 失真。

4.3 Google Cloud Vision 攻击

为了证明我们的攻击对现实世界系统的有效性，我们攻击了 Google Cloud Vision API，这是一个为任意输入图像提供标签的在线机器学习服务。对于给定的图像，API 返回图像中包含的顶部概念（top concepts）列表及其相关概率。由于无法获得与每个标签相关的完整概率列表，我们定义了一个非定向攻击，旨在移除原始图像中的前 3 个概念。我们使用原始前 3 个概念返回概率的最大值作为对抗损失，并使用 SimBA 来最小化这个损失。图 7 显示了一次攻击前后的样本图像。原始图像（左）包含与相机仪器相关的概念。SimBA 成功地将顶部概念替换为与武器相关的物体，而对原始图像的改变人眼无法察觉。补充材料中包含更多样本。

由于我们的攻击可以高效执行，我们评估了其在 50 张随机图像聚合上的有效性。对于 LFBA 基线，如果产生的扰动的 $L_2$-范数不超过我们攻击成功运行中的最高 $L_2$-范数，我们就定义攻击成功。图 6 显示了两种攻击在不同查询次数下的平均成功率。SimBA 在仅 5000 次 API 调用后就达到了 $70\%$ 的最终成功率，而 LFBA 在相同查询预算下只能成功 $25\%$。据我们所知，这是第一个在 Google Cloud Vision 上报告的高成功率对抗攻击结果，且查询次数非常有限。

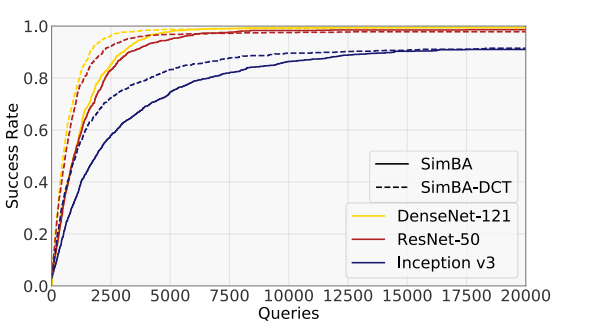
图 4: 不同网络架构下，非定向 SimBA（实线）和 SimBA-DCT（虚线）攻击的成功率与模型查询次数的比较。两种方法都能以高概率在 $20,000$ 次查询内成功构建对抗扰动。DenseNet 对两种攻击最脆弱，SimBA 仅需 $6,000$ 次查询，SimBA-DCT 仅需 $4,000$ 次查询后成功率就接近 $100\%$。Inception v3 对两种方法来说都更难攻击。

图 5: 随机选择的图像在 SimBA、SimBA-DCT 和 QL 攻击进行对抗扰动前后的效果。对于所有三种方法，构建的扰动都是人眼无法察觉的，但在所有图像上，SimBA 和 SimBA-DCT 的扰动 $L_2$-范数都显著低于 QL 攻击。我们的方法能够以与 QL 攻击相当或更少的查询次数构建对抗样本——在某些情况下少至 36 次查询！放大查看细节。

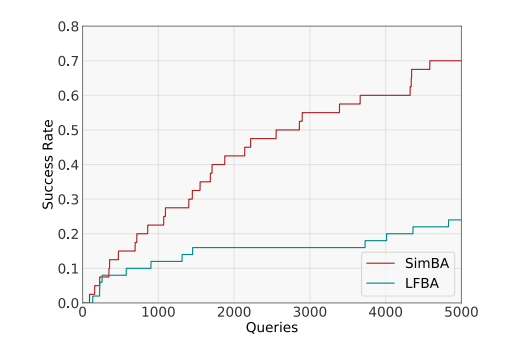
图 6: Google Cloud Vision 攻击的成功率与模型查询次数的关系图。SimBA 在仅 5000 次查询后就能达到接近 $70\%$ 的成功率，而 LFBA 的成功率仅达到$25\%$。

5 相关工作

许多近期研究表明，白盒和黑盒攻击都可以应用于多种任务。

用于图像分割（image segmentation）和物体检测（object detection）的计算机视觉模型也已被证明容易受到对抗扰动的影响 (Cisse et al., ; Xie et al., 2017)。Carlini & Wagner (2018) 对语音识别攻击进行了系统研究，表明可以构建鲁棒的对抗样本来改变转录模型以输出任意目标短语。对神经网络策略（neural network policies）的攻击 (Huang et al., ; Behzadan & Munir, 2017) 也已被证明是可行的。

随着这些攻击的普及，许多近期工作致力于设计针对对抗样本的防御措施。一类常见的防御在分类前应用图像变换（image transformation），旨在在不改变图像内容的情况下去除对抗扰动 (Xu et al., 2017; Dziugaite et al., 2016; Guo et al., 2017)。另一种策略不是要求模型正确分类所有对抗图像，而是检测攻击并在输入的某些统计量出现异常时输出一个对抗类别（adversarial class）(Li & Li, 2017; Metzen et al., 2017; Meng & Chen, 2017; Lu et al., 2017)。训练过程也可以通过将对抗损失作为隐式或显式正则化项（regularizer）纳入进来进行加强，以提高对对抗扰动的鲁棒性 (Tramer et al., 2017; Madry et al., 2017; Cisse et al., )。虽然这些防御在面对被动对手（passive adversary）时显示出巨大成功，但几乎所有防御都可以通过修改攻击策略轻松击败 (Carlini & Wagner, ; Athalye & Carlini, 2018; Athalye et al., 2018)。

相对于针对白盒攻击的防御，很少有研究关注防御可能仅通过黑盒查询访问模型的对手。虽然迁移攻击（transfer attacks）可以通过集成对抗训练（ensemble adversarial training）(Tramer et al., 2017) 和图像变换 (Guo et al., 2017) 等方法有效缓解，但尚不清楚现有的防御策略是否可以应用于可能通过查询访问模型的自适应对手（adaptive adversaries）。Guo et al. (2018) 表明边界攻击容易受到量化决策边界的图像变换的影响，但在低频空间中进行攻击可以成功规避这些变换防御。

6 讨论与结论

我们提出了 SimBA，一种简单的黑盒对抗攻击，它在连续值模型输出的迭代引导下采取小步长。我们方法前所未有的查询效率为未来黑盒对抗样本的研究建立了一个强大的基线。鉴于其在现实世界中的适用性，我们希望更多的努力可以投入到在这种更现实的威胁模型下防御恶意对手。

虽然我们有意避免使用更复杂的技术来改进 SimBA 以保持简单性，但我们相信额外的修改仍然可以显著减少模型查询次数。一个可能的扩展是进一步研究不同标准正交基集合的选择，通过增加找到大变化方向（direction of large change）的概率，这对我们方法的效率至关重要。另一个可以改进的领域是步长 $ϵ$ 的自适应选择，以最优地消耗距离和查询预算。

鉴于我们的方法要求非常少，它在概念上适用于目标模型为预测返回连续分数的任何任务。例如，语音识别系统被训练以最大化正确转录的概率 (Amodei et al., 2016)，策略网络（policy networks）(Mnih et al., 2015) 被训练以在给定当前环境条件下最大化动作集合上的某个奖励函数（reward function）。一种随机修改输入的简单迭代算法可能在这些场景中被证明是有效的。我们将这些方向留给未来的工作。

图 7: Google Cloud Vision 对样本图像在对抗扰动前后的标记结果截图。原始图像包含一组相机仪器。对抗图像成功地将顶部概念替换为枪支和武器。更多样本见补充材料。