题目描述

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 严格小于 当前节点的数。
节点的右子树只包含 严格大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

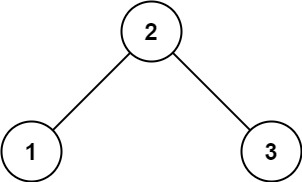
输入：root = [2,1,3]
输出：true

示例 2：

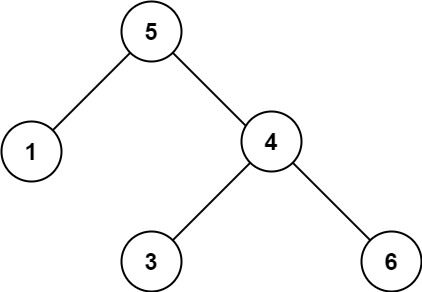
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。

提示：
树中节点数目范围在$[1,10^4]$ 内
$-2^{3}1<=Node.val<=2^{3}1-1$

思考一：前序遍历（递归检测值范围）

二叉搜索树的根节点的值大于所有左子树的节点，小于所有右子树的节点。写递归函数时很容易把节点值的范围搞错，如下图不是二叉搜索树：

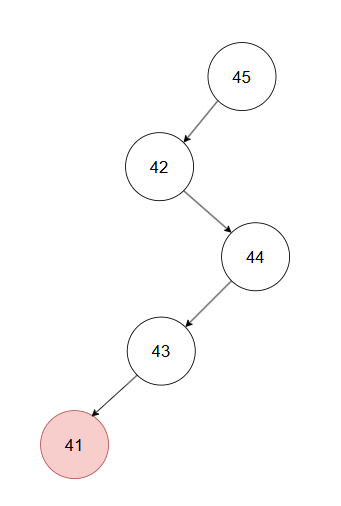
节点41 小于祖先节点42，不满足二叉搜索树根节点右子树所有节点大于根节点值条件。
因此要定义一个递归函数，设置上下限参数，检测左子树时才更新上限值，检测右子树时才更新下限值。
核心是为每个节点设定合法值区间：根节点的合法区间为 (-∞, +∞)，左子节点的区间上限更新为父节点值（需严格小于父节点），右子节点的区间下限更新为父节点值（需严格大于父节点），递归验证所有节点是否在合法区间内。

算法过程

1. 初始化递归：调用辅助函数 check，传入根节点及初始区间 (-Infinity, Infinity)（根节点无上下限约束）。
2. 递归终止条件：若当前节点为 null（空树/空子树），符合BST规则，返回 true。
3. 节点值合法性检测：
   • 若当前节点值 <= 区间下限 或 >= 区间上限（违反“左小右大”规则），返回 false。
4. 递归验证子树：
   • 验证左子树：左子树的合法区间为 (原下限, 当前节点值)（左子树需严格小于当前节点）；
   • 验证右子树：右子树的合法区间为 (当前节点值, 原上限)（右子树需严格大于当前节点）；
   • 只有左右子树均验证通过，才返回 true。
5. 返回结果：递归回溯后，返回最终验证结果。

时空复杂度

• 时间复杂度：O(n)，n为二叉树节点总数。
  原因：每个节点仅被验证1次，递归操作无重复遍历，总操作次数与节点数线性相关。
• 空间复杂度：O(h)，h为二叉树高度。
  原因：递归调用栈深度取决于树高，平衡树h=O(log n)，链状树h=O(n)。

代码（前序遍历版）

/*** Definition for a binary tree node.* function TreeNode(val, left, right) {*     this.val = (val===undefined ? 0 : val)*     this.left = (left===undefined ? null : left)*     this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @return {boolean}*/
var isValidBST = function(root) {// 初始区间：根节点无上下限，用正负无穷表示return check(root, -Infinity, Infinity);
};// 辅助函数：验证节点是否在 [low, high) 区间内（左闭右开，保证严格大小）
function check(node, low, high) {// 空节点符合BST规则if (!node) return true;// 节点值超出合法区间，不是BSTif (node.val <= low || node.val >= high) {return false;}// 左子树区间更新为 [low, node.val)，右子树更新为 [node.val, high)return check(node.left, low, node.val) && check(node.right, node.val, high);
}

思考二：中序遍历（验证序列严格递增）

核心是利用BST的中序遍历特性：BST的中序遍历结果是严格递增的序列（左→根→右，值依次增大）。通过中序遍历收集节点值，再检查序列是否严格递增，即可验证是否为有效BST。

算法过程

1. 中序遍历收集节点值：
   • 初始化空数组 arr，用于存储中序遍历的节点值；
   • 递归执行中序遍历：先遍历左子树，再将当前节点值加入 arr，最后遍历右子树（左→根→右）。
2. 验证序列严格递增：
   • 遍历数组 arr，若存在任意 i 满足 arr[i] >= arr[i+1]（非严格递增），返回 false；
   • 若所有相邻元素均满足 arr[i] < arr[i+1]，返回 true。
3. 返回结果：返回序列验证结果。

时空复杂度

• 时间复杂度：O(n)，n为二叉树节点总数。
  原因：中序遍历收集节点值需O(n)，遍历数组验证需O(n)，总时间为O(n)。
• 空间复杂度：O(n)（含存储数组）。
  原因：数组 arr 需存储所有节点值（O(n)），递归调用栈需O(h)，总空间由数组主导，为O(n)。
  （优化：可不用数组，用变量记录前一个节点值，空间复杂度降至O(h)，见下方补充）

代码（中序遍历版，基础版）

/*** Definition for a binary tree node.* function TreeNode(val, left, right) {*     this.val = (val===undefined ? 0 : val)*     this.left = (left===undefined ? null : left)*     this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @return {boolean}*/
var isValidBST = function(root) {const arr = [];// 中序遍历收集节点值inOrder(root, arr);// 验证序列是否严格递增for (let i = 0; i < arr.length - 1; i++) {if (arr[i] >= arr[i + 1]) return false;}    return true;
};// 中序遍历：左→根→右
function inOrder(node, arr) {if (!node) return;inOrder(node.left, arr);arr.push(node.val);inOrder(node.right, arr);
}

中序遍历优化版（无数组，O(h)空间）

var isValidBST = function(root) {let prev = -Infinity; // 记录前一个节点值，初始为负无穷let isValid = true;   // 标记是否为有效BSTfunction inOrder(node) {if (!node || !isValid) return; // 提前终止（已判定无效）inOrder(node.left);            // 左// 验证当前节点值是否大于前一个节点值if (node.val <= prev) {isValid = false;return;}prev = node.val;               // 更新前一个节点值（根）inOrder(node.right);           // 右}inOrder(root);return isValid;
};

两种方法对比

方法	核心逻辑	时间复杂度	空间复杂度（基础版）	优势
前序遍历（值范围）	递归验证节点合法区间	O(n)	O(h)	无额外存储，空间更优
中序遍历（有序性）	验证中序序列严格递增	O(n)	O(n)（数组）	逻辑直观，易理解
中序遍历（优化版）	实时对比前节点值	O(n)	O(h)	兼顾直观与空间效率

适用场景：

• 若追求空间效率，优先选择“前序遍历（值范围）”或“中序遍历优化版”；
• 若追求代码简洁直观，可选择“中序遍历（数组版）”（节点数较少时无明显性能问题）。