单纯形法的原理

先来举个例子：
用单纯形法求解下面线性规划问题的最优解：

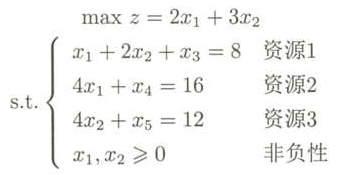
注释：解的过程是反复迭代的过程，如果第一次迭代没有理解也没关系，再继续看第二次迭代，和第三次迭代，每次迭代的流程都是一样的，建议自己看完之后，再手写一遍回忆一下哦~~

解析：

单纯形法的原理

线性规划问题的标准型如图：

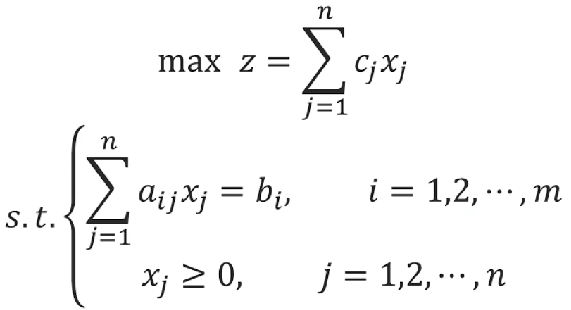
首先要得到一个初始的基可行解，具体做法如下：

假设系数矩阵A为下图所示的情形：

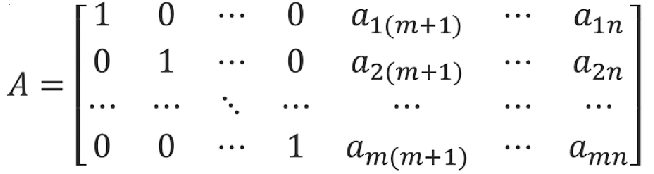
它的前m列就可以组成一个满秩矩阵B，且有B=（P₁,P₂······P_m）=I
再将基变量用非基变量来表示：

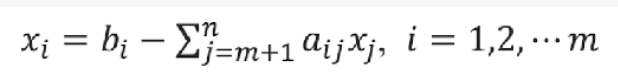
此时的目标函数里面的基变量也用非基变量表示：

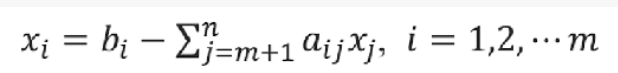
此时，令非基变量全部为0，就可以得到一个初始的基可行解：

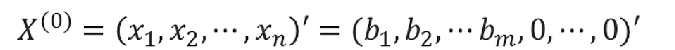
第二步就是判断得到的基可行解是否是最优解，具体做法如下：

目标函数在此时就变为只含非基变量的形式：

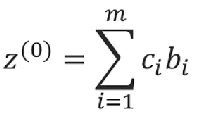
观察目标函数中非基变量的系数:

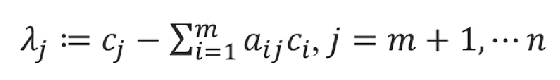
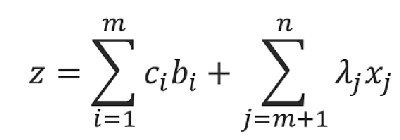
如果从λ_m+1一直到λ_n中只要有一个系数是正的，那么就说明当前的基可行解不是最优解，需要进一步改进目标函数的值，只有一直改到所有非基变量的系数全部为负时才说明那个时刻的基可行解是最优解。
因为用λ_i来判断最优解的情况，所以λ_i就被称为是检验系数。

第三步的改进就是更改基变量，然后迭代出新的目标函数，得到新的基可行解。具体的方法仍然是先比较目标函数中非基变量中的系数，选择系数最大的变量作为入基，然后接着上述步骤来继续进行迭代改变目标函数。
单纯形法的基本步骤总结：

定理1

对基可行解，如所有的检验系数λ_k≤0，k=m+1······n,那么X^(0)就是线性规划问题的最优解。
因为只有非基变量都是≤0的情况时，此时Z才能获得最大值。
（如果随以上步骤理解的话，这个定理就很明显了。
）

定理2

若某一个非基变量x_k的检验系数为正，对应的列向量P_k=（a_1k,a_2k,······a_mk）所有的元素为非正，那么线性规划问题就没有最优解。

这个定理可以来判断无界解。

单纯形表

单纯形表的布局方式：

具体的计算步骤如下：

举个例子：
就以这篇文章开头的例子为题，用单纯形表来解的步骤如下：

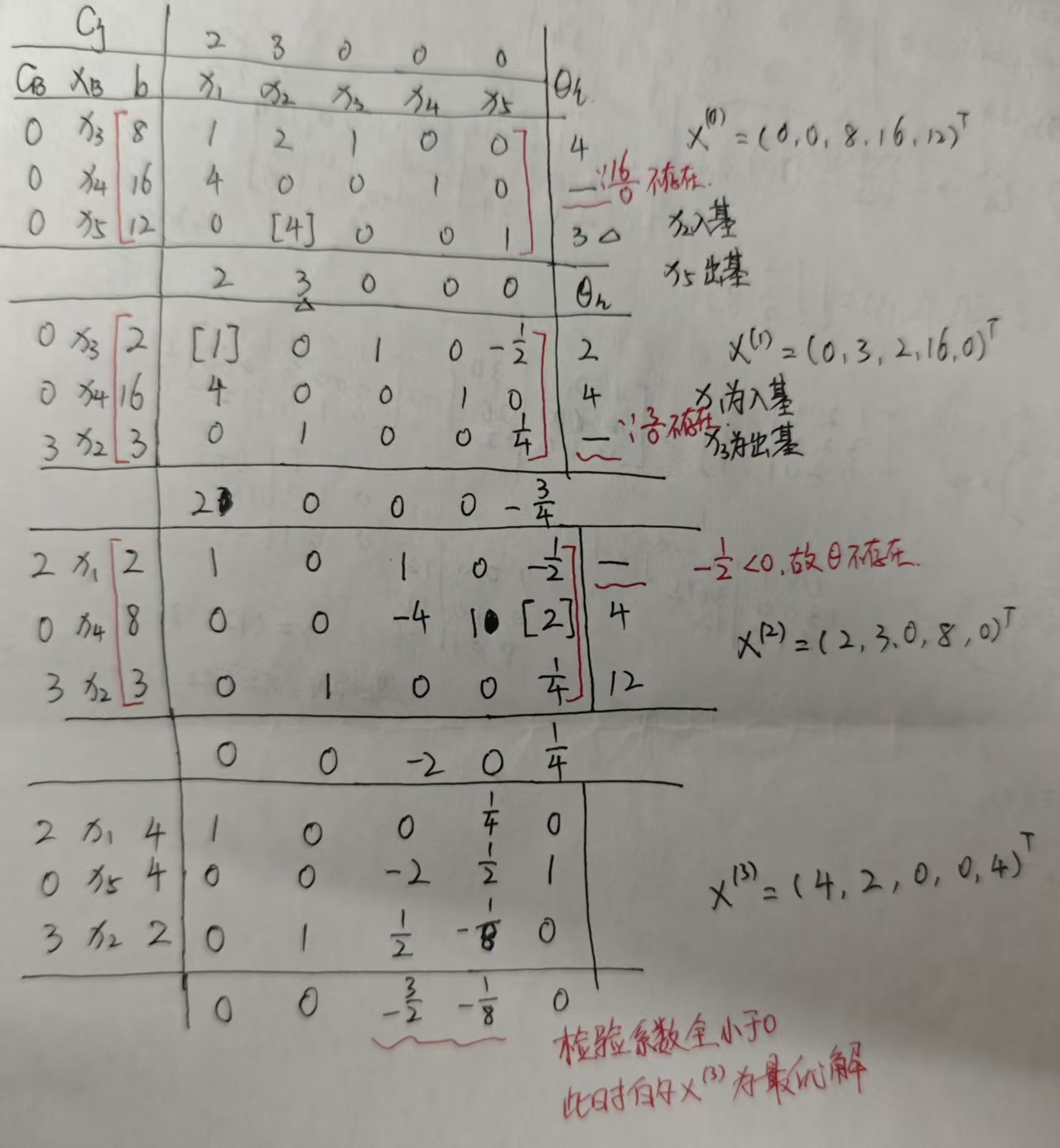
在第一个表中，只是将初始的全部数据列出，需要计算的是最后一行检验系数和最后一列Θ_i的值.x₁所在列对应的检验值由公式：μ_i=c_i - ∑c_jx_i可得μ₁=2 -（01+04+00）=2，那么x₂所在列对应的检验值由公式就可得μ₂=3 -（02+04+0*4）=3，选出最大的项是x₂对应的3。
再计算最后一列Θ_i的值，第一行Θ_i的值：8➗2=4，第二行Θ_i的值：16➗0是不存在的，所以画一条横线，第三行Θ_i的值：12➗4=3，选取Θ_i的值最小的数为3，所以具体就对应到中间系数矩阵的第三行，第二列的数值4，说明x₂为入基，x₄为出基，此时将4所在位置的这一列化为单位向量，也就是这一列化成（0,0,1）^T的形式。一定要以增广矩阵为整体来做初等行变换。
一直到所有的检验系数都是负数时停止换基迭代，此时对应的z值就是：z=∑c_i✖️b。
每一步对应的基不同时，一定要记得变换，基的确定是在对增广矩阵做初等行变换后才确定的