目录
1.程序功能描述
2.测试软件版本以及运行结果展示
3.部分程序
4.算法理论概述
5.完整程序
1.程序功能描述
在压印过程中,一般情况下,我们遵循质量,动量和能量守恒的原则进行仿真。然后建立偏微分方程组,然后通过有限元的方法,将方程离散化,然后进行求解,得到最后的结果。
2.测试软件版本以及运行结果展示
MATLAB2022A/MATLAB2024B版本运行
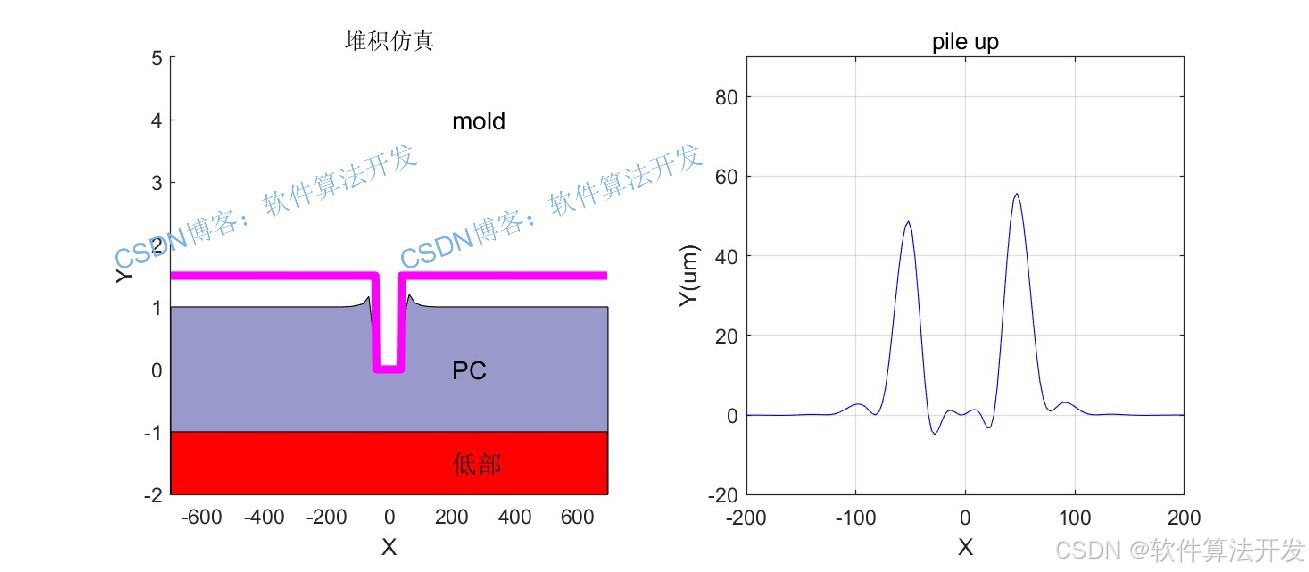
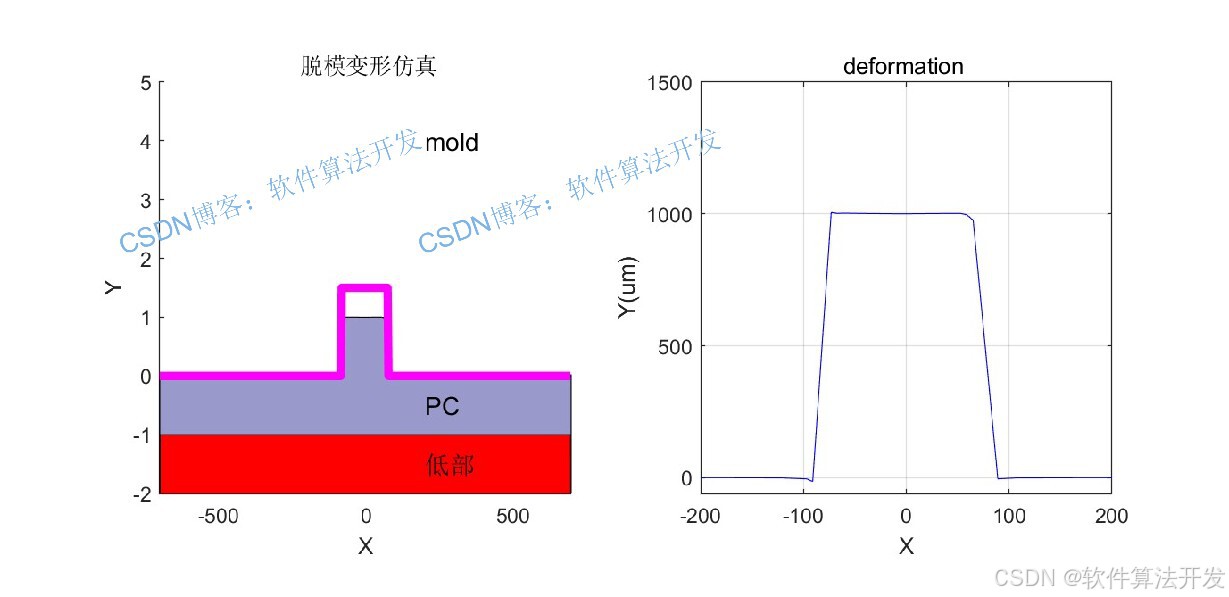
3.部分程序
%参数初始化
Mold_Move_Set = [0:5:75];
latitude = 100000;
Fliud_Thick_Thin = 10;
delrho = 2;
Width_Pitch = 50;
Scale = 50;
Alphas = 999;
H = Fliud_Thick_Thin;
g = 9.8;
delr = delrho/1000.;
c = sqrt(delr*g*H);
Ks = 8.64e4;
%主函数
f = func_glasswave(latitude);
%变形半径
Radius_dem = c/abs(f+1e-20);
W = Width_Pitch/Radius_dem;
Scale2 = abs(Scale);
[coffg1,coffg2] = func_coff(g,delr,Scale2,f,Radius_dem,H,c);
Mach = coffg2/c;
dx = 3e3;
Lmax = 700e3;
Lmin = 500e3;
x_array =-Lmax:dx:Lmax;
Len_x_array = length(x_array);
N1 = round((Lmax - Lmin)/dx);
N2 = Len_x_array - round((Lmax - Lmin)/dx);
Ldindex = func_wind(Len_x_array,N1,N2);
Decays = (1./(Alphas*Ks));
%偏微分方程的有限元分割步进
FEM_Step = 0.1;
dt = FEM_Step*dx/c;
Nsteps = round(0.2*Ks/dt);
%数值仿真分割数
K = 40;
Kd = sqrt(K*0.2*Ks)/1000;
NonLinear1 = 1;
NonLinear2 = 1;
[m,nu] = size(x_array);
xh = ones(1,nu-1);
xh = cumsum(xh)*dx;
nh = nu - 1;.................................
034_001m1
4.算法理论概述
第一种结构如下所示:
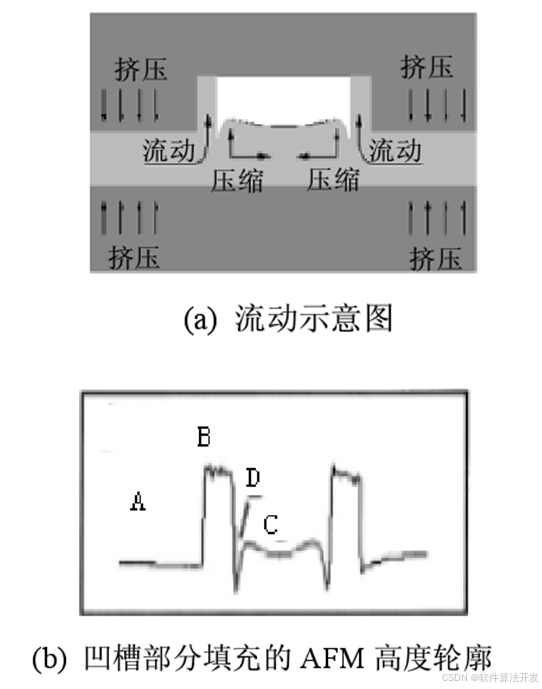
即聚合物的横向(从周边)粘性流动。对于图(a)的只有一个凹槽结构的简单模板压印情形,模板凸区下的聚合物受到强烈挤压而流入相邻两个凸区之间的空腔中,并沿着空腔侧壁上升,而空腔内原有的聚合物由于受到两侧流体的挤压,会向上凸起变形,两股流体不能融合为一体,因而在交界处形成凹性接点。随着压印时间的延长,两侧聚合物不断向空腔内挤压,原有的聚合物不断压缩上升,最后整个空腔被填满。
第二种结构如下所示:
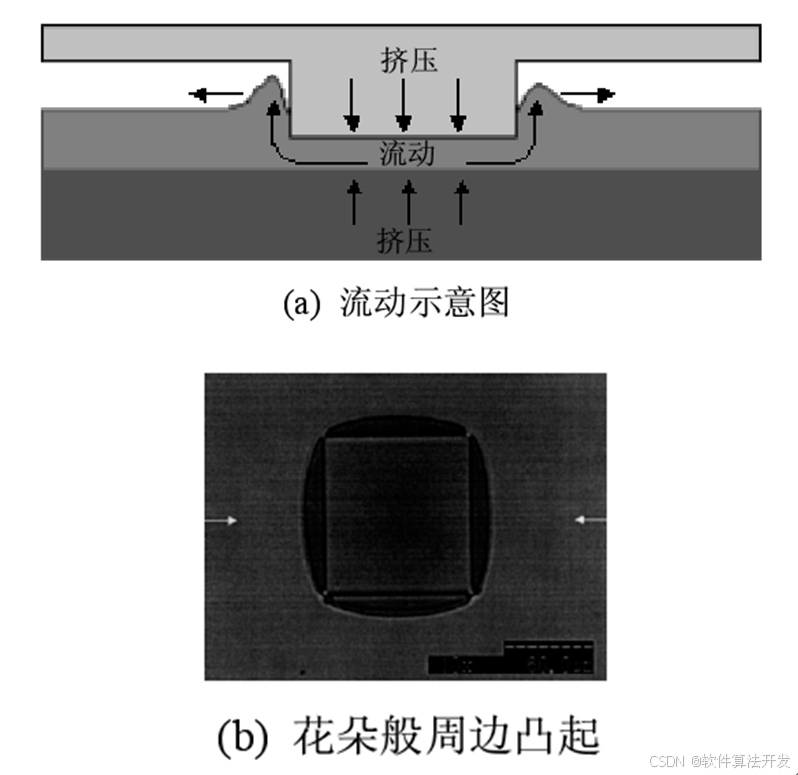
对于图 (a)只有一个凸起结构的模板压印情形,凸模下方的聚合物受到压挤而向周边流动,由于被挤出的聚合物与周边聚合物相比,数量较少,难以顺畅推动周边聚合物,因而在两股流体的汇合处形成类型花朵的突起。
纳米压印开始时,聚合物流动一般表现为横向粘性流动,如果聚合物薄膜各处力学性能或温差或压力等存在较大差异,尤其是当聚合物膜较薄和压力又较大时,聚合物便会从薄膜表面上隆起。
隆起密度和高度与聚合物薄膜性能的一致性程度和具体压印条件有关。隆起产生后,与聚合物的横向粘性流动交替作用,使得填充压模空腔中的聚合物不断从横向和纵向两个方向扩展直至充满整个空腔。
上述纳米压印聚合物的流动机理对于优化压印工艺条件和模板设计具有重要意义。当模板尺寸较小,且凸区和凹区结构尺寸相近时,聚合物一般以简单流动机理填充空腔,容易充分填满空腔;当凹区结构尺寸与凸区相比相对较大,尤其是空腔的深宽比又较大时,聚合物转移相对困难,易产生纵向隆起,需要较大的压力或较高的压印温度或较厚的聚合物薄膜;当模板尺寸较大时,且凸区和凹区结构尺寸相近的图形结构,如果能保持各处的压力和温度的一致性,聚合物也较容易充分转移;但如果模板周边具有大量的空白区域,尤其是当空腔深宽比又较大时,由于聚合物的流动主要来自周边,各空腔填空次序不一,越靠近中心的空腔越不易填充,此时需要较大的压力或较高的压印温度或较大压印深度。
上述的过程,简单的讲,就是这么两个过程:
向凹入的间隙中填冲;
被突出的模板挤向两边;
然后,我们的模型,就是上述过程的周期性运动:
上述两种情况,在本质上,其数学模型是类似的,这里进行详细的介绍和说明:
在宏观领域,基于任意的拉格朗日—欧拉方法(ALE)的流体动力学方程被用来处理复杂的流固耦合过程。一般在固体力学中,习惯采用Lagrange坐标系;而流体力学中更多地使用Euler坐标系。这样可以使计算网格不再确定,也不依附于流体质点,而可以相对于坐标架做任意运动,以实现网格的不断更新而不致发生畸变。
建模的时候,遵循质量,动量,能量守恒原则。
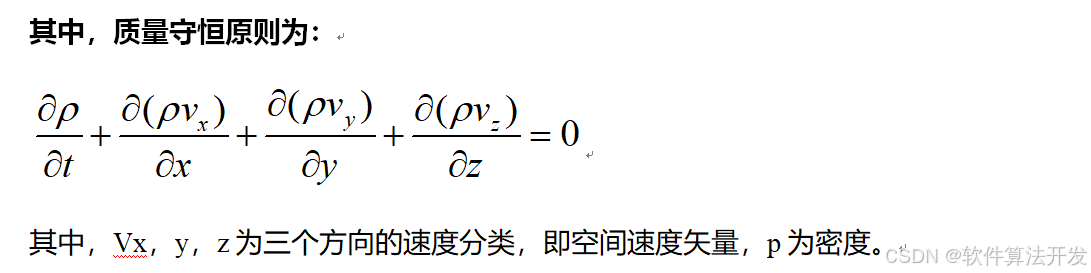
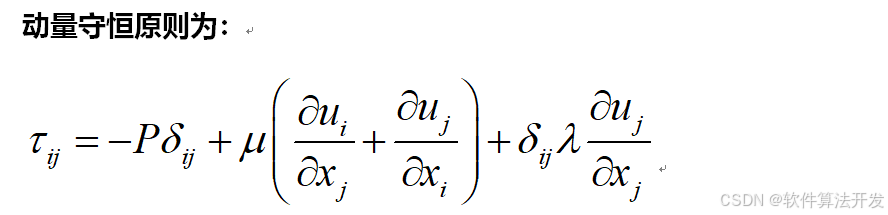


5.完整程序
VVV
)

![【线性代数基础 | 那忘算9】基尔霍夫(拉普拉斯)矩阵 矩阵—树定理证明 [详细推导]](http://pic.xiahunao.cn/【线性代数基础 | 那忘算9】基尔霍夫(拉普拉斯)矩阵 矩阵—树定理证明 [详细推导])

)








)





