有限马尔可夫决策过程

基本概念

多臂老虎机仅涉及评价性反馈，即动作的即时奖励，估计每个动作 $a$ 的价值 $q_{\ast }(a)$。

有限马尔可夫决策过程（Finite MDP）引入了关联性因素，即在不同状态（情境）下选择不同动作，动作不仅影响即时奖励，还通过改变环境状态影响未来的奖励，因此涉及延迟奖励以及长期与短期奖励之间的权衡。是强化学习中序贯决策问题的经典数学建模方式，扩展了多臂老虎机问题。在MDP中需要更精细的价值估计：

• 在状态 $ s $ 下动作 $ a $ 的最优价值：
  $$q_{\ast }(s,a)$$

• 状态 $ s $ 的最优价值（在最优策略下）：
  $$v_{\ast }(s)$$

这些状态相关的价值函数是将长期后果归因于具体动作选择的关键工具。

智能体-环境交互接口

实体	定义
智能体（Agent）	学习和决策的主体
环境（Environment）	智能体之外的一切，对动作做出响应

智能体选择动作，环境对这些动作做出响应，并向智能体呈现新的情境。环境还会产生奖励，智能体的目标就是通过选择动作，从长远来看最大化所获得的奖励总量。

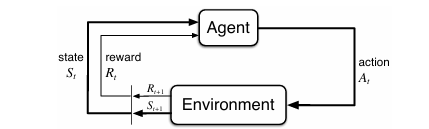
图3.1：马尔可夫决策过程中智能体与环境的交互。

交互流程

在离散的时间步$ t = 0, 1, 2, \dots $内，智能体与环境持续交互，每个时间步发生以下事件序列：
$$S_t\stackrel{\text{agent}}{\to }{A}_t\stackrel{\text{environment}}{\to }{R}_{t+1},S_{t+1}$$

即：

1. 智能体观察当前状态 $ S_t \in \mathcal{S} $
2. 选择动作 $ A_t \in \mathcal{A}(s) $
3. 环境响应：
   • 给出奖励 $ R_{t+1} \in \mathcal{R} \subset \mathbb{R} $
   • 进入新状态 $ S_{t+1} $

整个交互过程形成一个序列，称为轨迹：

$$S_0,A_0,R_1,S_1,A_1,R_2,S_2,A_2,R_3,\dots \text{\hspace{1em}(3.1)}$$

有限MDP

状态集 $ \mathcal{S} $、动作集 $ \mathcal{A} $、奖励集 $ \mathcal{R} $：有限个可能取值都只有有限个元素。

随机变量 $R_t$ 和 $S_t$ 具有明确定义的离散概率分布，且这些分布仅依赖于前一个状态和动作。

对于这些随机变量的特定取值 $s^{\prime }\in \mathcal{S}$ 和 $r\in \mathcal{R}$，在给定前一个状态 $s$ 和动作 $a$ 的条件下，它们在时间 $t$ 出现的概率为：
p(s′,r∣s,a)≐Pr⁡{St=s′,Rt=r∣St−1=s,At−1=a}(3.2) p(s', r | s, a) \doteq \Pr\{S_t = s', R_t = r \mid S_{t-1} = s, A_{t-1} = a\} \tag{3.2} p(s′,r∣s,a)≐Pr{St​=s′,Rt​=r∣St−1​=s,At−1​=a}(3.2)

[!NOTE]

符号 $ \doteq $ 表示“定义为”

同时有

$$\sum _{s^{\prime }\in \mathcal{S}}\sum _{r\in \mathcal{R}}p(s^{\prime },r|s,a)=1,\forall s\in \mathcal{S},a\in \mathcal{A}(s)\text{\hspace{1em}(3.3)}$$

在马尔可夫决策过程中，条件概率 $ p(s’, r|s, a) $ 决定了所有未来动态。$ S_t $ 和 $ R_t $ 的分布仅依赖于前一状态 $ S_{t-1} $ 和动作 $ A_{t-1} $，与更早的历史无关。这要求状态必须包含所有对未来有影响的信息。马尔可夫性质是对“状态”的限制，而非过程本身；若状态满足此性质，则称其具有马尔可夫性。

相关计算量

状态转移概率

p(s′∣s,a)≐Pr⁡{St=s′∣St−1=s,At−1=a}=∑r∈Rp(s′,r∣s,a)(3.4) p(s'|s,a) \doteq \Pr\{S_t = s' \mid S_{t-1} = s, A_{t-1} = a\} = \sum_{r \in \mathcal{R}} p(s', r|s, a) \tag{3.4} p(s′∣s,a)≐Pr{St​=s′∣St−1​=s,At−1​=a}=r∈R∑​p(s′,r∣s,a)(3.4)

状态-动作对的期望奖励

$$r(s,a)\doteq \mathbb{E}[R_t\mid S_{t-1}=s,A_{t-1}=a]=\sum _{r\in \mathcal{R}}r\sum _{s^{\prime }\in \mathcal{S}}p(s^{\prime },r|s,a)\text{\hspace{1em}(3.5)}$$

给定下一状态的期望奖励

$$r(s,a,s^{\prime })\doteq \mathbb{E}[R_t\mid S_{t-1}=s,A_{t-1}=a,S_t=s^{\prime }]=\sum _{r\in \mathcal{R}}r\cdot \frac{p(s^{\prime },r|s,a)}{p(s^{\prime }|s,a)}\text{\hspace{1em}(3.6)}$$

MDP框架

框架中时间步的含义不必对应真实时间间隔，可表示任意决策阶段的连续序列。

动作可以是：低层次控制信号（如电机电压）也可以是高层次决策（如“去吃午饭”）或者心理或计算性动作（如“集中注意力”、“思考某个问题”）。

状态可基于原始传感器数据、抽象符号描述（如物体位置）、记忆信息或者主观心理状态（如“不确定”、“惊讶”）。

智能体与环境

**任何不能被智能体任意改变的事物都属于环境。**同时并不假设智能体对环境一无所知，智能体-环境边界代表的是智能体绝对控制能力的极限，而非其知识的极限。 智能体可以了解环境机制，但不能随意更改任务目标。可根据任务需求设置不同边界，复杂系统中可存在多个智能体，各自有独立边界。高层智能体的输出可以成为低层智能体的状态输入。

MDP将学习目标导向行为的问题简化为三个核心信号的交互：

信号	含义
状态 $ S_t $	决策的基础（当前情境）
动作 $ A_t $	智能体的选择
奖励 $ R_t $	目标定义（标量数值）

状态和动作的具体表示方式极大影响性能，表示选择目前更多是艺术而非科学，后续的重点在表示确定后，学习行为的一般性原则。

实例分析

生物反应器

• 任务：控制温度和搅拌速率以最大化化学品产出
• 动作：目标温度、目标搅拌速率（向量）
• 状态：传感器读数 + 符号输入（原料/目标化学品）
• 奖励：单位时间产出速率（瞬时度量）

拾取-放置机器人

• 任务：实现快速、平滑的抓取放置
• 动作：施加到关节电机的电压
• 状态：关节角度和速度的实时读数
• 奖励：
  • 成功完成任务：+1
  • 每步根据“抖动”程度给予小负奖励（鼓励平滑）

回收机器人

• 办公室中移动机器人收集空苏打罐
• 配备传感器、机械臂、夹爪
• 电池供电，电量分为两种状态

状态空间

两种电量水平
S={high,low} \mathcal{S} = \{high, low\} S={high,low}

动作集

在每种状态下，智能体可以决定：(1) 主动搜索罐子一段时间，(2) 原地静止等待别人送来罐子，或 (3) 返回基地为电池充电。

• $ \mathcal{A}(high) = {search, wait} $
• $ \mathcal{A}(low) = {search, wait, recharge} $
  • 高电量时不提供充电选项（不合理）

奖励机制

• 收集一个罐子：+1
• 电池耗尽需救援：-3
• 其他时间：奖励为0
• 充电过程中无法收集罐子
• 耗尽电池的那一步也无法收集

转移动态

当前状态	动作	下一状态	转移概率	期望奖励
high	search	high	$ \alpha $	$ r_{\text{search}} $
high	search	low	$ 1-\alpha $	$ r_{\text{search}} $
high	wait	high	1	$ r_{\text{wait}} $
low	search	low	$ \beta $	$ r_{\text{search}} $
low	search	耗尽	$ 1-\beta $	-3（且无法收集）
low	wait	low	1	$ r_{\text{wait}} $
low	recharge	high	1	0（充电中无收益）

转移图表示法

• 图中两类节点：
  • 状态节点：大空心圆，标记状态名
  • 动作节点：小实心圆，标记动作名，连接至对应状态
• 流程：
  1. 从状态节点 $ s $ → 动作节点 $ (s,a) $
  2. 从动作节点发出箭头 → 下一状态节点 $ s’ $
• 每条箭头标注：
  • 转移概率 $ p(s’|s,a) $
  • 期望奖励 $ r(s,a,s’) $

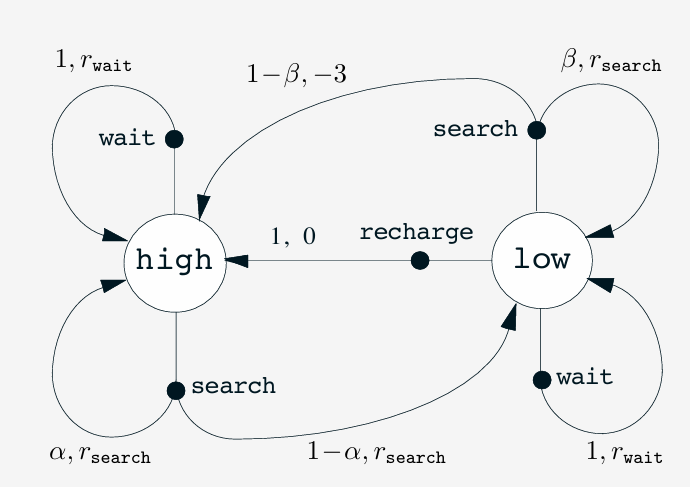
目标与奖励

在强化学习中，智能体的目标或目的通过一种特殊信号来形式化：奖励（Reward）奖励由环境传递给智能体，是一个标量数值$R_t\in \mathbb{R}$。每个时间步 $t$，环境根据当前状态转移和动作结果生成奖励 $R_t$智能体的目标不是最大化即时奖励，而是最大化长期累积奖励；更准确地说，是最大化未来奖励总和的期望值。

奖励假说

所有我们所说的“目标”和“目的”，都可以被很好地理解为：最大化一个接收到的标量信号（称为奖励）的累积和的期望值。

任何形式的目标（如行走、下棋、回收物品等），都可以通过设计合适的奖励信号来引导智能体实现。强化学习不预设“目标”的具体内容，而是将其完全交给奖励函数来定义。智能体本身并不“知道”任务目标，它只知道“要最大化奖励”。

尽管用单一数值表示目标看似受限，但实际上非常灵活且强大。

应用场景	奖励设计	目的
机器人走路	每步给予与前进速度成正比的奖励	学会高效前行
迷宫逃脱	每步给予 -1 的奖励，逃出后终止	鼓励尽快逃脱（最小化步数）
回收空罐	收集成功时 +1，其余时间 0	鼓励多收集罐子
安全行为	撞到物体或被呵斥时给予负奖励	鼓励避免危险或不当行为
下跳棋/国际象棋	获胜：+1，失败：-1，平局/中间状态：0	学会赢棋

智能体总是学习去最大化它的奖励，因此，设定的奖励必须真正反映出我们希望达成的目标。但奖励信号并不是用来向智能体传授“如何”实现目标的先验知识的地方，奖励信号是你向智能体传达“你想要它实现什么”的方式，而不是“你希望它如何实现”的方式。例如对于下棋智能体不应奖励吃掉对方棋子、控制棋盘中心等子目标，只应在游戏结束时根据胜负给予奖励。因为如果对“吃子”给予奖励，智能体可能学会牺牲大局去换取吃子机会；故意制造吃子局面，即使会导致最终输棋。

回报与回合

定义

智能体的目标是从长远来看最大化累积奖励。现在需要对回报进行数学定义。

令 $ R_{t+1}, R_{t+2}, R_{t+3}, \dots $ 表示从时间步 $ t+1 $ 开始的奖励序列。我们定义时间步 $ t $ 的回报 $ G_t $ 为这些奖励的某个函数。

最简单的情况，回报是所有奖励的总和：
Gt≐Rt+1+Rt+2+⋯+RT=∑k=1T−tRt+k=∑k=0∞Rt+k+1⋅1{t+k+1≤T}(3.7) G_t \doteq R_{t+1} + R_{t+2} + \cdots + R_T = \sum_{k=1}^{T-t} R_{t+k} = \sum_{k=0}^{\infty} R_{t+k+1} \cdot \mathbf{1}_{\{t+k+1 \leq T\}} \tag{3.7} Gt​≐Rt+1​+Rt+2​+⋯+RT​=k=1∑T−t​Rt+k​=k=0∑∞​Rt+k+1​⋅1{t+k+1≤T}​(3.7)

其中：

• $ T $：该回合的终止时间步（随机变量）
• 当 $ k > T - t $ 时，$ R_{t+k+1} = 0 $（已终止）

在存在自然终止状态的任务中，交互可划分为独立的回合。每个回合以终止状态结束，终止后系统重置至初始状态或初始状态分布。下一回合的开始与上一回合的结果无关。这类任务称为回合制任务，比如下棋等。

在回合制任务中，我们有时需要区分两个集合：

• $ \mathcal{S} $：所有非终止状态的集合
• $ \mathcal{S}^+ $：所有状态的集合，包括终止状态

持续性任务

持续性任务没有自然终止点，交互无限持续，如永不停止的机器人服务系统。此时不适用使用奖励综合定义汇报(任务的汇报会是无穷大)，因此使用折扣回报。

引入折扣率 $ \gamma \in [0, 1] $，定义：

$$G_t\doteq R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\cdots =\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1},\text{\hspace{1em}(3.8)}$$

越远的奖励被赋予越小的权重，$ R_{t+k+1} $ 的当前价值为 $ \gamma^k R_{t+k+1} $。

$ \gamma $ 值	含义
$ \gamma = 0 $	短视型（myopic）：只关心 $ R_{t+1} $，忽略未来
$ \gamma \to 1 $	远见型：高度重视长期奖励
$ 0 < \gamma < 1 $	平衡当前与未来奖励

[!IMPORTANT]

证明：

若 $ |R_k| \leq r_{\max} $（即奖励有界），且 $ \gamma < 1 $，则折扣回报
$$G_t=\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}$$
是收敛的，且其绝对值有界，即 $ |G_t| < \infty $

前提

奖励序列有界：存在常数 $ r_{\max} > 0 $，使得对所有 $ k $，都有
$$|R_{t+k+1}|\le r_{\max }$$
（例如：奖励总是在 $[-10,10]$ 之间）。折扣率满足：
$$0\le \gamma <1$$
由于 $ |R_{t+k+1}| \leq r_{\max} $，我们有：

$$|G_t|=\left|\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}\right|\le \sum _{k=0}^{\infty }\left|{\gamma }^k{R}_{t+k+1}\right|=\sum _{k=0}^{\infty }{\gamma }^k|R_{t+k+1}|$$

再利用 $ |R_{t+k+1}| \leq r_{\max} $，得到：

$$|G_t|\le \sum _{k=0}^{\infty }{\gamma }^k\cdot r_{\max }=r_{\max }\sum _{k=0}^{\infty }{\gamma }^k$$

我们知道，当 $ 0 \leq \gamma < 1 $ 时，几何级数收敛：

$$\sum _{k=0}^{\infty }{\gamma }^k=\frac{1}{1-\gamma }$$

所以：

$$|G_t|\le r_{\max }\cdot \frac{1}{1-\gamma }$$

这个上界是一个有限的正数（因为 $ \gamma < 1 $，分母不为零）。

因此，$ G_t $ 是绝对收敛的，且其值有限。

由公式 (3.8) 可得：

$$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+{\gamma }^3{R}_{t+4}+\cdots =R_{t+1}+\gamma (R_{t+2}+\gamma R_{t+3}+{\gamma }^2{R}_{t+4}+\cdots )=R_{t+1}+\gamma G_{t+1}\text{\hspace{1em}(3.9)}$$

这个式子 对所有 $ t < T $ 成立，只要定义 $ G_T = 0 $

若每步奖励为 +1，且 $ \gamma < 1 $，则：

$$G_t=\sum _{k=0}^{\infty }{\gamma }^k=\frac{1}{1-\gamma }\text{\hspace{1em}(3.10)}$$

案例

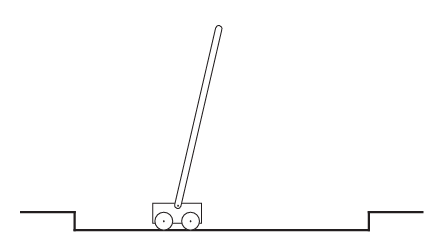
任务描述

对沿轨道移动的小车施加力，以保持铰接在小车上的杆不倒下。当杆偏离垂直方向超过某个角度，或小车跑出轨道时，视为失败。每次失败后，杆会被重置回垂直位置。

方案一：作为回合制任务

• 每步未失败 → 奖励 +1
• 失败时无额外奖励
• 回报 $ G_t = $ 直到失败前的剩余步数
• 最大化回报 ⇨ 尽可能延长平衡时间

方案二：作为持续性任务

• 失败时奖励 -1，其余时间 0
• 则 $ G_t = -\gamma^K $，其中 $ K $ 是距离下次失败的步数
• $ K $ 越大，$ \gamma^K $ 越小，$ -\gamma^K $ 越接近 0（更好）
• 所以仍鼓励延迟失败

统一记号

省略回合编号

在严格意义上，每个回合 $i$ 都有自己的时间步序列。因此应使用：

• $ S_{t,i}, A_{t,i}, R_{t,i} $：第 $i$ 个回合中时间步 $t$ 的状态、动作、奖励
• $ T_i $：第 $i$ 个回合的终止时间

但这会使表达变得复杂，

在实际讨论中，我们通常要么只关注某一个特定回合，要么陈述的是对所有回合都成立的结论。因此，我们可以轻微滥用记号，省略回合下标 $i$： 使用 $ S_t, A_t, R_t, T $ 等符号，隐含地表示“当前回合”的变量。

将终止视为“吸收状态”

将回合的终止看作进入一个特殊的吸收状态（absorbing state），满足一旦进入，永远停留（自循环）；每步产生零奖励；不再0有实际动作或状态变化.

例如假设一个回合有 3 步奖励：$ R_1 = +1, R_2 = +1, R_3 = +1 $，然后终止。

我们将其扩展为无限序列：

$$R_1=+1,R_2=+1,R_3=+1,R_4=0,R_5=0,R_6=0,\dots$$

并定义状态转移图如下：

$$S_0\stackrel{+1}{\to }{S}_1\stackrel{+1}{\to }{S}_2\stackrel{+1}{\to }\boxed{\text{Absorbing State}}\stackrel{0}{\to }\boxed{\text{Absorbing State}}\stackrel{0}{\to }\cdots$$

现在，则可以统一使用折扣回报公式：

$$G_t\doteq \sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}\text{\hspace{1em}(3.8)}$$

在回合制任务中的效果：

• 当 $ t \geq T $（已终止），所有后续 $ R_{t+k+1} = 0 $

• 所以：
  $$G_t=\sum _{k=0}^{T-t-1}{\gamma }^k{R}_{t+k+1}+\sum _{k=T-t}^{\infty }{\gamma }^k\cdot 0=\sum _{k=0}^{T-t-1}{\gamma }^k{R}_{t+k+1}$$

• 若 $ \gamma = 1 $，则退化为原始的有限和：$ G_t = \sum_{k=t+1}^{T} R_k $

在持续性任务中的效果：

• 无需终止，直接使用无限折扣和
• 吸收状态不出现，或仅用于理论构造