前言

本文主要对智能驾驶规划技术相关知识进行初步探究和总结，以加深理解，及方便后续学习过程中查漏补缺。

分层规划策略

寻径

A*算法

概念

• 节点：网格化后的每一个最小单元
• 父节点：路径规划中用于回溯的节点
• 列表：需要不断的维护
  • 开放列表：用于存放待检测节点
  • 关闭列表：用于存放已检测节点
• 路径排序F：选择路径的依据F=G+H。找最小路径
  • G：从初始位置移动到待检测节点的开销
  • H：启发函数。即，每个待检测节点到终点的代价。

算法流程

• 建立列表：将初始位置加入开放列表，并检查与之相邻的8个节点，把其中可通行节点（除去障碍物和限行节点）加入到开放列表，并把初始位置设置为这8个节点的父节点，然后把初始位置从开放列表中删除，并将其加入关闭列表。
• 选择移动节点：计算所有开放列表中节点的F值，选择其中最小的作为移动节点。
• 计算最小消耗F=G+H：计算G时允许纵向（10）、横向（10）、斜向（14）移动；计算H时只允许纵向（10）和横向（10）移动，且不考虑障碍物（曼哈顿距离）。
• 更新列表：将选中的节点从开放列表中移除，并加入到关闭列表中，接着检查与之相邻的可通行节点，如果节点不在开放列表中则将他们加入开放列表，并指定选中节点为其父节点；如果节点已经在开放列表中，则检查经过选中节点后F值是否会变小，若是，则重新指定父节点，若否，则不进行任何操作。
• 选择移动节点：计算开放列表中所有节点的F值，选择其中最小的作为移动节点。
• 更新列表：（循环）
• 更新选中节点：（循环）
• 循环过程：重复更新列表和更新选中节点两个步骤，直至重点位置出现在开放列表中。
• 找到路径：从目标位置开始，沿着父节点指向，反向找回初始位置，即可得到路径。
• 示例
  

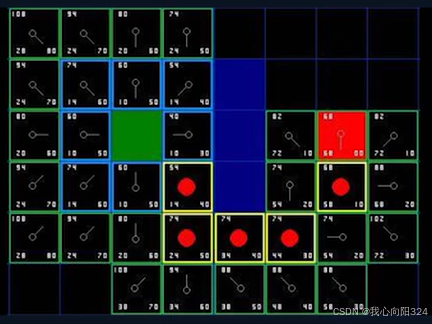
A*算法评价

• 全局最优的路径规划
• 对环境建模要求高，不仅要已知，还要网格化
• 环境越复杂，每个迭代过程中需要维护的开放列表会越大

车辆行为决策

输入

• 规划路径、驾驶情况（交通规则、路况）

输出

• 车辆行为（速度保持、前车跟随、减速停车、驻车、主动变道）

状态机建立

• 状态（每个状态对应一个车辆行为）
• 转变（从一个状态到另一个状态）
• 转变条件（状态发生转变需要符合的规则）
• 状态动作（车辆行为的约束）
• 示例
  

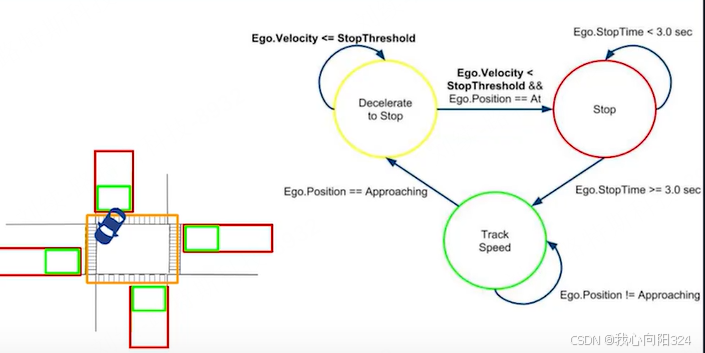
运动路径生成

局部运动路径生成

静态障碍物

快速扩展随机树方法（RRT）

• 随机树生长
  • 选择起点qs作为树的根节点，通过扩展叶节点的方式建立随机树。
  • 从随机树当前所有的叶节点中，选择一个距离qrand最近的节点，成为qnear，从qnear向qrand的方向延伸一个固定步长的距离，得到一个新的节点qnew，并以qnear为qnew的父节点，若qnew与障碍物发生冲突则放弃该节点，重复以上过程，直至qnew与目标距离足够小。
• 路径反向搜索
  • 以距离目标位置最近的叶节点为起始，依次向上搜索父节点，则可获得一条从起始位置到目标位置的可行路径。 （注：和A*算法类似）
• 伪代码
  
• RTT算法评价
  • 具有完备性
  • 计算量大，规划效率低
  • 规划路径不平滑

动态障碍物

人工势场法（APF）

• 势场中的物体受到引力势场和斥力势场的综合作用，向势能最低处运动。
• 势场的构建
  • 引力势场：势场大小与距离平方成正比，范围全局
  • 斥力势场：势场大小与距离平方成反比，范围局部
• 势场力（势场负梯度）
  • 引力：方向从物体指向目标点
  • 斥力：方向从障碍物指向物体
  • 合力：物体在合力作用下，实时生成路径
• APF算法评价
  • 在线规划，路径平滑
  • 只需考虑视野内的障碍物
  • 参数选择对效果影响较大
  • 会存在局部极小和徘徊现象