一、算法核心原理

RMSProp（Root Mean Square Propagation）是深度学习先驱Geoffrey Hinton在2012年提出的优化算法，它基于AdaGrad算法的改进，创新性地解决了传统梯度下降法中学习率固定不变的局限性。该算法的核心机制在于采用指数加权移动平均（EWMA，详情可参考连接：【深度学习】通俗易懂的基础知识：指数加权平均）方法，实现了对参数更新幅度的自适应动态调整。

二、RMSProp算法的公式推导

AdaGrad算法（【人工智能】神经网络的优化器optimizer（二）：Adagrad自适应学习率优化器）对于学习率的动态调整设计思路：把全部历史梯度一视同仁全部打包进行平方和，导致学习提早结束。

RMSProp算法对于学习率的动态调整设计思路：通过将Momentum动量优化器（【人工智能】神经网络的优化器optimizer（一）：Momentum动量优化器）中采用的指数加权平均（EWMA）应用到学习率动态调整中，以便于通过指数衰减将近期数据赋予高权重，历史数据逐渐“遗忘”，从而产生类似“滑动”的机制，避免学习率过早衰减的问题。

$v_{t}=\beta v_{t-1}+(1-\beta)x_{t}^{2}$

其中：

$v_{t}$ ：当前时刻的加权平均值
$v_{t-1}$ ：上一时刻的加权平均值（初始值 $v_{0}=0$ ）
$x_{t}$ ：想要观察的时刻 t 的值，在该文章中代表 t 时间的梯度
$\beta$ ：衰减因子（0<β<1），控制历史数据的权重分布‌

RMSProp为每个参数维护一个状态变量（通常记作 V），用于记录梯度平方的指数衰减平均值，剩下的其他公式就和AdaGrad算法是一样的了：

$\theta _{t+1}=\theta _{t}-\frac{\eta }{\sqrt{v_{t}+\epsilon }}\cdot x_{t}$

其算法的特点也和AdaGrad算法差不多：

‌分母设计‌： $v^{_{t}}$ 近似为梯度的均方根（Root Mean Square），反映历史梯度的幅值
‌自适应效果‌：
1. 梯度方向振荡剧烈（ $v^{_{t}}$ 较大）→ 学习率降低，抑制震荡
2. 梯度方向平缓（ $v^{_{t}}$ 较小）→ 学习率增大，加速收敛‌
稳定常数： $\varepsilon$ （如1e-8）用于数值稳定，防止分母为零‌

三、RMSProp算法和AdaGrad算法的对比

‌特性‌	‌RMSProp‌	‌AdaGrad‌
历史梯度累积方式	指数衰减加权平均	全局累积
学习率衰减趋势	动态平衡，避免过早趋近零	单调递减，后期更新停滞
适用场景	非平稳目标、深层网络、RNN‌	稀疏数据、浅层网络

根据上述内容可以总结出几个特点：

解决AdaGrad缺陷‌：AdaGrad累积所有历史梯度导致后期学习率过小，RMSProp通过衰减系数 γ 削弱早期梯度的影响，使学习率在训练中保持有效调整能力‌；
‌适应非平稳目标‌：在RNN等动态系统中，梯度分布随时间变化，RMSProp的指数衰减能更快响应近期变化‌；
‌超参数影响‌：γγ 过大易忽略新梯度信息，过小则退化为类似AdaGrad，通常取0.9经验值‌。

综上所述，RMSProp的衰减机制通过加权平均平衡历史与当前梯度，实现学习率的稳定自适应调整，显著提升非凸优化问题的训练效率‌。

四、代码实现

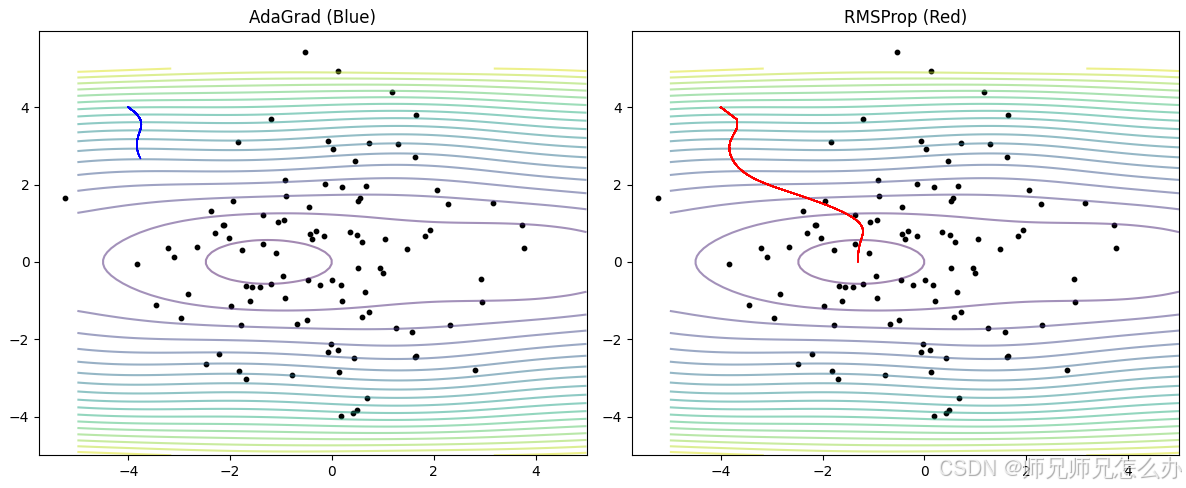
以下是使用python编写的两个算法的动画对比图，可以观察到RMSProp算法相比AdaGrad算法会快速往原点滑动，然后在原点附近来回滑动，通过修改超参可以调整算法的步幅以及方向，建议各位自行尝试：

代码源码如下：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation# 生成样本数据
np.random.seed(42)
sample_data = np.random.randn(100, 2) * 2# 定义测试函数
def loss_func(x, y):return 0.1 * x ** 2 + 2 * y ** 2 + np.sin(x) * np.cos(y)# 优化器实现
class AdaGrad:def __init__(self, params, lr=0.1):self.params = params.copy()self.lr = lrself.cache = {k: 0 for k in params.keys()}self.history = {k: [v] for k, v in params.items()}def step(self, grads):for key in self.params:self.cache[key] += grads[key] ** 2self.params[key] -= self.lr * grads[key] / (np.sqrt(self.cache[key]) + 1e-8)self.history[key].append(self.params[key])class RMSProp:def __init__(self, params, lr=0.1, gamma=0.9):self.params = params.copy()self.lr = lrself.gamma = gammaself.cache = {k: 0 for k in params.keys()}self.history = {k: [v] for k, v in params.items()}def step(self, grads):for key in self.params:self.cache[key] = self.gamma * self.cache[key] + (1 - self.gamma) * grads[key] ** 2self.params[key] -= self.lr * grads[key] / (np.sqrt(self.cache[key]) + 1e-8)self.history[key].append(self.params[key])# 初始化优化器
initial_params = {'x': -4, 'y': 4}
adagrad = AdaGrad(initial_params.copy())
rmsprop = RMSProp(initial_params.copy())# 创建可视化
fig = plt.figure(figsize=(12, 5))
ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)# 绘制样本数据
ax1.scatter(sample_data[:, 0], sample_data[:, 1], c='black', s=10)
ax2.scatter(sample_data[:, 0], sample_data[:, 1], c='black', s=10)# 绘制等高线
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = loss_func(X, Y)
ax1.contour(X, Y, Z, levels=20, alpha=0.5)
ax2.contour(X, Y, Z, levels=20, alpha=0.5)# 动画更新函数
def update(frame):# 计算梯度x_adagrad, y_adagrad = adagrad.params['x'], adagrad.params['y']grads = {'x': 0.2 * x_adagrad + np.cos(x_adagrad) * np.cos(y_adagrad),'y': 4 * y_adagrad - np.sin(x_adagrad) * np.sin(y_adagrad)}adagrad.step(grads)x_rmsprop, y_rmsprop = rmsprop.params['x'], rmsprop.params['y']grads = {'x': 0.2 * x_rmsprop + np.cos(x_rmsprop) * np.cos(y_rmsprop),'y': 4 * y_rmsprop - np.sin(x_rmsprop) * np.sin(y_rmsprop)}rmsprop.step(grads)# 更新轨迹ax1.plot(adagrad.history['x'], adagrad.history['y'], 'b-', lw=1)ax2.plot(rmsprop.history['x'], rmsprop.history['y'], 'r-', lw=1)return ax1, ax2# 运行动画
ani = FuncAnimation(fig, update, frames=100, interval=200)
ax1.set_title('AdaGrad (Blue)')
ax2.set_title('RMSProp (Red)')
plt.tight_layout()
plt.show()