简介

线段树是一种应用极其广泛，使用范围较广并且非常知名的树形数据结构，主要用于进行区间操作，如区间修改，区间查询等。这种数据结构唯一的不足就是巨大的代码量，因此处理一些较简单的问题时建议用树状数组。

原理

其实线段树的原理是比较简单的。我们平常见到的树都是没有特殊含义的，而线段树的每个点都表示一个区间。详细来讲，线段树其实是一颗二叉树，我们会把一个数组转换成一颗这样的树并进行多种操作。这是一颗线段树的大致样子。

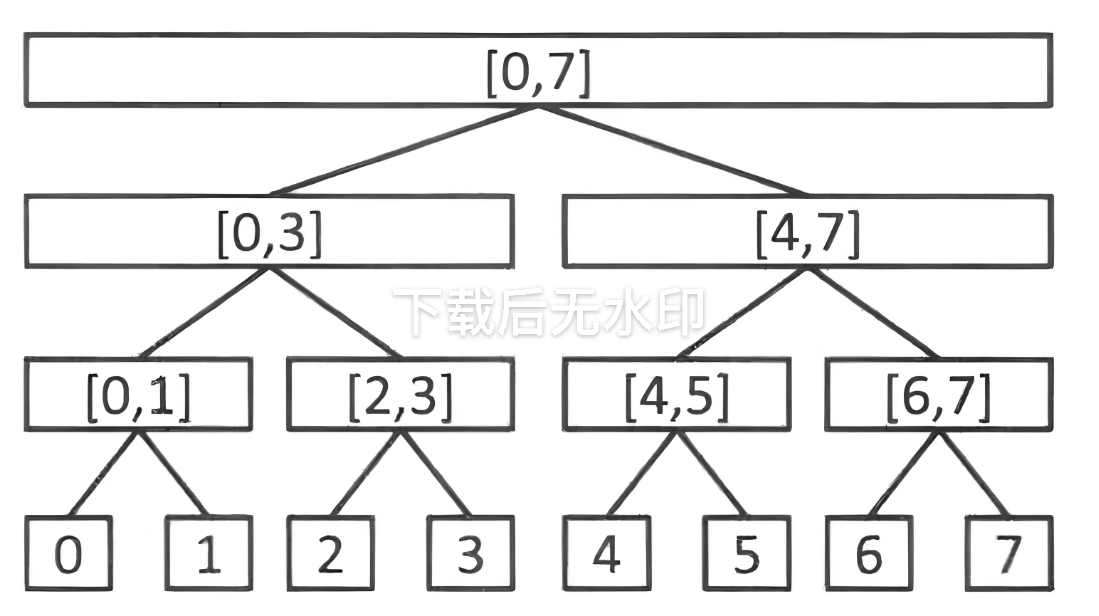
可以看见，父节点表示的区间是两个子节点表示的区间拼出来的。但是如果不知道父节点或子节点是谁这颗树维护不了，我们因此可以定义一个结点u，并设它的左儿子为u*2,右儿子为u*2+1。这样子就不可能存在重复结点的情况。当然这样会消耗大量空间，因此要用到优化，我们待会儿讲。

可以看出来如果想表示区间中的一段只需把这些分散的区间组合起来。那我们应该怎么组合？我们假设查询的区间为[l,r],如果我们检测到一个区间被完全包含我们就返回它的值。否则，我们取该区间的中间，把这个区间割开。如果检测到查询区间有一部分在左边的区间，我们去查左边。查右边同理。这样，我们可以以logn的复杂度把序列多余的部分一点一点消掉，直到无法查询为止。

举个例子，我们现在要在上图中查询[1,3]的值。首先我们从结点1开始，这里没有完全包含，我们把结点1的区间从中间切开，变为[0,3]和[4,7],可以看出[4,7]与查询区间完全不包含，我们转而搜索[0,3]。

因为[0,3]依旧不是完全包含，我们将它切开，这是[2,3]被确定为完全包含，我们记录[2,3]的值，发现[0,1]里只有1包含，我们把它提出来，这样我们就把[1,3]拆成了1和[2,3]。

这时我们就完成了区间查询，但我们可能还需要进行区间修改。怎么做呢？我们只需让每个结点多维护一个懒标记。这个东西非常重要，因为如果每次我们都要把所有修改区间的子区间修改一遍复杂度不如直接修改。我们发现我们如果已经像之前把修改区间拆开，它们下面的结点目前没有必要改，我们完全可以等搜到子节点以后再改。这样修改也变成了logn的。

具体怎么操作？我们假设进行加操作，每次我们把修改的区间的懒标记加上修改值，等到有需要访问子节点的操作时，我们把子节点的和加上其区间长度乘懒标记的值，并把懒标记加给左右儿子，最后把自己的懒标记清空就可以了。

实现

建树

struct tree{int l,r,sum,lazy;
}t[4*N];
void build(int u, int l, int r){t[u].l=l,t[u].r=r;if(l==r){t[u].sum=a[l];return;}int mid=(l+r)>>1;build(u*2,l,mid), build(u*2+1,mid+1,r);t[u].sum=t[u*2].sum+t[u*2+1].sum;
}

这里的u就是每个树上结点的编号，l和r表示这个结点表示的区间。当l=r说明这个结点表示一个元素，直接赋值即可。在搜索完子节点我们更新父节点的和。

懒标记下传

void pushdown(int u){if(t[u].lazy){t[u*2].sum+=t[u].lazy*(t[u*2].r-t[u*2].l+1);t[u*2+1].sum+=t[u].lazy*(t[u*2+1].r-t[u*2+1].l+1);t[u*2].lazy+=t[u].lazy, t[u*2+1].lazy+=t[u].lazy;t[u].lazy=0;		}
}

这里的lazy就是懒标记，这里我们把父节点的懒标记加给两个子节点，同时维护原来就该加的值。

区间修改

void update(int u, int l, int r, int c){if(t[u].l>=l&&t[u].r<=r){t[u].sum+=c*(t[u].r-t[u].l+1);t[u].lazy+=c;return;}pushdown(u);int mid=(t[u].l+t[u].r)>>1;if(mid>=l) update(u*2,l,r,c);if(r>mid) update(u*2+1,l,r,c);t[u].sum=t[u*2].sum+t[u*2+1].sum;
}

这里的l,r,c都是区间加的参数，不会变，真正表示结点信息的是u。我们看上面的判断表示如果这个结点表示的区间被完全包含我们就给它带上懒标记，维护区间和。如果不完全包含我们就需要下传懒标记让每次查询时获得的都是正确的值。这里我们去中间值将区间拆开。r需要大于mid是因为第二个区间的左端点是mid+1,我们需要判断一下，这里写r>=mid+1也是可以的。

区间查询

int find(int u, int l, int r){if(t[u].l>=l&&t[u].r<=r) return t[u].sum;pushdown(u);int ans=0, mid=(t[u].l+t[u].r)>>1;if(mid>=l) ans+=find(u*2,l,r);if(r>mid) ans+=find(u*2+1,l,r);return ans;
}

这里的l，r同样是查询区间的左右端点，不会改变。可以看到我们每次查询儿子前都要下传懒标记，这样儿子的值才是对的。我们只需维护一个计数器一层一层把答案传上来即可。

优化

假设一个序列特别长，有一千万个元素。这个时候开4倍空间会爆炸。这时我们就要用到动态开点。我们怎么做？之前定义了u的左儿子是u*2,右儿子是u*2+1,但这样可能浪费大量空间。我们因此取消这个定义，维护一个计数器，表示目前有多少点。我们存两个变量表示一个结点的儿子，每次添加时我们让这个变量变成计数器，然后计数器++。

这样我们可以节省大量空间，但代码也极度复杂，这里就不放了。推荐一下OIwiki的模版。

例题及完整代码

区间加区间查模版

代码：

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
int n,m,a[N],op,x,y,k;
struct tree{int l,r,sum,lazy;
}t[4*N];
void build(int u, int l, int r){t[u].l=l,t[u].r=r;if(l==r){t[u].sum=a[l];return;}int mid=(l+r)>>1;build(u*2,l,mid), build(u*2+1,mid+1,r);t[u].sum=t[u*2].sum+t[u*2+1].sum;
}
void pushdown(int u){if(t[u].lazy){t[u*2].sum+=t[u].lazy*(t[u*2].r-t[u*2].l+1);t[u*2+1].sum+=t[u].lazy*(t[u*2+1].r-t[u*2+1].l+1);t[u*2].lazy+=t[u].lazy, t[u*2+1].lazy+=t[u].lazy;t[u].lazy=0;		}
}
void update(int u, int l, int r, int c){if(t[u].l>=l&&t[u].r<=r){t[u].sum+=c*(t[u].r-t[u].l+1);t[u].lazy+=c;return;}pushdown(u);int mid=(t[u].l+t[u].r)>>1;if(mid>=l) update(u*2,l,r,c);if(r>mid) update(u*2+1,l,r,c);t[u].sum=t[u*2].sum+t[u*2+1].sum;
}
int find(int u, int l, int r){if(t[u].l>=l&&t[u].r<=r) return t[u].sum;pushdown(u);int ans=0, mid=(t[u].l+t[u].r)>>1;if(mid>=l) ans+=find(u*2,l,r);if(r>mid) ans+=find(u*2+1,l,r);return ans;
}
signed main(){cin>>n>>m;for(int i=1;i<=n;i++) cin>>a[i];build(1,1,n);while(m--){cin>>op;if(op==1){cin>>x>>y>>k;update(1,x,y,k);}else{cin>>x>>y;cout<<find(1,x,y)<<endl;}}return 0;
}

线段树进阶题目

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
int n,q,mod,a[N],op,x,y,k;
struct tree{int l,r,sum,mul,add;
}t[4*N];
void build(int u, int l, int r){t[u].l=l,t[u].r=r,t[u].mul=1;if(l==r){t[u].sum=a[l]%mod;return;}int mid=(l+r)>>1;build(u*2,l,mid);build(u*2+1,mid+1,r);t[u].sum=t[u*2].sum+t[u*2+1].sum;t[u].sum%=mod;
}
void pushd(int u){if(t[u].mul!=1||t[u].add){int L=u*2,R=u*2+1;t[L].sum=(1ll*t[L].sum*t[u].mul+t[u].add*(t[L].r-t[L].l+1))%mod;t[R].sum=(1ll*t[R].sum*t[u].mul+t[u].add*(t[R].r-t[R].l+1))%mod;t[L].mul=(1ll*t[L].mul*t[u].mul)%mod;t[R].mul=(1ll*t[R].mul*t[u].mul)%mod;t[L].add=(1ll*t[L].add*t[u].mul+t[u].add)%mod;t[R].add=(1ll*t[R].add*t[u].mul+t[u].add)%mod;t[u].mul=1,t[u].add=0;}
}
void update1(int u, int l, int r, int k){if(t[u].l>=l&&t[u].r<=r){t[u].sum=(1ll*t[u].sum*k)%mod;t[u].mul=(1ll*t[u].mul*k)%mod;t[u].add=(1ll*t[u].add*k)%mod;return;}pushd(u);int mid=(t[u].l+t[u].r)>>1;if(l<=mid) update1(u*2,l,r,k);if(r>mid) update1(u*2+1,l,r,k);t[u].sum=(t[u*2].sum+t[u*2+1].sum)%mod;
}
void update2(int u, int l, int r, int k){if(t[u].l>=l&&t[u].r<=r){t[u].sum=(t[u].sum+1ll*k*(t[u].r-t[u].l+1))%mod;t[u].add=(t[u].add+k)%mod;return;}pushd(u);int mid=(t[u].l+t[u].r)>>1;if(l<=mid) update2(u*2,l,r,k);if(r>mid) update2(u*2+1,l,r,k);t[u].sum=(t[u*2].sum+t[u*2+1].sum)%mod;
}
int find(int u, int l, int r){if(t[u].l>=l&&t[u].r<=r) return t[u].sum;pushd(u);int mid=(t[u].l+t[u].r)>>1,ans=0;if(l<=mid) ans+=find(u*2,l,r);if(r>mid) ans+=find(u*2+1,l,r);return ans;
}
signed main(){cin>>n>>q>>mod;for(int i=1;i<=n;i++) cin>>a[i];build(1,1,n);while(q--){cin>>op;if(op==1){cin>>x>>y>>k;update1(1,x,y,k);}else if(op==2){cin>>x>>y>>k;update2(1,x,y,k);}else{cin>>x>>y;cout<<find(1,x,y)%mod<<endl;}}return 0;
}

这里再给大家推荐几个题单。

适合入门的题单

适合进阶的题单