一、核心思想：一个形象的比喻

二、核心思想的具体拆解

步骤一：构建FP-tree（频繁模式树）

步骤二：从FP-tree中挖掘频繁项集

为什么这很高效？

三、总结

核心思想与优势

适用场景与缺点

四、例题

给定数据

第一步：第一次扫描数据库，找出频繁1项集及其支持度

第二步：第二次扫描数据库，构建FP-tree

第三步：挖掘FP-tree，寻找频繁项集

1. 以后缀 A 开始挖掘

步骤 1: 寻找条件模式基 (Conditional Pattern Base)

步骤 2: 构建条件FP-tree (Conditional FP-tree) for A

步骤 3: 挖掘条件FP-tree并生成频繁项集

2. 以后缀 E 开始挖掘

步骤 1: 寻找条件模式基 for E

步骤 2: 构建条件FP-tree for E

步骤 3: 挖掘条件FP-tree for E

3. 以后缀 C 开始挖掘

步骤 1: 寻找条件模式基 for C

步骤 2: 构建条件FP-tree for C

步骤 3: 挖掘条件FP-tree for C

4. 以后缀 B 开始挖掘

步骤 1: 寻找条件模式基 for B

步骤 2: 构建条件FP-tree for B

步骤 3: 挖掘条件FP-tree for B

第四步：汇总所有频繁项集

最终答案

参考：

Python数据挖掘实战：微课版 - 9.3 FP-growth算法 - 王磊邱江涛 - 微信读书

19.FpGrowth算法介绍_哔哩哔哩_bilibili
9.2 利用FP-tree挖掘频繁项集的过程

FP-growth（Frequent Pattern Growth，频繁模式增长）算法是用于高效挖掘数据集中频繁项集的一种方法。它极大地改进了传统的Apriori算法，核心目标仍然是找出所有满足最小支持度阈值的项集。

其核心思想可以概括为：“分而治之” 和 “用空间换时间”。

一、核心思想：一个形象的比喻

想象一下，你要统计一图书馆里所有书籍的组合借阅情况（比如，同时被借阅的书籍组合）。

Apriori算法（传统方法）：像一个笨拙的图书管理员。他需要反复穿梭于各个书架之间，每次只关心“2本书的组合”，统计完后再找“3本书的组合”，如此反复。这个过程会产生大量的“候选组合”，并且需要反复扫描整个借阅记录（数据库），非常耗时。
FP-growth算法（新方法）：像一个聪明的图书管理员。他首先花一点时间，为整个图书馆建立了一个非常精巧的索引目录（FP-tree）。这个目录不仅记录了每本书被借阅的次数，还清晰地记录了哪些书经常被一起借阅。当你想查询任何书籍组合时，他无需再跑回书架，只需在这个浓缩的目录里进行查找和拼接，就能快速得到结果。

这个“精巧的目录”就是FP-growth算法的精髓。

二、核心思想的具体拆解

FP-growth算法主要分为两个核心步骤，完美体现了其思想：

步骤一：构建FP-tree（频繁模式树）

这是“用空间换时间”和“数据压缩”的体现。

第一次扫描数据库：统计所有单项（1项集）的支持度，并丢弃那些不频繁的项（低于最小支持度）。
排序：将剩余的频繁项按照支持度从高到低排序。这样做的好处是，出现频率高的项更靠近树的根部，使得树的深度尽可能小，更加紧凑。
第二次扫描数据库：开始构建FP-tree。
- 将每条事务（例如一次购物篮记录 {牛奶，面包，啤酒}）中的项按第二步的顺序排序和过滤（例如排序后为 {啤酒，面包，牛奶}）。
- 从树的根节点开始，为这条事务创建一条分支。如果分支的前缀与已有路径共享，则共享节点的计数加1；如果不共享，则创建新的节点。
- 同时，为了快速访问树中的节点，还维护了一个头指针表，它链接了所有相同名称的节点。

为什么这很巧妙？

压缩数据库：原始的数据库被压缩成了一棵FP-tree。事务数据中共享的频繁项被合并到了同一条路径上，大大减少了存储空间。
信息完整：这棵树完整地保留了项集之间的关联和频率信息。

步骤二：从FP-tree中挖掘频繁项集

这是“分而治之”思想的体现。

挖掘过程是递归的。我们不是从整个大树开始挖，而是从小树枝开始。

从后缀开始：从头指针表中支持度最低的项（即树的枝叶末梢）开始，作为当前的后缀模式（例如 {牛奶}）。
寻找条件模式基：沿着头指针表，找到FP-tree中所有包含此后缀的路径。这些路径去掉后缀后剩下的前缀部分，以及路径上的计数，就构成了条件模式基。这相当于为“牛奶”这个项创建了一个子数据库。
构建条件FP-tree：以这个条件模式基作为新的“数据库”，重复步骤一的过程，构建一个只与“牛奶”相关的条件FP-tree。
递归挖掘：如果条件FP-tree不是空的（例如一条单路径），则递归地挖掘这棵小树。如果它是一条单路径，则直接生成该路径上所有节点的组合，并与后缀模式合并，即可得到所有频繁项集（例如，从路径 啤酒：3，面包：3 可以得到 {啤酒，面包，牛奶}，{啤酒，牛奶}，{面包，牛奶}）。
移动指针：处理完一个后缀后，就回头指针表中移动到下一个支持度稍高的项（例如 {面包}），重复步骤2-4，直到处理完所有项。

为什么这很高效？

分治：将挖掘整个大数据集的任务，分解为挖掘多个更小的条件数据库的任务，问题规模指数级减小。
避免候选集生成：它不需要产生大量的候选集（这是Apriori的主要瓶颈），而是通过递归和直接拼接来生成频繁项集。
无重复扫描数据库：整个过程中，原始数据库只被扫描了两次（构建FP-tree时）。之后的所有操作都是在内存中对这棵压缩树进行操作，速度极快。

三、总结

核心思想与优势

方面	核心思想阐述	带来的优势
数据表示	用空间换时间：花费内存构建一个高度压缩、信息完整的数据结构（FP-tree）。	大幅减少I/O开销：仅需扫描数据库两次，后续操作均在内存中进行。
挖掘策略	分而治之：通过递归地构建条件模式基和条件FP-tree，将大问题分解为多个小问题。	效率极高：避免了产生海量候选集，算法复杂度通常远低于Apriori。
搜索方法	模式增长：从后缀模式出发，通过拼接前缀路径来直接生成频繁模式，而非通过候选和测试。	精准高效：没有无效的候选集生成和测试过程。

适用场景与缺点

适用场景：非常适合挖掘稠密数据集（即事务中项之间相关性较强，共享前缀多），能获得很好的压缩效果和性能提升。
缺点：
- 空间消耗：FP-tree及其递归过程中构建的条件FP-tree可能会消耗大量内存，尤其是在处理稀疏数据集或支持度阈值很低时。
- 实现复杂度：相对于Apriori，其实现更为复杂。

FP-growth算法的核心在于创新地使用树结构来压缩存储数据，并基于此结构采用分而治之的策略进行高效挖掘，从而解决了Apriori算法多次扫描数据库和产生大量候选集的两个主要性能瓶颈。

四、例题

给定数据

TID	Items
10	A, C, D
20	B, C, E
30	A, B, C, E
40	B, E

设定最小支持度 (min_sup)： 为了演示方便，我们设定最小支持度为 2 (即出现次数 >= 2)。

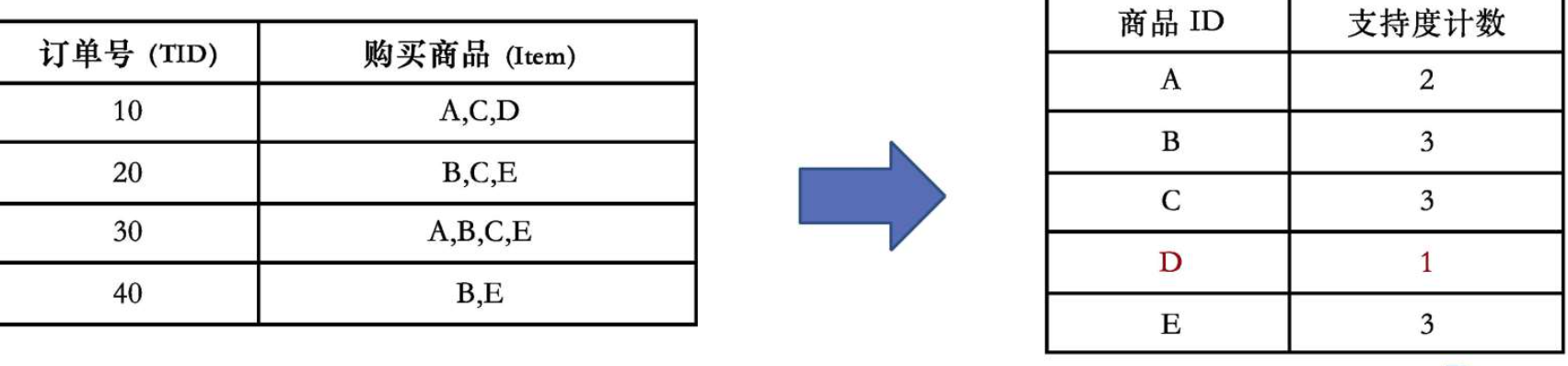
第一步：第一次扫描数据库，找出频繁1项集及其支持度

我们统计每个商品在所有订单中出现的总次数。

A: 出现在T10, T30 → 计数 = 2
B: 出现在T20, T30, T40 → 计数 = 3
C: 出现在T10, T20, T30 → 计数 = 3
D: 出现在T10 → 计数 = 1 (小于min_sup=2，丢弃)
E: 出现在T20, T30, T40 → 计数 = 3

筛选并排序后的频繁1项集（按支持度降序排列）：

商品	支持度
B	3
C	3
E	3
A	2

顺序为: B, C, E, A (支持度相同时，顺序可任意，但必须固定)

第二步：第二次扫描数据库，构建FP-tree

我们为每条事务（订单）中的商品按照上一步确定的顺序（B, C, E, A）进行排序，并过滤掉非频繁项（此例中为D）。

T10: A, C, D → 过滤D → A, C → 按顺序排序 → C, A (因为C的支持度3 > A的支持度2)
T20: B, C, E → 按顺序排序 → B, C, E
T30: A, B, C, E → 按顺序排序 → B, C, E, A
T40: B, E → 按顺序排序 → B, E

现在，我们开始构建FP-tree。Root是根节点，为空。

插入 T10: C, A

从Root开始，创建子节点 C:1。
从 C:1 开始，创建子节点 A:1。

插入 T20: B, C, E

从Root开始，没有 B 子节点，创建 B:1。
从 B:1 开始，创建子节点 C:1。
从 C:1 开始，创建子节点 E:1。

插入 T30: B, C, E, A

从Root开始，已有 B 子节点，将其计数加1 → B:2。
从 B:2 开始，已有 C 子节点，将其计数加1 → C:2。
从 C:2 开始，已有 E 子节点，将其计数加1 → E:2。
从 E:2 开始，没有 A 子节点，创建新的子节点 A:1。

插入 T40: B, E

从Root开始，已有 B 子节点，将其计数加1 → B:3。
从 B:3 开始，没有 E 子节点（B的子节点目前是 C:2，不是 E），因此创建一个新的子节点 E:1。

最终构建的FP-tree如下图所示：
(为了清晰，我们同时维护一个头指针表，将相同名称的节点链接起来)

        Root/    \B:3    C:1/   \      \E:1   C:2    A:1\E:2\A:1

头指针表 (Header Table):

B → 链接到 (B:3)
C → 链接到 (C:1) -> (C:2)
E → 链接到 (E:1) -> (E:2)
A → 链接到 (A:1) -> (A:1)

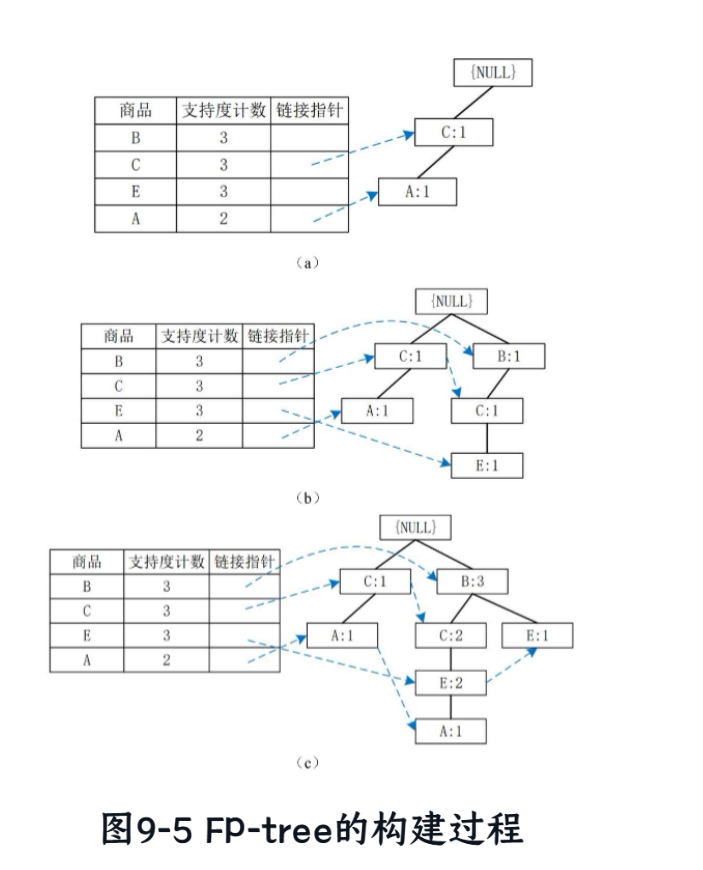
第三步：挖掘FP-tree，寻找频繁项集

我们从头指针表底部的支持度最低的项开始（即A），然后向上是E，C，最后是B。

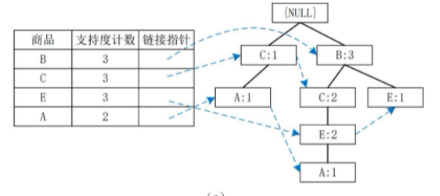
1. 以后缀 `A` 开始挖掘

步骤 1: 寻找条件模式基 (Conditional Pattern Base)
- 在FP-tree中，找到所有以 A 结尾的路径。
- 路径1: C:1 -> A:1 (来自T10 C, A)
  - 前缀路径: C:1
- 路径2: B:3 -> C:2 -> E:2 -> A:1 (来自T30 B, C, E, A)
  - 前缀路径: B:3, C:2, E:2
- A 的条件模式基是 {C:1} 和 {B:3, C:2, E:2}。
步骤 2: 构建条件FP-tree (Conditional FP-tree) for A
- 以条件模式基作为新的事务数据库。
- 事务1: C (计数为1)
- 事务2: B, C, E (计数为路径上的最小值，即 A 的计数1？这里需要修正：计数应取路径末尾目标节点A的计数，即每条前缀路径的计数应等于该路径上A节点的计数)
  - 修正：路径 C:1 -> A:1，A的计数是1，所以前缀路径 C 的计数是1。
  - 路径 B:3, C:2, E:2 -> A:1，A的计数是1，所以前缀路径 B, C, E 的计数是1。
- 现在统计这个新“数据库”中项的支持度：
  - C: 1 (来自事务1) + 1 (来自事务2) = 2
  - B: 1 (来自事务2) = 1 (< min_sup=2，丢弃)
  - E: 1 (来自事务2) = 1 (< min_sup=2，丢弃)
- 频繁项只有 C:2。
- 条件FP-tree for A 是一条单路径 C:2。
步骤 3: 挖掘条件FP-tree并生成频繁项集
- 条件FP-tree是单路径 C:2。
- 该路径上所有项的非空组合与后缀 A 合并，即可得到频繁项集：
  - {C} + {A} = {C, A} (支持度 = min(2, ...) ，通常取条件模式基中计数的汇总，这里 {C,A} 的支持度是 C:1路径的1 + B,C,E:1路径的1？ 更准确的做法：项集的支持度是其条件FP-tree根节点的计数？这里我们最终看原始计数)
  - 从原始数据看，{C, A} 出现在T10和T30，支持度确实是2。
- 所以，以后缀 A 挖掘出的频繁项集是: {C, A} (支持度2)。

结论：包含A的频繁项集为 {A} (2), {C,A} (2)。 ({A} 本身是频繁1项集)

（应该是：由于项目{B},{E}不满足最小支持度计数阈值，所以被删除。）

2. 以后缀 `E` 开始挖掘

步骤 1: 寻找条件模式基 for E
- 在FP-tree中，找到所有以 E 结尾的路径。
- 路径1: B:3 -> C:2 -> E:2 (来自T20和T30 B,C,E)
  - 前缀路径: B:3, C:2 (计数为 E 的计数2)
- 路径2: B:3 -> E:1 (来自T40 B,E)
  - 前缀路径: B:3 (计数为 E 的计数1)
- E 的条件模式基是 {B:3, C:2} (计数2) 和 {B:3} (计数1)。
步骤 2: 构建条件FP-tree for E
- 事务1: B, C (计数2)
- 事务2: B (计数1)
- 统计新数据库支持度：
  - B: 2 + 1 = 3 (>=2，保留)
  - C: 2 (>=2，保留)
- 按支持度降序排序：B, C。
- 构建条件FP-tree：
  - 插入 B, C (计数2): Root -> B:2 -> C:2
  - 插入 B (计数1): Root -> B:2 (计数+1=3)
- 最终的条件FP-tree for E:
```
Root|B:3|C:2
```
步骤 3: 挖掘条件FP-tree for E————（看不懂？）末尾有解释
- 条件FP-tree不是空树也不是单路径，需要递归挖掘。
- 首先，以后缀 {C, E} 开始挖掘 (从条件FP-tree的底部项C开始)
  - 寻找 {C, E} 的条件模式基: 在 E 的条件FP-tree中，找到所有以 C 结尾的路径。路径：B:3 -> C:2。
    - 前缀路径: B:3 (计数为 C 的计数2)
  - 构建 {C, E} 的条件FP-tree:
    - 事务: B (计数2)
    - 统计支持度：B:2 (>=2，保留)
    - 条件FP-tree for {C,E} 是单路径 B:2。
  - 挖掘 {C,E} 的条件FP-tree:
    - 生成组合: {B} + {C,E} = {B, C, E} (支持度2？原始数据中出现在T20和T30，支持度2)
  - 所以，包含 {C,E} 的频繁项集: {C,E}, {B,C,E}。
    - {C,E} 的支持度：从其条件模式基 B:3(计数2) 可以看出计数为2。原始数据中出现在T20和T30，支持度2。
- 然后，处理后缀 {E} 本身：条件FP-tree中有 B:3，所以 {B, E} 是频繁的。
- 最终，包含 E 的频繁项集:
  - {E} (3)
  - {B, E} (3) (来自条件FP-tree中的 B:3)
  - {C, E} (2) (来自上面的挖掘)
  - {B, C, E} (2) (来自上面的挖掘)

3. 以后缀 `C` 开始挖掘

步骤 1: 寻找条件模式基 for C
- 在FP-tree中，找到所有以 C 结尾的路径。
- 路径1: B:3 -> C:2 (来自T20和T30 B,C,...)
  - 前缀路径: B:3 (计数为 C 的计数2)
- 路径2: Root -> C:1 (来自T10 C,...)
  - 前缀路径: {} (空，计数为 C 的计数1)
- C 的条件模式基是 {B:3} (计数2) 和 {} (计数1)。
步骤 2: 构建条件FP-tree for C
- 事务1: B (计数2)
- 事务2: {} (空集，计数1) //空集无法形成项集，忽略
- 统计支持度：B:2 (>=2，保留)
- 条件FP-tree for C 是单路径 B:2。
步骤 3: 挖掘条件FP-tree for C
- 条件FP-tree是单路径 B:2。
- 生成组合: {B} + {C} = {B, C} (支持度2)
- 所以，包含 C 的频繁项集:
  - {C} (3)
  - {B, C} (2)

4. 以后缀 `B` 开始挖掘

步骤 1: 寻找条件模式基 for B
- 在FP-tree中，找到所有以 B 结尾的路径。B 是直接挂在Root下的。
- 路径: Root -> B:3
  - 前缀路径: {} (空，计数为 B 的计数3)
- B 的条件模式基是空。
步骤 2: 构建条件FP-tree for B
- 条件模式基是空，因此条件FP-tree为空。
步骤 3: 挖掘条件FP-tree for B
- 无法生成新的频繁项集。
- 包含 B 的频繁项集只有它自己: {B} (3)。

第四步：汇总所有频繁项集

将所有步骤中找到的频繁项集汇总，并去重（{A}, {B}, {C}, {E} 在第一步已得到）。

频繁1项集 (Frequent 1-itemsets):

{A}: 2
{B}: 3
{C}: 3
{E}: 3

频繁2项集 (Frequent 2-itemsets):

{C, A}: 2
{B, E}: 3
{C, E}: 2
{B, C}: 2

频繁3项集 (Frequent 3-itemsets):

{B, C, E}: 2

频繁4项集 (Frequent 4-itemsets):

至此，我们使用FP-growth算法完整地找出了给定数据集中的所有频繁项集。整个过程的核心在于构建FP-tree并通过递归挖掘条件模式基来避免生成大量的候选集。

最终答案

Python数据挖掘实战：微课版 - 9.3 FP-growth算法 - 王磊邱江涛 - 微信读书

细节补充

我们现在的任务是从 E的条件FP-tree 里挖宝贝。这棵树长这样：

(Root)|
(B:3)|
(C:2)

目标：找到所有带 E 的宝贝组合（比如 {B,E}, {C,E}, {B,C,E}）。

第一步：看树，直接拿到第一个宝贝

树上写着 B:3。
意思是：B 和 E 一起出现了 3 次。
✅ 所以，我们找到了第一个宝贝：{B, E}

第二步：处理树上的下一个点 `C`

树上还有一个 C:2，挂在 B 下面。我们不能直接用它，需要“放大镜”看仔细。

为什么要为 {C,E} 再建一棵树？
答：为了搞清楚 C 是和谁一起出现的，这样才能拼出更大的宝贝。

怎么做？3个小步：

找 C 的路径：在 E 的树里，找到通到 C 的路。只有一条：B -> C。
看这条路的意思：这条路 B -> C 计数是2。
- 翻译：B、C、E 这三个家伙一起出现了 2 次。
建新树：我们就为 C 和 E 这个组合，建一棵超小的新树，只记录和它俩一起玩的人。
- 这棵新树只有：(B:2)
- 意思：和 C、E 一起玩的，只有 B，而且玩了2次。

第三步：挖这棵超小的新树

新树 (B:2) 非常简单，一眼就能看穿。

它告诉我们两件事：
1. ✅ {C, E} 这个组合自己出现了 2 次。（因为 B 出现2次的前提是 C 和 E 肯定也在）
2. ✅ {B, C, E} 这个更大的组合出现了 2 次。（就是 B 自己加上 C 和 E）

最终我们找到了所有带 `E` 的宝贝：

从 E 的树本身：{B, E} (3次)

从为 {C,E} 建的小树里：{C, E} (2次)，{B, C, E} (2次)

(再加上最开始就知道的 {E} 自己)

FP-growth算法经典面试题

1. 请简要说明FP-growth算法的核心思想是什么？

高分回答：
“FP-growth算法的核心思想是‘分而治之’和‘用空间换时间’。它通过两次扫描数据库，构建一个高度压缩的数据结构——FP树(Frequent Pattern Tree)，将原始数据完整的频次信息压缩存储在其中。后续的挖掘过程不再需要反复访问原始数据库，而是通过递归地在FP树上构建条件模式基和条件FP树来挖掘全部的频繁项集。这种方法完美避免了Apriori算法中耗时的候选集生成与测试过程。”

关键词： 分而治之、空间换时间、FP树、两次扫描、条件模式基、递归挖掘、避免候选集生成。

2. 和Apriori算法相比，FP-growth有什么优缺点？

高分回答：
“优点是效率非常高。主要体现在两方面：第一，它通常只需要扫描两次数据库，而Apriori需要扫描K+1次（K为最长频繁项集长度），I/O开销大大减少。第二，它不产生候选集，彻底避免了Apriori中候选集数量爆炸的问题。

缺点主要是空间消耗可能较大。FP-tree及其递归构建的条件FP-tree需要存储在内存中，当数据集非常稀疏或最小支持度设置得很低时，树的规模可能会很大，对内存是一个考验。”

背诵模板：

优点：快。 扫描次数少（2次 vs. K+1次），无候选集。
缺点：可能占内存。 树结构在密集数据下压缩性好，但稀疏数据下可能内存消耗大。

3. 解释一下什么是“条件模式基”(Conditional Pattern Base)？

高分回答：
“条件模式基是FP-growth算法递归挖掘过程中的一个核心概念。当我们要挖掘以某个项（比如项X）为后缀的所有频繁项集时，我们需要在FP树中找到所有包含X的路径。这些路径中，去掉后缀项X之后的前缀部分，以及路径的计数信息，就共同构成了项X的条件模式基。它本质上是一个子数据库，记录了所有与X频繁共现的项及其频次，是构建更小子树（条件FP-tree）的基础。”

关键词： 包含X的路径、去掉X后的前缀、子数据库、构建条件FP-tree的基础。

4. FP-growth算法在什么情况下效率会下降？

高分回答：
“主要在两种情况下效率会相对下降：

数据集非常稀疏时：这意味着事务中物品的共同前缀很少，导致构建出的FP-tree分支很多，压缩效果不佳，树会变得又宽又浅，占用大量内存，递归挖掘的效率也会降低。
最小支持度阈值设置得非常低时：这会导致大量非频繁的项变成频繁项，使得FP-tree的规模变得非常大，同样会消耗大量内存和计算资源。”

关键词： 数据稀疏、支持度阈值低、树结构庞大、内存消耗大。

5. (可选) 能画一下FP-tree的基本结构吗？

如果问到，你可以画一个简单的示意图并解释：

        Root/  \B:3   C:1/   \     \C:2   E:1    A:1\E:2\A:1

解释： “从上到下表示项的先后顺序，节点上的数字是计数。从根节点到任意一个节点就形成一条路径，代表一个项集的出现模式。比如 B:3 -> C:2 -> E:2 这条路径，表示项集 {B, C, E} 出现了2次。”

面试实战技巧

先总后分：先一句话总结核心思想，再应要求展开细节。
对比突出：谈到FP-growth，必提Apriori，用对比凸显你的理解深度。
扬长避短：问优缺点时，先说优点，再“诚实”地提到缺点，并说明在什么情况下缺点会成为问题。
自信背诵：把这些答案背熟，面试时就能脱口而出，显得非常熟练。

一、核心思想：一个形象的比喻

二、核心思想的具体拆解

步骤一：构建FP-tree（频繁模式树）

步骤二：从FP-tree中挖掘频繁项集

为什么这很高效？

三、总结

核心思想与优势

适用场景与缺点

四、例题

给定数据

第一步：第一次扫描数据库，找出频繁1项集及其支持度

第二步：第二次扫描数据库，构建FP-tree

第三步：挖掘FP-tree，寻找频繁项集

1. 以后缀 A 开始挖掘

步骤 1: 寻找条件模式基 (Conditional Pattern Base)

步骤 2: 构建条件FP-tree (Conditional FP-tree) for A

步骤 3: 挖掘条件FP-tree并生成频繁项集

2. 以后缀 E 开始挖掘

步骤 1: 寻找条件模式基 for E

步骤 2: 构建条件FP-tree for E

步骤 3: 挖掘条件FP-tree for E————（看不懂？）末尾有解释

3. 以后缀 C 开始挖掘

步骤 1: 寻找条件模式基 for C

步骤 2: 构建条件FP-tree for C

步骤 3: 挖掘条件FP-tree for C

4. 以后缀 B 开始挖掘

步骤 1: 寻找条件模式基 for B

步骤 2: 构建条件FP-tree for B

步骤 3: 挖掘条件FP-tree for B

第四步：汇总所有频繁项集

最终答案

细节补充

第一步：看树，直接拿到第一个宝贝

第二步：处理树上的下一个点 C

第三步：挖这棵超小的新树

最终我们找到了所有带 E 的宝贝：

FP-growth算法经典面试题

1. 请简要说明FP-growth算法的核心思想是什么？

2. 和Apriori算法相比，FP-growth有什么优缺点？

3. 解释一下什么是“条件模式基”(Conditional Pattern Base)？

4. FP-growth算法在什么情况下效率会下降？

5. (可选) 能画一下FP-tree的基本结构吗？

面试实战技巧

相关文章

1. 以后缀 `A` 开始挖掘

步骤 2: 构建条件FP-tree (Conditional FP-tree) for `A`

2. 以后缀 `E` 开始挖掘

步骤 1: 寻找条件模式基 for `E`

步骤 2: 构建条件FP-tree for `E`

步骤 3: 挖掘条件FP-tree for `E``————（看不懂？）末尾有解释`

3. 以后缀 `C` 开始挖掘

步骤 1: 寻找条件模式基 for `C`

步骤 2: 构建条件FP-tree for `C`

步骤 3: 挖掘条件FP-tree for `C`

4. 以后缀 `B` 开始挖掘

步骤 1: 寻找条件模式基 for `B`

步骤 2: 构建条件FP-tree for `B`

步骤 3: 挖掘条件FP-tree for `B`

第二步：处理树上的下一个点 `C`

最终我们找到了所有带 `E` 的宝贝：