1、堆的概念与结构

堆是一种特殊的二叉树，根结点最大的堆称为大根堆（也叫最大堆），根结点最小的堆称为小根堆（也叫最小堆）

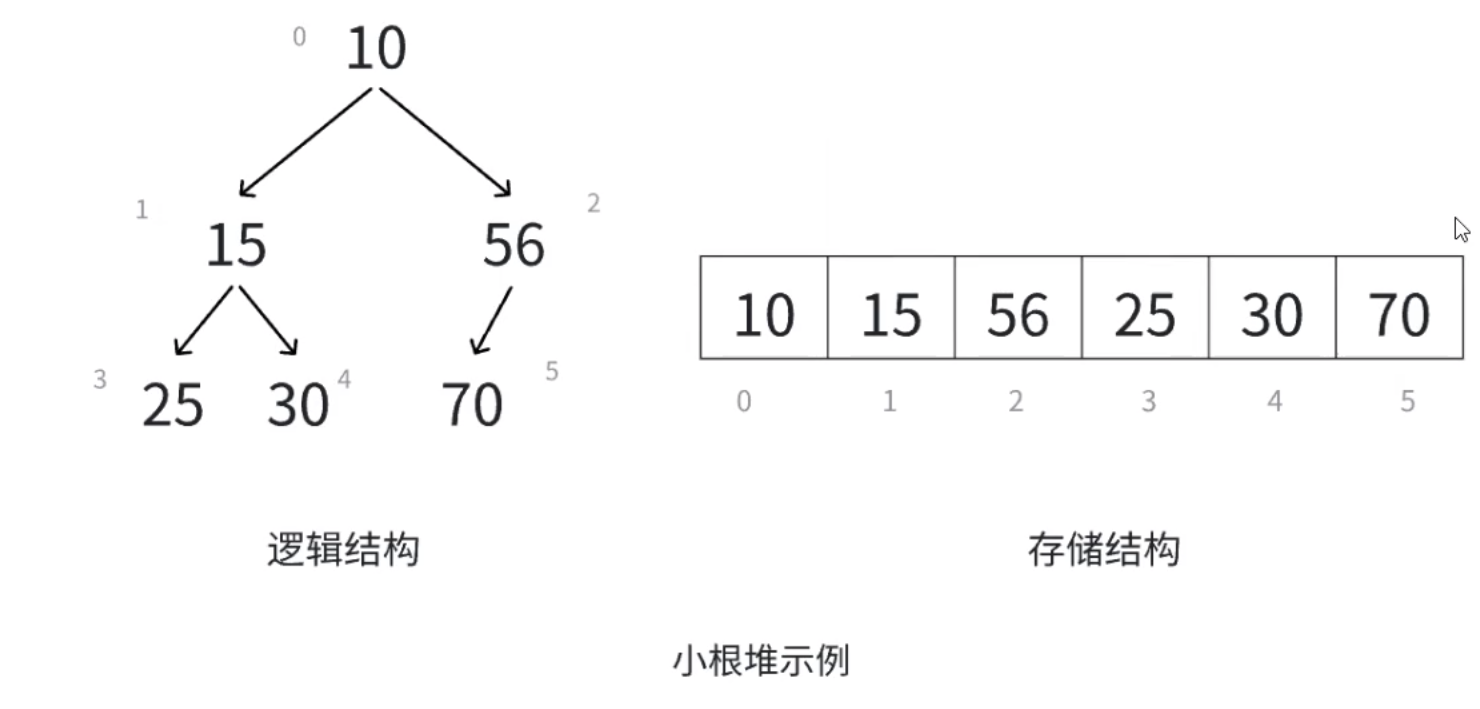
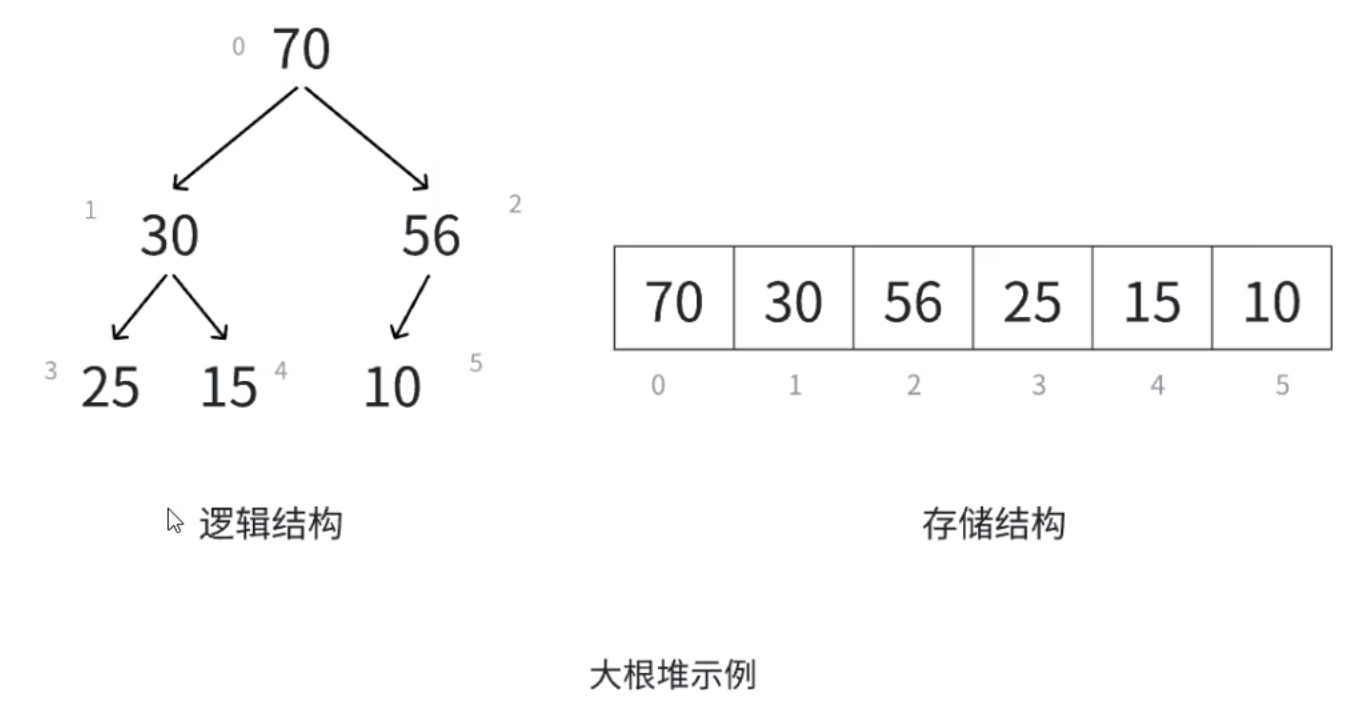
堆具有以下性质：（1）堆中某个结点的值总是不大于或不小于其父结点的值

（2）堆总是一棵完全二叉树

二叉树的性质

对于具有n个结点的完全二叉树，如果从上至下从左至右的数组顺序对所有结点从0开始编号，对于序号为i的结点有：

1. 若 i > 0，i 位置的双亲结点序号：（i - 1）/ 2；i = 0，i 为根结点，无双亲结点

2. 若 2i + 1 < n，左孩子序号：2i + 1，若 2i + 1 >= n，则没有左孩子

3. 若 2i + 1 < n，右孩子序号：2i + 2，若 2i + 2 >= n，则没有右孩子

2、堆的实现

2.1 向上调整算法（堆的插入）

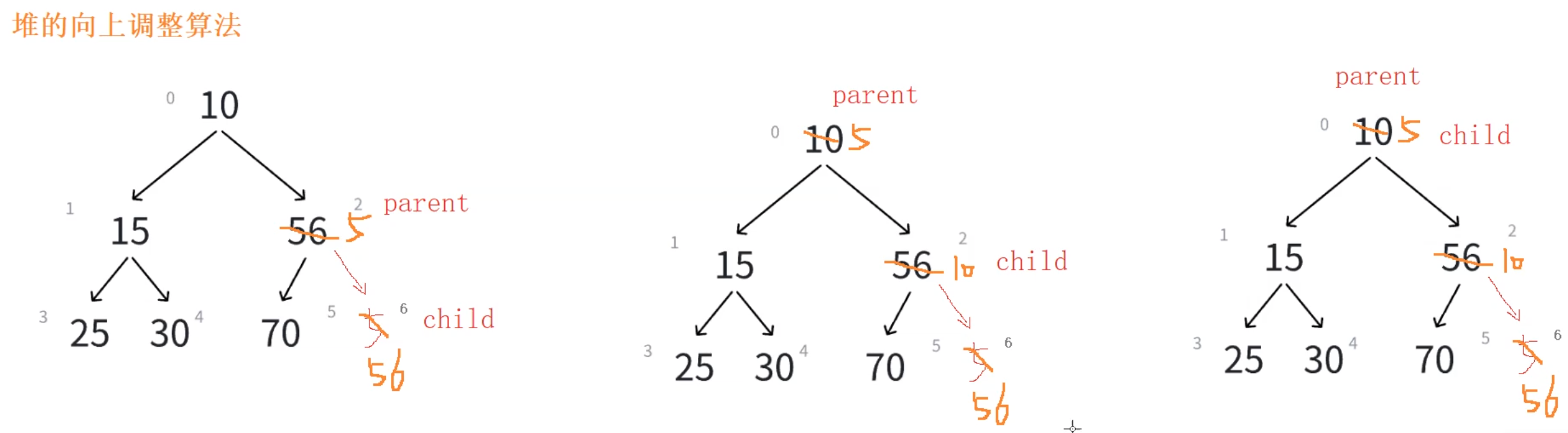
将新数据插入到数组的尾上，再进行向上调整算法，直到满足堆。

向上调整算法

1、先将元素插入到堆的末尾，即最后一个孩子之后

2、插入之后如果堆的性质遭到破坏，将新插入节点顺着其双亲往上调整到合适位置即可

void Swap(HPDataType* x, HPDataType* y)
{HPDataType tmp = *x;*x = *y;*y = tmp;
}void AdjustUp(HPDataType* arr, int child)
{int parent = (child - 1) / 2;while (child > 0){//大堆:         >//小堆:         <if (arr[child] < arr[parent]){//调整Swap(&arr[child], &arr[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}

2.2 向下调整算法（堆的删除）

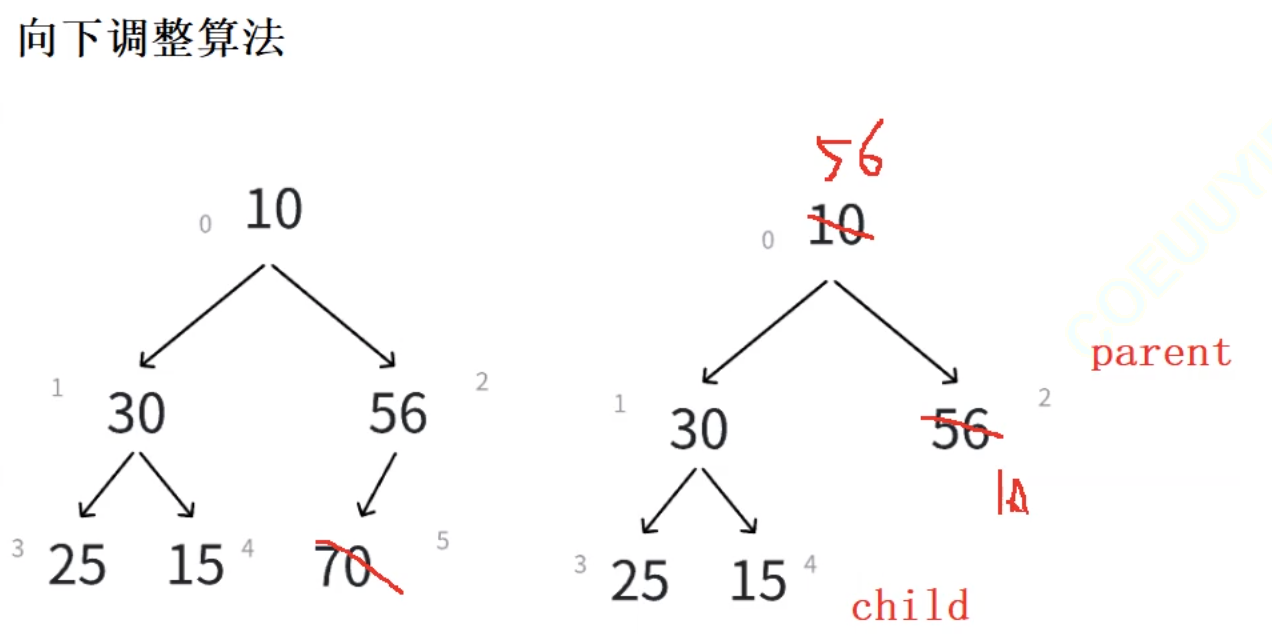
删除堆是删除堆顶的数据，将堆顶数据和最后一个数据交换，然后删除最后一个数据，再进行向下调整算法。

向下调整算法

1、将堆顶元素与堆中最后一个元素进行交换

2、删除堆中最后一个元素

3、将堆顶元素向下调整直到满足堆的特性为止

void AdjustDown(HPDataType* arr, int parent, int n)
{int child = 2 * parent + 1;//左孩子while (child < n){if (child + 1 < n && arr[child] > arr[child + 1]){child = child + 1;}if (arr[child] < arr[parent]){//调整Swap(&arr[child], &arr[parent]);parent = child;child = 2 * child + 1;}else{break;}}
}void HPPop(HP* php)
{assert(!HPEmpty(php));//0   php->size - 1Swap(&php->arr[0], &php->arr[php->size - 1]);php->size--;//向下调整AdjustDown(php->arr, 0, php->size);
}

2.3 完整代码

Heap.h

#pragma once
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
#include <assert.h>//堆的结构
typedef int HPDataType;
typedef struct Heap
{HPDataType* arr;int size;     //有效数据个数int capacity; //空间大小
}HP;void HPInit(HP* php);
void HPDestroy(HP* php);
void HPPrint(HP* php);void HPPush(HP* php, HPDataType x);
void HPPop(HP* php);//判空
bool HPEmpty(HP* php);//取堆顶数据
HPDataType HPTop(HP* php);

Heap.c

#define  _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"void HPInit(HP* php)
{php->arr = NULL;php->size = php->capacity = 0;
}void HPDestroy(HP* php)
{if (php->arr)free(php->arr);php->arr = NULL;php->size = php->capacity = 0;
}void HPPrint(HP* php)
{for (int i = 0;i < php->size;i++){printf("%d ", php->arr[i]);}printf("\n");
}void Swap(HPDataType* x, HPDataType* y)
{HPDataType tmp = *x;*x = *y;*y = tmp;
}void AdjustUp(HPDataType* arr, int child)
{int parent = (child - 1) / 2;while (child > 0){//大堆:         >//小堆:         <if (arr[child] < arr[parent]){//调整Swap(&arr[child], &arr[parent]);child = parent;parent = (parent - 1) / 2;}else{break;}}
}void HPPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : 2 * php->capacity;HPDataType* tmp = (HPDataType*)realloc(php->arr, newCapacity * sizeof(int));if (tmp == NULL){perror("realloc fail!");exit(1);}php->arr = tmp;php->capacity = newCapacity;}php->arr[php->size] = x;//向上调整AdjustUp(php->arr, php->size);php->size++;
}//判空
bool HPEmpty(HP* php)
{assert(php);return php->size == 0;
}void AdjustDown(HPDataType* arr, int parent, int n)
{int child = 2 * parent + 1;//左孩子while (child < n){if (child + 1 < n && arr[child] > arr[child + 1]){child = child + 1;}if (arr[child] < arr[parent]){//调整Swap(&arr[child], &arr[parent]);parent = child;child = 2 * child + 1;}else{break;}}
}void HPPop(HP* php)
{assert(!HPEmpty(php));//0   php->size - 1Swap(&php->arr[0], &php->arr[php->size - 1]);php->size--;//向下调整AdjustDown(php->arr, 0, php->size);
}//取堆顶数据
HPDataType HPTop(HP* php)
{assert(!HPEmpty(php));return php->arr[0];
}

test.c

#define  _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"void test01()
{HP hp;HPInit(&hp);HPPush(&hp, 56);HPPush(&hp, 10);HPPush(&hp, 15);HPPush(&hp, 30);HPPush(&hp, 70);HPPush(&hp, 25);HPPrint(&hp);HPPop(&hp);HPPrint(&hp);HPDestroy(&hp);
}void test02()
{HP hp;HPInit(&hp);HPPush(&hp, 56);HPPush(&hp, 10);HPPush(&hp, 15);HPPush(&hp, 30);HPPrint(&hp);while (!HPEmpty(&hp)){int top = HPTop(&hp);printf("%d ", top);HPPop(&hp);}
}int main()
{//test01();test02();return 0;
}

3、堆的应用

3.1 堆排序

我们发现，依次取出堆顶元素，元素是按照从小到大（或从大到小）的顺序排列输出的，因此，我们可以使用堆这个数据结构来进行排序。

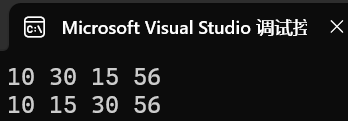
版本一：基于已有数组建堆，取堆顶元素完成排序。

#define  _CRT_SECURE_NO_WARNINGS 1
#include "Heap.h"//堆排序
void HeapSort(int* arr, int n)
{HP hp;HPInit(&hp);for (int i = 0;i < n;i++){HPPush(&hp, arr[i]);}int i = 0;while (!HPEmpty(&hp)){int top = HPTop(&hp);arr[i++] = top;HPPop(&hp);}HPDestroy(&hp);
}int main()
{int arr[6] = { 19,15,20,17,13,10 };HeapSort(arr, 6);for (int i = 0;i < 6;i++){printf("%d ", arr[i]);}printf("\n");return 0;
}

该版本有一个前提，那就是必须要借助堆这个数据结构，而我们所说的堆排序，并不是要用对这个数据结构来排序，而是要借助堆的思想。

版本二：根据数组建堆，首尾交换，交换后的堆尾数据从堆中删掉，将堆顶数据向下调整选出次大的数据。

第一步、根据数组进行建堆

排升序——建大堆

排降序——建小堆

第二步、将堆顶和最后一个数据交换位置，--size并向下调整堆，重复该过程

void HeapSort(int* arr, int n)
{//建堆——向下调整算法建堆for (int i = (n - 1 - 1) / 2;i >= 0;i--){AdjustDown(arr, i, n);}//堆排序int end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdjustDown(arr, 0, end);end--;}
}

向下调整算法建堆时间复杂度为O(n)

void HeapSort(int* arr, int n)
{//建堆——向上调整算法for (int i = 0;i < n;i++){AdjustUp(arr, i);}//堆排序int end = n - 1;while (end > 0){Swap(&arr[0], &arr[end]);AdjustDown(arr, 0, end);end--;}
}

向上调整算法建堆时间复杂度为O(nlogn)

3.2 Top-K问题

Top-K问题：求数据中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。对于Top-K问题，能想到的对简单直接的方式就是排序，最佳的方式就是使用堆排序，基本思路如下：

先取前K个数据建堆，遍历剩下的n - K个数据和堆顶比较。找最大的前K个数据，建小堆，比堆顶数据大就和堆顶元素交换；找最小的前K个数据，建大堆，比堆顶数据小就和堆顶元素交换。

#include "Heap.h"void CreateNData()
{//造数据int n = 100000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen error");return;}for (int i = 0;i < n;i++){int x = (rand() + i) % 100000;fprintf(fin, "%d\n", x);}fclose(fin);
}void TopK()
{printf("请输入k:");int k = 0;scanf("%d", &k);const char* file = "data.txt";FILE* fout = fopen(file, "r");if (fout == NULL){perror("fopen fail");return;}//找最大的前k个数据，建小堆int* minHeap = (int*)malloc(k * sizeof(int));if (minHeap == NULL){perror("malloc fail");return;}for (int i = 0;i < k;i++){fscanf(fout, "%d", &minHeap[i]);}//minHeap--向下调整建堆for (int i = (k - 1 - 1) / 2;i >= 0;i--){AdjustDown(minHeap, i, k);}//遍历剩下的n-k个数据，跟堆顶比较int x = 0;while (fscanf(fout, "%d", &x) != EOF){//minHeap-top    x if (minHeap[0] < x){minHeap[0] = x;AdjustDown(minHeap, 0, k);}}for (int i = 0;i < k;i++){printf("%d ", minHeap[i]);}fclose(fout);
}int main()
{//CreateNData();TopK();return 0;
}