目录

144. 二叉树的前序遍历

94. 二叉树的中序遍历

145. 二叉树的后序遍历

102. 二叉树的层序遍历

226. 翻转二叉树

101. 对称二叉树

104. 二叉树的最大深度

111. 二叉树的最小深度

222. 完全二叉树的节点个数

110. 平衡二叉树

257. 二叉树的所有路径

404. 左叶子之和

513. 找树左下角的值

112. 路径总和

106. 从中序与后序遍历序列构造二叉树

654. 最大二叉树

617. 合并二叉树

700. 二叉搜索树中的搜索

98. 验证二叉搜索树

530. 二叉搜索树的最小绝对差

236. 二叉树的最近公共祖先

235. 二叉搜索树的最近公共祖先

701. 二叉搜索树中的插入操作

450. 删除二叉搜索树中的节点

669. 修剪二叉搜索树

108. 将有序数组转换为二叉搜索树

538. 把二叉搜索树转换为累加树

144. 二叉树的前序遍历

思路

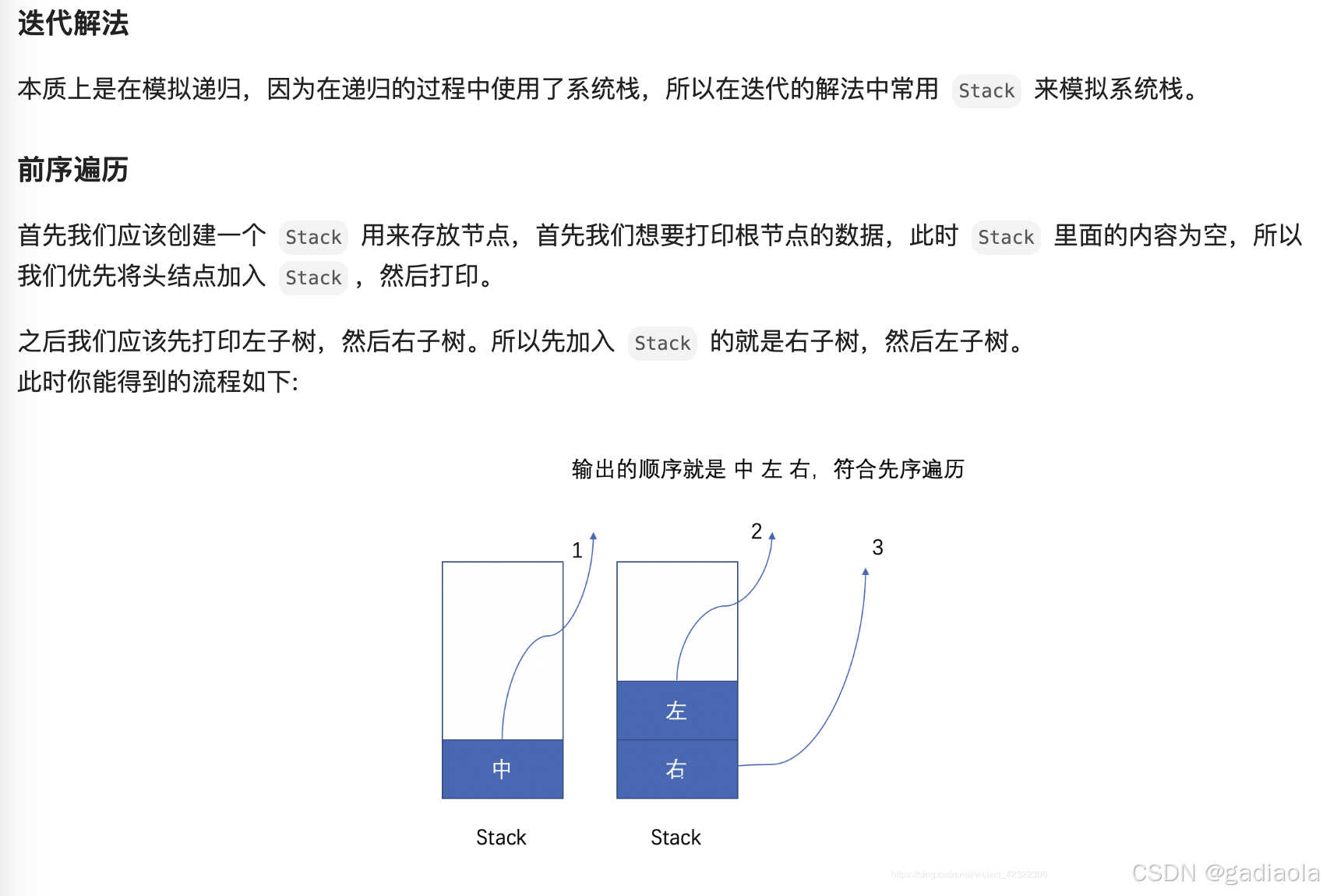
代码（递归）

class Solution {List<Integer> ret = new LinkedList<Integer>();public List<Integer> preorderTraversal(TreeNode root) {preorder(root);return ret;}private void preorder (TreeNode root) {if (root == null) {return;}ret.addLast(root.val);preorder(root.left);preorder(root.right);}
}

代码（迭代）

class Solution {Stack<TreeNode> stack = new Stack<TreeNode>();List<Integer> ret = new LinkedList<Integer>();public List<Integer> preorderTraversal(TreeNode root) {preorder(root);return ret;}private void preorder (TreeNode root) {if (root == null) return;stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.pop();ret.addLast(node.val);if (node.right != null) {stack.push(node.right);}if (node.left != null) {stack.push(node.left);}}}
}

🌟代码（统一迭代法）

class Solution {Stack<TreeNode> stack = new Stack<>();List<Integer> ret = new LinkedList<>();public List<Integer> postorderTraversal(TreeNode root) {if (root != null) stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.peek();if (node != null) {stack.pop();if (node.right != null) stack.push(node.right);if (node.left != null) stack.push(node.left);stack.push(node);stack.push(null);}else {stack.pop();ret.add(stack.pop().val);}}return ret;}
}

94. 二叉树的中序遍历

思路

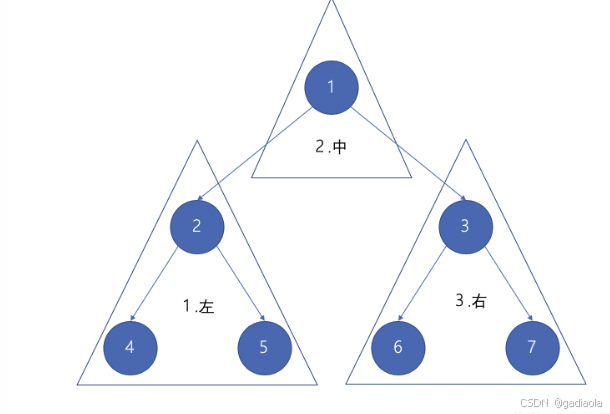
代码（递归）

class Solution {List<Integer> ret = new LinkedList<Integer>();public List<Integer> inorderTraversal(TreeNode root) {inorder(root);return ret;}private void inorder (TreeNode root) {if (root == null) return;inorder(root.left);ret.addLast(root.val);inorder(root.right);}
}

代码（迭代）

class Solution {Stack<TreeNode> stack = new Stack<TreeNode>();List<Integer> ret = new LinkedList<Integer>();public List<Integer> inorderTraversal(TreeNode root) {inorder(root);return ret;}private void inorder (TreeNode root) {if (root == null) return;TreeNode cur = root;while (!stack.isEmpty() || cur != null) {while (cur != null) {stack.push(cur);cur = cur.left;}TreeNode node = stack.pop();ret.addLast(node.val);if (node.right != null) {cur = node.right;}}}
}

🌟代码（统一迭代法）

class Solution {Stack<TreeNode> stack = new Stack<>();List<Integer> ret = new LinkedList<>();public List<Integer> postorderTraversal(TreeNode root) {if (root != null) stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.peek();if (node != null) {stack.pop();if (node.right != null) stack.push(node.right);stack.push(node);stack.push(null);if (node.left != null) stack.push(node.left);}else {stack.pop();ret.add(stack.pop().val);}}return ret;}
}

145. 二叉树的后序遍历

代码（递归）

class Solution {List<Integer> ret = new LinkedList<>();public List<Integer> postorderTraversal(TreeNode root) {postorder(root);return ret;}private void postorder(TreeNode root) {if (root == null) return;postorder(root.left);postorder(root.right);ret.addLast(root.val);}
}

🌟代码（统一迭代法）

class Solution {Stack<TreeNode> stack = new Stack<>();List<Integer> ret = new LinkedList<>();public List<Integer> postorderTraversal(TreeNode root) {if (root != null) stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.peek();if (node != null) {stack.pop();stack.push(node);stack.push(null);if (node.right != null) stack.push(node.right);if (node.left != null) stack.push(node.left);}else {stack.pop();ret.add(stack.pop().val);}}return ret;}
}

102. 二叉树的层序遍历

🌟代码（迭代）

class Solution {Queue<TreeNode> queue = new LinkedList<TreeNode>();List<List<Integer>> ret = new LinkedList<List<Integer>>();public List<List<Integer>> levelOrder(TreeNode root) {lorder(root);return ret;}private void lorder(TreeNode root) {if (root == null) return;queue.offer(root);while (!queue.isEmpty()) {List<Integer> temp = new ArrayList<Integer>();int size = queue.size();while (size > 0) {TreeNode node = queue.poll();temp.add(node.val);if (node.left != null) queue.offer(node.left);if (node.right != null) queue.offer(node.right);size--;}ret.add(temp);}}
}

代码（递归）

class Solution {List<List<Integer>> ret = new LinkedList<List<Integer>>();public List<List<Integer>> levelOrder(TreeNode root) {lorder(root,0);return ret;}private void lorder(TreeNode root,int deep) {if (root == null) return;deep++;if (ret.size() < deep) {List<Integer> temp = new ArrayList<Integer>();ret.add(temp);}ret.get(deep - 1).add(root.val);lorder(root.left,deep);lorder(root.right,deep);}
}

226. 翻转二叉树

代码

class Solution {public TreeNode invertTree(TreeNode root) {postOrder(root);return root;}private void postOrder(TreeNode root) {if (root == null) return;postOrder(root.left);postOrder(root.right);if (root.left != null || root.right != null) {TreeNode temp = root.left;root.left = root.right;root.right = temp;}}
}

代码（官方）

class Solution {public TreeNode invertTree(TreeNode root) {if (root == null) {return null;}TreeNode left = invertTree(root.left); // 翻转左子树TreeNode right = invertTree(root.right); // 翻转右子树root.left = right; // 交换左右儿子root.right = left;return root;}
}

101. 对称二叉树

思路

代码

class Solution {public boolean isSymmetric(TreeNode root) {return check(root.left,root.right);}   private boolean check(TreeNode left ,TreeNode right) {if (left == null && right == null) return true;if (left ==null || right == null) return false;return left.val == right.val && check(left.left,right.right) && check(left.right,right.left);}
}

104. 二叉树的最大深度

代码

class Solution {public int maxDepth(TreeNode root) {if (root == null) return 0;return Math.max(maxDepth(root.left),maxDepth(root.right)) + 1;}
}

111. 二叉树的最小深度

代码

class Solution {public int minDepth(TreeNode root) {if (root == null) return 0;int left = minDepth(root.left);int right = minDepth(root.right);if (root.left != null && root.right == null) return 1 + left;if (root.right != null && root.left == null) return 1 + right;return 1 + Math.min(left,right);}
}

代码（官方）

class Solution {public int minDepth(TreeNode root) {if(root == null) return 0;//这道题递归条件里分为三种情况//1.左孩子和有孩子都为空的情况，说明到达了叶子节点，直接返回1即可if(root.left == null && root.right == null) return 1;//2.如果左孩子和由孩子其中一个为空，那么需要返回比较大的那个孩子的深度        int m1 = minDepth(root.left);int m2 = minDepth(root.right);//这里其中一个节点为空，说明m1和m2有一个必然为0，所以可以返回m1 + m2 + 1;if(root.left == null || root.right == null) return m1 + m2 + 1;//3.最后一种情况，也就是左右孩子都不为空，返回最小深度+1即可return Math.min(m1,m2) + 1; }
}

222. 完全二叉树的节点个数

代码

class Solution {public int countNodes(TreeNode root) {if (root == null) return 0;int left = countNodes(root.left);int right = countNodes(root.right);return 1 + left + right;}
}



110. 平衡二叉树

代码

class Solution {public boolean isBalanced(TreeNode root) {if (root == null) return true;boolean leftbool = isBalanced(root.left);boolean rightbool = isBalanced(root.right);int left = getDepth(root.left);int right = getDepth(root.right);if (Math.abs(left-right) > 1) return false;return leftbool == true && rightbool == true ? true : false;}private int getDepth (TreeNode root) {if (root == null) return 0;return 1 + Math.max(getDepth(root.left),getDepth(root.right));}
}

257. 二叉树的所有路径

代码

class Solution {StringBuilder s = new StringBuilder();List<String> ret = new ArrayList<String>();public List<String> binaryTreePaths(TreeNode root) {order(root,"",ret);return ret;}private void order (TreeNode root,String path,List<String> ret) {if (root == null) return;if (root.left == null && root.right == null) {ret.add(path + root.val);return;}order(root.left,path + root.val + "->",ret);order(root.right,path + root.val + "->",ret);}
}

代码（官方）

    public List<String> binaryTreePaths(TreeNode root) {List<String> res = new ArrayList<>();dfs(root, "", res);return res;}private void dfs(TreeNode root, String path, List<String> res) {//如果为空，直接返回if (root == null)return;//如果是叶子节点，说明找到了一条路径，把它加入到res中if (root.left == null && root.right == null) {res.add(path + root.val);return;}//如果不是叶子节点，在分别遍历他的左右子节点dfs(root.left, path + root.val + "->", res);dfs(root.right, path + root.val + "->", res);}

404. 左叶子之和

代码

class Solution {int sum = 0;public int sumOfLeftLeaves(TreeNode root) {order(root);return sum;}private void order(TreeNode root) {if (root == null) return;if (root.left !=null && root.left.left == null && root.left.right == null) {sum += root.left.val; }order(root.left);order(root.right);}
}

513. 找树左下角的值

代码

class Solution {Queue<TreeNode> queue = new LinkedList<TreeNode>();int lever = 0;public int findBottomLeftValue(TreeNode root) {int high = getHigh(root);if (root == null) return 0;queue.offer(root);while (!queue.isEmpty()) {List<Integer> list = new LinkedList<Integer>();int size = queue.size();while (size > 0) {TreeNode node = queue.poll();list.add(node.val);if (node.left != null) queue.offer(node.left);if (node.right != null) queue.offer(node.right);size--;}lever++;if (lever == high) return list.getFirst();}return 0;}private int getHigh (TreeNode root) {if (root == null) return 0;return 1 + Math.max(getHigh(root.left),getHigh(root.right));}
}

代码（官方）（层序遍历，只不断更新每一层的第一个节点的值）

//迭代法
class Solution {public int findBottomLeftValue(TreeNode root) {if (root == null) return 0;int ret = 0;Queue<TreeNode> que = new LinkedList<TreeNode>();que.offer(root);while (!que.isEmpty()) {int size = que.size();for (int i = 0; i < size;i++) {TreeNode node = que.poll();if (i == 0) ret = node.val;if (node.left != null) que.offer(node.left);if (node.right != null) que.offer(node.right);}}return ret;}
}

112. 路径总和

代码

class Solution {public boolean hasPathSum(TreeNode root, int targetSum) {if (root == null) return false;if (root.left == null && root.right == null) {return targetSum == root.val;}return hasPathSum(root.left,targetSum - root.val) || hasPathSum(root.right,targetSum - root.val);        }
}

106. 从中序与后序遍历序列构造二叉树

代码

class Solution {public TreeNode buildTree(int[] inorder, int[] postorder) {if(postorder.length == 0 || inorder.length == 0)return null;return buildHelper(inorder, 0, inorder.length, postorder, 0, postorder.length);}private TreeNode buildHelper(int[] inorder, int inorderStart, int inorderEnd, int[] postorder, int postorderStart, int postorderEnd){if(postorderStart == postorderEnd)return null;int rootVal = postorder[postorderEnd - 1];TreeNode root = new TreeNode(rootVal);int middleIndex;for (middleIndex = inorderStart; middleIndex < inorderEnd; middleIndex++){if(inorder[middleIndex] == rootVal)break;}int leftInorderStart = inorderStart; int leftInorderEnd = middleIndex;int rightInorderStart = middleIndex + 1;int rightInorderEnd = inorderEnd;int leftPostorderStart = postorderStart;int leftPostorderEnd = postorderStart + (middleIndex - inorderStart);int rightPostorderStart = leftPostorderEnd;int rightPostorderEnd = postorderEnd - 1;root.left = buildHelper(inorder, leftInorderStart, leftInorderEnd,  postorder, leftPostorderStart, leftPostorderEnd);root.right = buildHelper(inorder, rightInorderStart, rightInorderEnd, postorder, rightPostorderStart, rightPostorderEnd);return root;}  
}

654. 最大二叉树

代码

class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {if (nums.length == 0) return null;int max = 0;int index = 0;for (int i = 0; i < nums.length;i++) {if (nums[i] > max) {max = nums[i];index = i;}}TreeNode root = new TreeNode(max);TreeNode left = constructMaximumBinaryTree(Arrays.copyOfRange(nums,0,index));TreeNode right = constructMaximumBinaryTree(Arrays.copyOfRange(nums,index + 1,nums.length));root.left = left;root.right = right;return root;}
}

617. 合并二叉树

题解

class Solution {public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {if (root1 == null && root2 == null) return null;if (root1 != null && root2 == null) {return root1;}if (root1 == null && root2 != null) {return root2;}TreeNode node = new TreeNode(root1.val + root2.val);TreeNode left = mergeTrees(root1.left,root2.left);TreeNode right = mergeTrees(root1.right,root2.right);node.left = left;node.right = right;return node;}
}

700. 二叉搜索树中的搜索

代码

class Solution {public TreeNode searchBST(TreeNode root, int val) {if (root == null) return null;if (root.val == val) return root;if (root.val < val) {return searchBST(root.right,val);}return searchBST(root.left,val);}
}

98. 验证二叉搜索树

代码

class Solution {public boolean isValidBST(TreeNode root) {if (root == null) return true;if (root.left != null) {TreeNode p = root.left;while (p.right != null) {p = p.right;}if (p.val >= root.val) return false;}if (root.right != null) {TreeNode p = root.right;while (p.left != null) {p = p.left;}if (p.val <= root.val) return false;}boolean left = isValidBST(root.left);boolean right = isValidBST(root.right);return left && right;}
}

530. 二叉搜索树的最小绝对差

代码

class Solution {int ret = Integer.MAX_VALUE;public int getMinimumDifference(TreeNode root) {order(root);return ret;}public void order (TreeNode root) {if (root == null) return;if (root.left != null) {TreeNode p = root.left;while (p.right != null) {p = p.right;}ret = Math.min(ret,root.val - p.val);}if (root.right != null) {TreeNode p = root.right;while (p.left != null) {p = p.left;}ret = Math.min(ret,p.val - root.val);}order(root.left);order(root.right);}
}

236. 二叉树的最近公共祖先

代码

class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if (root.val == p.val || root.val == q.val) return root;if (root.right == null || order(root.left,p) && order(root.left,q)) {return lowestCommonAncestor(root.left,p,q);}if (root.left == null || order(root.right,p) && order(root.right,q)) {return lowestCommonAncestor(root.right,p,q);}return root;}public boolean order (TreeNode root,TreeNode node) {if (root == null) return false;if (root.val == node.val) return true;return order(root.left,node) || order(root.right,node);}
}

235. 二叉搜索树的最近公共祖先

代码

class Solution {public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if (root.val < p.val && root.val < q.val) {return lowestCommonAncestor(root.right,p,q);}if (root.val > p.val && root.val > q.val) {return lowestCommonAncestor(root.left,p,q);}return root;}
}

701. 二叉搜索树中的插入操作

代码

class Solution {public TreeNode insertIntoBST(TreeNode root, int val) {if (root == null) {TreeNode node = new TreeNode(val);return node;}order(root,val);return root;}public void order (TreeNode root,int val) {if (root.val < val) {if (root.right == null) {TreeNode node = new TreeNode(val);root.right = node;}insertIntoBST(root.right,val);}if (root.val > val) {if (root.left == null) {TreeNode node = new TreeNode(val);root.left = node;}insertIntoBST(root.left,val);}}
}

450. 删除二叉搜索树中的节点

代码

class Solution {public TreeNode deleteNode(TreeNode root, int key) {if (root == null) return null;// 根据值的大小递归调整左右子树if (key < root.val) {root.left = deleteNode(root.left, key);} else if (key > root.val) {root.right = deleteNode(root.right, key);} else {// 找到待删除节点if (root.left == null) return root.right;  // 无左子树，返回右子树if (root.right == null) return root.left;  // 无右子树，返回左子树// 有两个子树：找到右子树的最小节点TreeNode minNode = findMin(root.right);root.val = minNode.val;root.right = deleteNode(root.right, minNode.val); // 递归删除替换节点}return root;}private TreeNode findMin(TreeNode node) {while (node.left != null) node = node.left;return node;}
}

669. 修剪二叉搜索树

代码

class Solution {public TreeNode trimBST(TreeNode root, int low, int high) {if (root == null) {return null;}if (root.val < low) {return trimBST(root.right, low, high);}if (root.val > high) {return trimBST(root.left, low, high);}// 当前节点值在范围内，递归处理左右子树root.left = trimBST(root.left, low, high);root.right = trimBST(root.right, low, high);return root;}
}

108. 将有序数组转换为二叉搜索树

代码

class Solution {public TreeNode sortedArrayToBST(int[] nums) {if (nums.length == 0) return null;int index = nums.length / 2;int n = nums.length;TreeNode node = new TreeNode(nums[index]);node.left = sortedArrayToBST(Arrays.copyOfRange(nums,0,index));node.right = sortedArrayToBST(Arrays.copyOfRange(nums,index + 1,n));return node;}
}

538. 把二叉搜索树转换为累加树

代码

class Solution {public TreeNode convertBST(TreeNode root) {if (root == null) return null;TreeNode right = convertBST(root.right);if (root.right !=  null) {TreeNode node = root.right;while (node.left != null) {node = node.left;}root.val += node.val;}if (root.left != null) {TreeNode node = root.left;while (node.right != null) {node = node.right;}node.val += root.val;}TreeNode left = convertBST(root.left);root.left = left;root.right = right;return root;}
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若转载，请注明出处：http://www.pswp.cn/bicheng/91481.shtml
繁体地址，请注明出处：http://hk.pswp.cn/bicheng/91481.shtml
英文地址，请注明出处：http://en.pswp.cn/bicheng/91481.shtml

如若内容造成侵权/违法违规/事实不符，请联系英文站点网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

基于deepseek的文本解析 - 超长文本的md结构化

基于deepseek的文本解析 - 超长文本的md结构化

pdf超长合同或其他超100页非结构化文档&#xff0c;很难全量提交deepseek进行分析&#xff0c;一般需要先进行分割。然而&#xff0c;不管是langchain还是llamaindex提供的文本分割工具&#xff0c;很难直接对非结构化文本进行准确的内容分割&#xff0c;很多原始整体段落被划分…
阅读更多...
介绍一个图像修复开源项目，从模糊到清晰仅需1.7秒：HYPIR图像修复技术如何改变数字世界？

介绍一个图像修复开源项目，从模糊到清晰仅需1.7秒：HYPIR图像修复技术如何改变数字世界？

文章概要 作为一名长期关注图像处理技术的爱好者&#xff0c;当我第一次接触到HYPIR这一革命性图像修复工具时&#xff0c;我被其惊人的速度和质量所震撼。本文将全面介绍由中国科学院深圳先进技术研究院董超研究员团队研发的HYPIR图像修复大模型&#xff0c;详细解析其核心技术…
阅读更多...
基于UDP的SNMP协议

基于UDP的SNMP协议

SNMP协议详解 SNMP (Simple Network Management Protocol)&#xff0c;“简单网络管理协议”&#xff0c;是广泛应用于TCP/IP网络中&#xff0c;用于管理和监控网络设备的一种标准协议。它允许网络管理员查询网络设备的状态信息、配置参数、接收故障告警等&#xff0c;从而实现…
阅读更多...
3D空间中的变换矩阵

3D空间中的变换矩阵

3D 空间中的变换矩阵详解 在 3D 计算机图形学中&#xff0c;所有几何变换都可以通过 44 齐次变换矩阵 来表示。以下详细介绍各种变换矩阵及其原理。 核心变换矩阵 1. 单位矩阵&#xff08;不变变换&#xff09; I[1000010000100001] I \begin{bmatrix} 1 & 0 & 0 &…
阅读更多...
长连接（Long Connection）详解

长连接（Long Connection）详解

一、长连接基本概念长连接&#xff08;也称为持久连接&#xff09;是指在一个TCP连接上可以连续发送多个HTTP请求/响应&#xff0c;而不是每次通信都建立新的连接。这是HTTP/1.1的默认行为&#xff0c;通过Connection: keep-alive头部实现。二、工作原理1. 传统短连接流程客户端…
阅读更多...
【汇总】接口自动化测试 + 持续集成（文末视频演示）

【汇总】接口自动化测试 + 持续集成（文末视频演示）

技术栈&#xff1a;java testng httpclient allure fastjson jsonpath poi/yaml log4j 有建议请联系wx&#xff1a;ren168632201 java接口自动化系列(01)&#xff1a;自动化测试框架设计(入门版) java接口自动化系列(02)&#xff1a;测试数据文件设计(excel/yam) java接…
阅读更多...
科研快报 |无人机+AI：广东防控基孔热背后的技术革命

科研快报 |无人机+AI：广东防控基孔热背后的技术革命

Prism Path 科 研 快 报 CS跨学科顶尖期刊论文资讯 -NO.2025001- 人工智能在登革热预防、控制与管理中的作用&#xff1a;一项技术性叙述综述 The role of artificial intelligence for dengue prevention, control, and management: A technical narrative review 期刊…
阅读更多...
常见的中间件漏洞

常见的中间件漏洞

建议&#xff1a;启动下一个环境时&#xff0c;将上一个环境关闭&#xff0c;防止端口冲突和运行卡顿1.TomcatTomcat put方法任意文件写入漏洞Apache Tomcat 7.0.0 - 7.0.79 Apache Tomcat 8.5.19环境&#xff1a;cd vulhub-master/tomcat/CVE-2017-12615 docker-compose up -d…
阅读更多...
7寸工业模组 XA070Y2-L01芯显科技详细参数资料

7寸工业模组 XA070Y2-L01芯显科技详细参数资料

芯显7寸工业液晶屏 XA070Y2-L01 技术规格单 基础信息 项目 参数 制造商 芯显 型号 XA070Y2-L01 显示技术 a-Si TN TFT-LCD 应用场景 车载中控 / 工业HMI 屏幕尺寸 7.0英寸 机械结构 特性 指标 显示区域 152.4 91.44 mm 整机尺寸 165 104.09 9.1 mm 公差范围 0.5 mm 表面处理…
阅读更多...
机器学习基础-numpy

机器学习基础-numpy

一、相关知识点二、例子&#xff1a;import matplotlib.pyplot as plt import numpy as npplt.rcParams[font.sans-serif] [KaiTi] # 使用黑体 plt.rcParams[axes.unicode_minus] False # 解决负号显示问题math np.random.randint(low60,high100,size50) english np.rand…
阅读更多...
Cockpit管理服务器

Cockpit管理服务器

Cockpit 是一个开源工具&#xff0c;通过Web Console管理Linux服务器。部署 Cockpit[rootserver ~ 11:05:26]# yum -y install cockpit​[rootserver ~ 11:30:26]# systemctl enable cockpit.socket --nowCreated symlink from /etc/systemd/system/sockets.target.wants/cockp…
阅读更多...
处理订单过期但支付成功的系统设计：平衡用户体验与业务规则

处理订单过期但支付成功的系统设计：平衡用户体验与业务规则

设计一个处理订单过期但用户支付成功的场景&#xff0c;需要平衡用户体验、系统一致性和业务规则。以下是一个系统化的设计方案&#xff0c;涵盖关键流程、异常处理和用户沟通&#xff1a;1. 场景分析 背景&#xff1a;用户在下单后&#xff0c;订单因超时而被标记为“过期”&a…
阅读更多...
AI学习笔记三十三：基于Opencv的单目标跟踪

AI学习笔记三十三：基于Opencv的单目标跟踪

若该文为原创文章&#xff0c;转载请注明原文出处。一、功能介绍主要是想实现跟踪视频中的一个特定目标。使用了OpenCV库来实现视频中特定目标的跟踪。需要提供视频文件路径以及目标在第一帧中的位置坐标&#xff08;x, y, width, height&#xff09;&#xff0c;程序会自动跟踪…
阅读更多...
第二篇：Three.js核心三要素：场景、相机、渲染器

第二篇：Three.js核心三要素：场景、相机、渲染器

第二篇&#xff1a;Three.js核心三要素&#xff1a;场景、相机、渲染器 引言 在Three.js的世界里&#xff0c;场景(Scene)、相机(Camera)和渲染器(Renderer)构成了最基础的"铁三角"。它们如同导演、摄像机和放映机&#xff0c;共同决定了3D内容的呈现方式。本篇将深入…
阅读更多...
RagFlow本地源码部署(非Docker)

RagFlow本地源码部署(非Docker)

参考官方文档做个总结 1. 提前安装好uv pipx install uv pre-commit2. 下载源码&#xff1a; git clone https://github.com/infiniflow/ragflow.git cd ragflow/ uv sync --python 3.10 --all-extras # install RAGFlow dependent python modules uv run download_deps.py …
阅读更多...
[免费]基于Python的招聘职位信息推荐系统(猎聘网数据分析与可视化)(Django+requests库)【论文+源码+SQL脚本】

[免费]基于Python的招聘职位信息推荐系统(猎聘网数据分析与可视化)(Django+requests库)【论文+源码+SQL脚本】

大家好&#xff0c;我是python222_小锋老师&#xff0c;看到一个不错的基于Python的招聘职位信息推荐系统(猎聘网数据分析与可视化)(Djangorequests库)&#xff0c;分享下哈。 项目视频演示 【免费】基于Python的招聘职位信息推荐系统(猎聘网数据分析与可视化)(Django爬虫) P…
阅读更多...
国产化PDF处理控件Spire.PDF教程：Java 提取 PDF 图片，高质量提取与图片过滤技巧

国产化PDF处理控件Spire.PDF教程：Java 提取 PDF 图片，高质量提取与图片过滤技巧

在处理包含图片的 PDF 文件时&#xff0c;例如扫描文档、产品手册或宣传资料&#xff0c;我们经常需要将其中的图像提取出来&#xff0c;用于保存、识别或再加工。E-iceblue旗下Spire系列产品&#xff0c;是文档处理领域的佼佼者&#xff0c;支持国产化信创。本文将介绍如何使用…
阅读更多...
Cesium 快速入门（七）材质详解

Cesium 快速入门（七）材质详解

Cesium 快速入门&#xff08;七&#xff09;材质详解 看过的知识不等于学会。唯有用心总结、系统记录&#xff0c;并通过温故知新反复实践&#xff0c;才能真正掌握一二 作为一名摸爬滚打三年的前端开发&#xff0c;开源社区给了我饭碗&#xff0c;我也将所学的知识体系回馈给大…
阅读更多...
C++：结构体（Structure）

C++：结构体（Structure）

目录 第一性原理出发&#xff1a;我们要解决什么问题&#xff1f; 定义结构体&#xff08;Defining Structures&#xff09; 问题&#xff1a;名字太长怎么办&#xff1f; 如何定义结构体变量&#xff1f; 结构体的大小&#xff08;Size of Structures&#xff09; 初始化…
阅读更多...
化学结构式解读指南：从基础认知到InDraw智能识别

化学结构式解读指南：从基础认知到InDraw智能识别

中文名称&#xff1a;3-[2-(二甲基氨基)乙基]-1H-吲哚英文名称&#xff1a;3-[2-(dimethylamino)ethyl]-1H-indole分子式: C12H16N2分子量: 188.2740这是什么结构式&#xff1f;怎么绘制呢&#xff1f;可以用InDraw里的AI图像识别这个结构式&#xff0c;也可以手动绘图&#xf…
阅读更多...
最新文章

Copyright @ 2022~2023