一、子空间投影
1.1 投影与误差
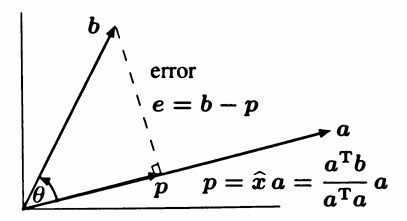
向量b 在 向量a 上的投影即 a 上离 b 最近的点:
p=aTbaTaa
p = \frac{a^T b}{a^Ta}a
p=aTaaTba
我们记 误差 e = b - p,显然误差e 和 a 是正交的。
1.2 投影矩阵
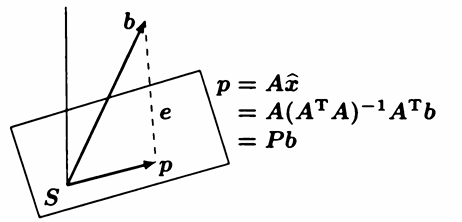
向量b 在子空间S上的投影是S中离b 最近的向量p。
我们做如下推导:
记子空间S=C(A),p为b在S上投影因为p∈C(A),故Ax^=p有解e=b−p=b−Ax^,e和C(A)正交则AT(b−Ax^)=Ae=0,(亦即:e⊥C(A),e∈N(AT))打开括号:ATAx^=ATb假定ATA可逆,则有:x^=(ATA)−1ATbAx^=p=A(ATA)−1ATb
\begin{align}
& 记子空间S = C(A),p 为 b 在S 上投影\\
& 因为p \in C(A), 故 A\hat x= p 有解 \\
& e = b - p = b - A\hat x, e 和 C(A) 正交 \\
& 则 A^T (b-A\hat x) = Ae = 0 ,(亦即:e\perp C(A), e \in N(A^T))\\
& 打开括号:A^TA \hat x=A^Tb \\
& 假定 A^TA 可逆,则有:\\
& \hat x = (A^TA)^{-1}A^Tb \\
& A \hat x = p = A(A^TA)^{-1}A^T b
\end{align}
记子空间S=C(A),p为b在S上投影因为p∈C(A),故Ax^=p有解e=b−p=b−Ax^,e和C(A)正交则AT(b−Ax^)=Ae=0,(亦即:e⊥C(A),e∈N(AT))打开括号:ATAx^=ATb假定ATA可逆,则有:x^=(ATA)−1ATbAx^=p=A(ATA)−1ATb
也就是说 A(ATA)−1ATA(A^TA)^{-1}A^TA(ATA)−1AT 这个矩阵把 向量b 投影到了子空间S上。
我们称列空间 C(A) 上的投影矩阵为P=A(ATA)−1ATP = A(A^TA)^{-1}A^TP=A(ATA)−1AT。
事实上,P=A(ATA)−1AT可分为如下几种情况:case1:A是可逆方阵,则P=A(ATA)−1AT=AA−1(AT)−1AT=I此时,b∈C(A),e=0,b=pcase2:A不是方阵,则我们不能拆开(ATA)−1更为重要的是,ATA是可逆的,当且仅当A的列向量线性无关证明:不妨设A是m行n列则n=r(ATA)≤r(A)≤n则A的列向量线性无关,证毕
\begin{align}
& 事实上,P = A(A^TA)^{-1}A^T 可分为如下几种情况:\\ \\
& case1:A是可逆方阵,则 P = A(A^TA)^{-1}A^T = AA^{-1}(A^T)^{-1}A^T = I\\
& 此时,b \in C(A),e = 0,b=p\\ \\
& case2:A 不是方阵,则 我们不能拆开 (A^TA)^{-1} \\
& 更为重要的是,A^TA 是可逆的,当且仅当 A 的列向量线性无关 \\ \\
& 证明:不妨设 A 是 m行n列 \\
& 则 n = r(A^TA) \le r(A) \le n \\
& 则 A 的列向量线性无关,证毕
\end{align}
事实上,P=A(ATA)−1AT可分为如下几种情况:case1:A是可逆方阵,则P=A(ATA)−1AT=AA−1(AT)−1AT=I此时,b∈C(A),e=0,b=pcase2:A不是方阵,则我们不能拆开(ATA)−1更为重要的是,ATA是可逆的,当且仅当A的列向量线性无关证明:不妨设A是m行n列则n=r(ATA)≤r(A)≤n则A的列向量线性无关,证毕
当A的列向量线性无关时,我们可以得出如下结论:
- P 是对称阵
- $ P^2 = P$
- ATAx=ATbA^TAx = A^TbATAx=ATb 一定有解
1.3 A 列向量线性相关的情况
当 A 列向量线性相关时,我们不能使用投影矩阵公式,如何做投影?
对 A 列变换高斯消元找到一组基向量,记基向量构成的矩阵A’
则有投影矩阵 P=A′((A′)TA′)−1(A′)TP=A'((A')^TA')^{−1}(A')^TP=A′((A′)TA′)−1(A′)T
二、最小二乘法
通过 一的内容 我们知道,ATAx^=ATbA^TA \hat x = A^T bATAx^=ATb 给出了 b 在 C(A) 上的投影 p=Ax^p = A\hat xp=Ax^
当 Ax = b 无解时,我们称 x^\hat xx^ 是 最小二乘解(least-squares solution)。
- 它满足 ∣Ax^−b∣2|A\hat x - b|^2∣Ax^−b∣2 最小,即误差最小
最小二乘法的一个重要应用就是直线拟合。
- 给定m 个点,求出一条直线使得:Σe 最小,即误差和最小
这里不做过多介绍。

















(表结构的操作、数据类型、约束))

