算法	相关知识点	可以通过点击	以下链接进行学习	一起加油！

动态规划是一种解决最优化问题的强大技术，通过将问题分解为子问题并逐步求解来实现高效计算。斐波那契数列是动态规划中经典的应用之一，其递推关系非常适合用动态规划进行优化。通过动态规划，我们不仅能避免重复计算，从而大幅提高计算效率，还能直观地理解递推模型在实际问题中的应用。本文将带你深入理解斐波那契数列的递推模型，展示如何利用动态规划来优化其计算过程，并探讨这一方法的实际价值与应用。

🌈个人主页：是店小二呀
🌈C/C++专栏：C语言\ C++
🌈初/高阶数据结构专栏： 初阶数据结构\ 高阶数据结构
🌈Linux专栏： Linux
🌈算法专栏：算法
🌈Mysql专栏:Mysql

🌈你可知:无人扶我青云志 我自踏雪至山巅

动态规划前言介绍

动态规划（Dynamic Programming, DP）是一种解决最优化问题的方法，它将复杂问题拆解成多个简单的子问题，通过保存子问题的解来避免重复计算，从而提高计算效率。

动态规划适用于具有重叠子问题和最优子结构的场景：

1. 重叠子问题：问题可以被分解成相同的子问题，且子问题会重复计算。通过存储这些子问题的解，可以避免重复计算，节省时间。
2. 最优子结构：问题的最优解可以通过其子问题的最优解来构建，即最优解是由子问题的最优解组合而成。

【动态规划的基本思路】：

1. 状态表示

• 这一部分是指DP表里面的值所表达的含义。通常可以从以下三个角度来确定：
  1. 题目要求：从题目的要求来定义状态。
  2. 经验 + 题目要求：结合经验和题目要求确定状态。
  3. 分析问题的过程中，发现重复子问题：在分析问题时，可以发现哪些是重复的子问题，进而决定状态的定义。

2. 状态转移方程

• 状态转移方程描述了当前状态如何由前一个或多个状态推导出来。例如，dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]，这表示当前状态是由前几个状态的值组合而成的。

3. 初始化

• 设置初始状态，以确保在填表时不会越界。比如，对于斐波那契数列，dp[0]和dp[1]可能需要提前设定为已知的初始值。

4. 顺序计算

• 在填充状态表时，必须保证填充当前状态时，所依赖的先前状态已经计算出来。这通常意味着需要按照一定的顺序（例如，从小到大）来计算状态。

5. 返回值

• 根据题目要求，返回最终的状态值。例如，如果我们计算的是最短路径、最大值或最优解，返回的是状态表中相应位置的值。

---

1137第 N 个泰波那契数

【题目】：1137. 第 N 个泰波那契数

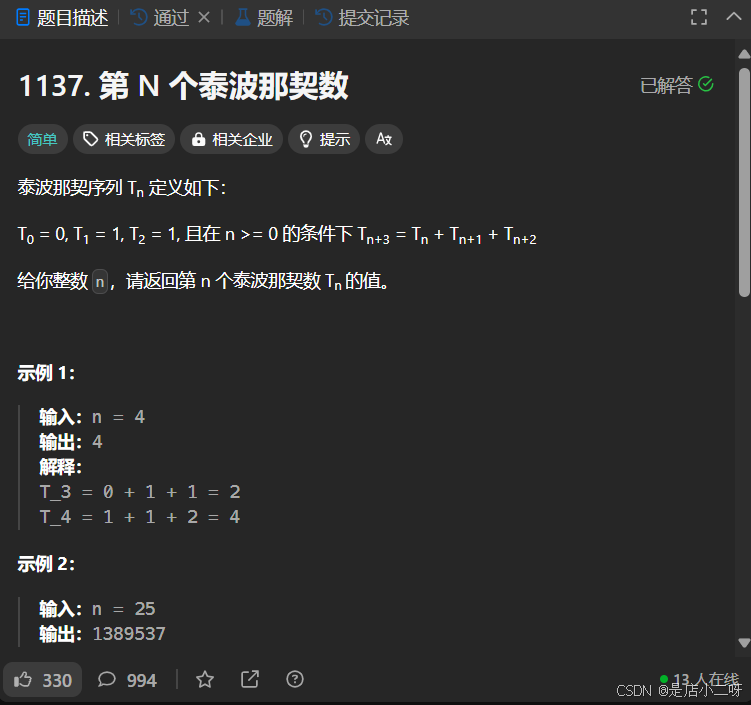
【算法思路】

这道题典型地使用动态规划（DP）来快速计算所需元素，流程如下：

1. 创建 DP 表
2. 初始化
3. 填表
4. 返回结果

【代码实现】

class Solution {
public:int tribonacci(int n) {if(n == 0) return 0;if(n == 1 || n == 2) return 1;vector<int> dp(n + 1);dp[0] = 0;dp[1] = dp[2] = 1;for(int i = 3; i <= n; i++)dp[i] = dp[i - 1] + dp[i - 2] + dp[ i- 3];return dp[n];}
};

【优化方案】：滚动数组

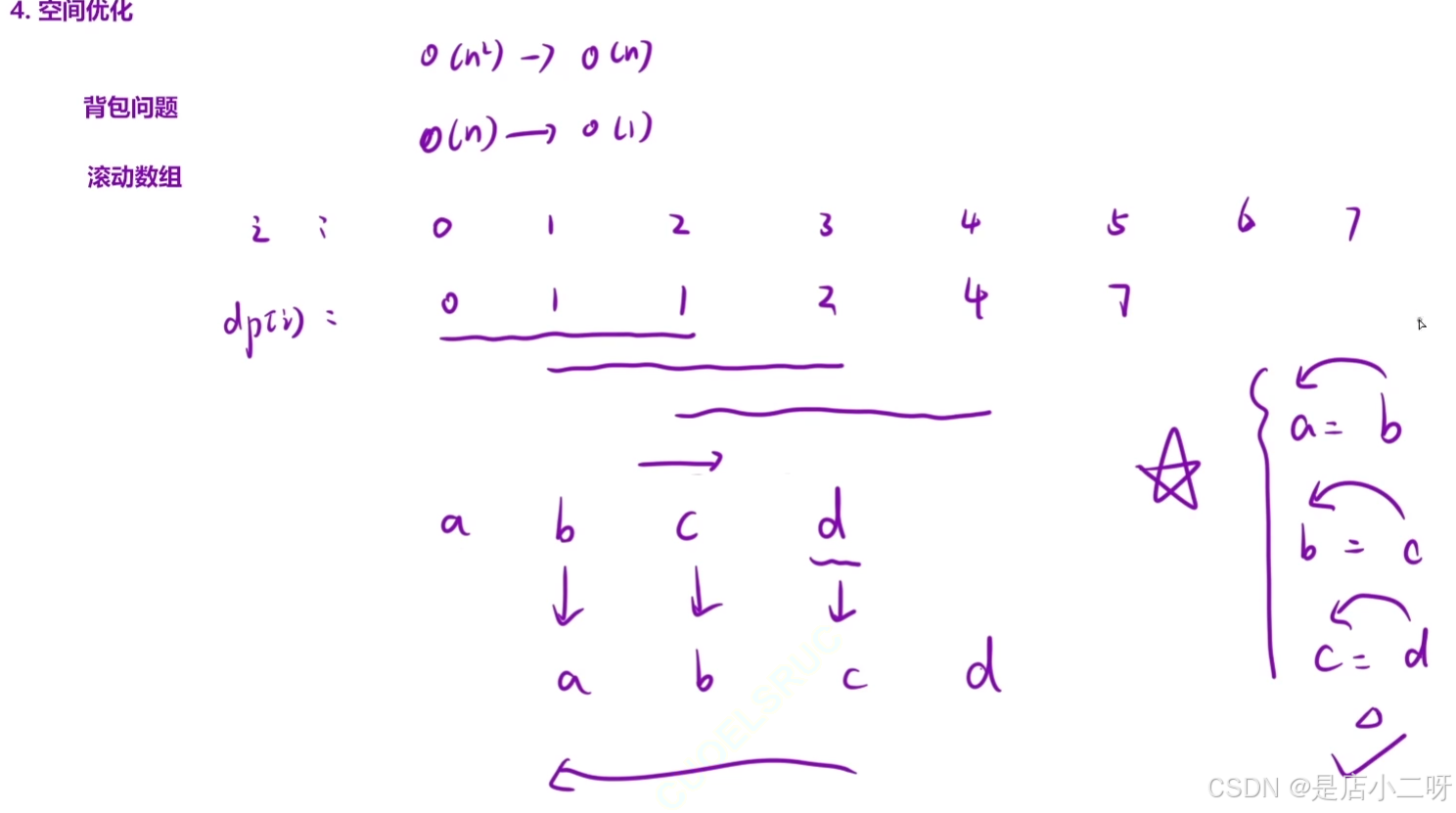
class Solution {
public:int tribonacci(int n) {if(n == 0) return 0;if(n == 1 || n == 2) return 1;vector<int> dp(n + 1);int a = 0, b = 1, c = 1, d = 0;for(int i = 3; i <= n; i++){d = a + b + c;//滚动操作 a = b; b = c; c =d;}return d;}
};

---

面试题 08.01. 三步问题

【题目】：面试题 08.01. 三步问题

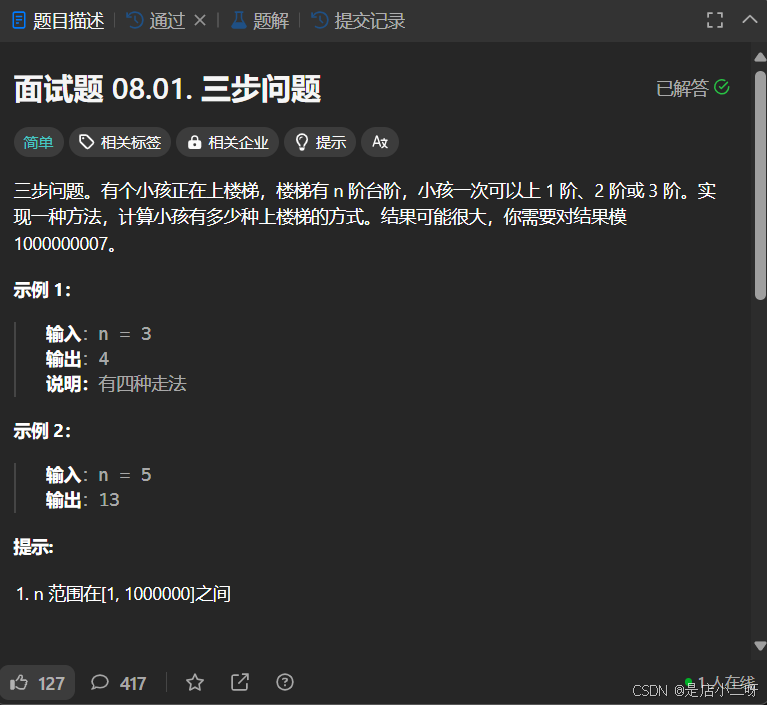
【算法思路】

面对未知的题目时，可以通过绘图寻找线索，帮助解决问题。例如，在这道题中，确定一个位置并列举所有可能情况，可以发现规律。比如，表示i位置前面三次的情况，所有可能组合加起来就是i位置的答案。

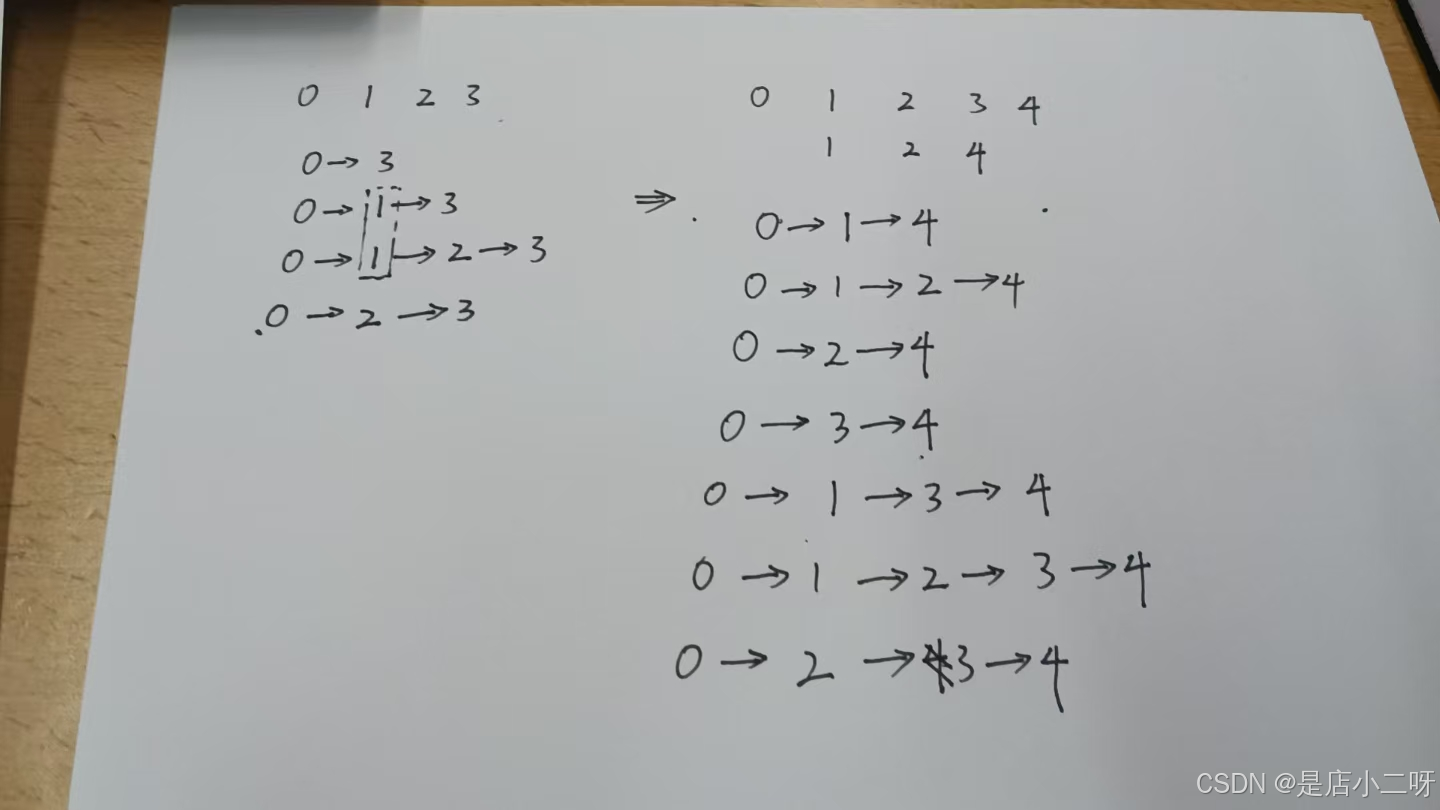
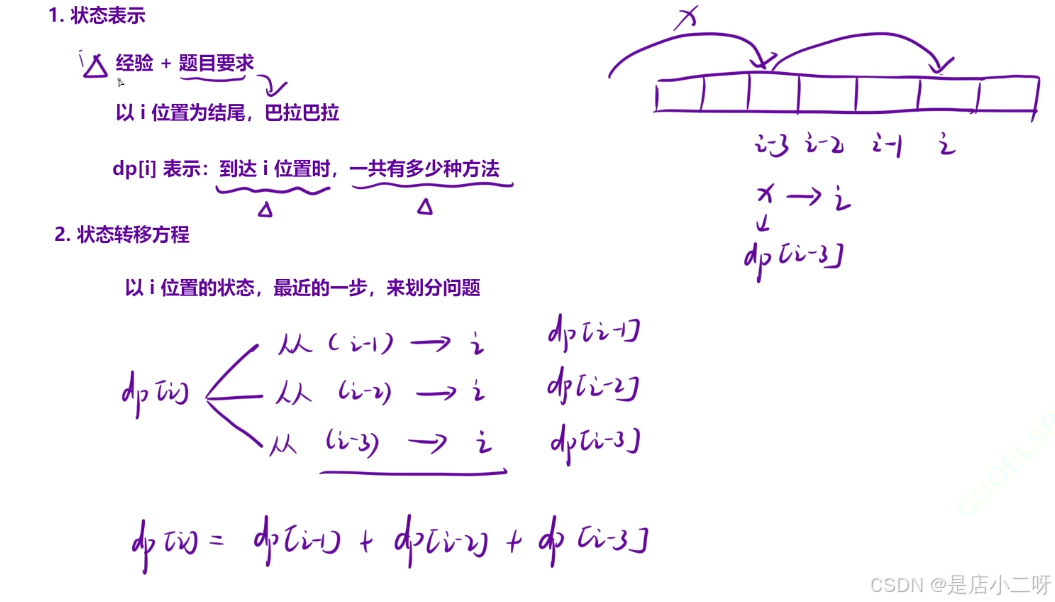
笔试中不需要使用滚动数组，也不用花时间去做空间优化。平时不必刻意练习这些，效果有限。

【代码实现】

class Solution {
public:int waysToStep(int n) {//1.创建dp表vector<int> dp(n + 2);if(n == 1 || n == 2) return n;if(n == 3) return 4;const int MOD = 1e9 + 7;//2.初始化dp[1] = 1;dp[2] = 2; dp[3] = 4;//3.填表for(int i = 4; i <= n; i++)dp[i] = ((dp[i - 1] + dp[i - 2])%MOD + dp[i - 3])%MOD;return dp[n];}
};

【细节问题】

对于这类需要取模的问题，每次计算（如加法、乘法等）都要取一次模，以防止溢出，否则答案可能会错误

---

LCR 088. 使用最小花费爬楼梯

【题目】：LCR 088. 使用最小花费爬楼梯

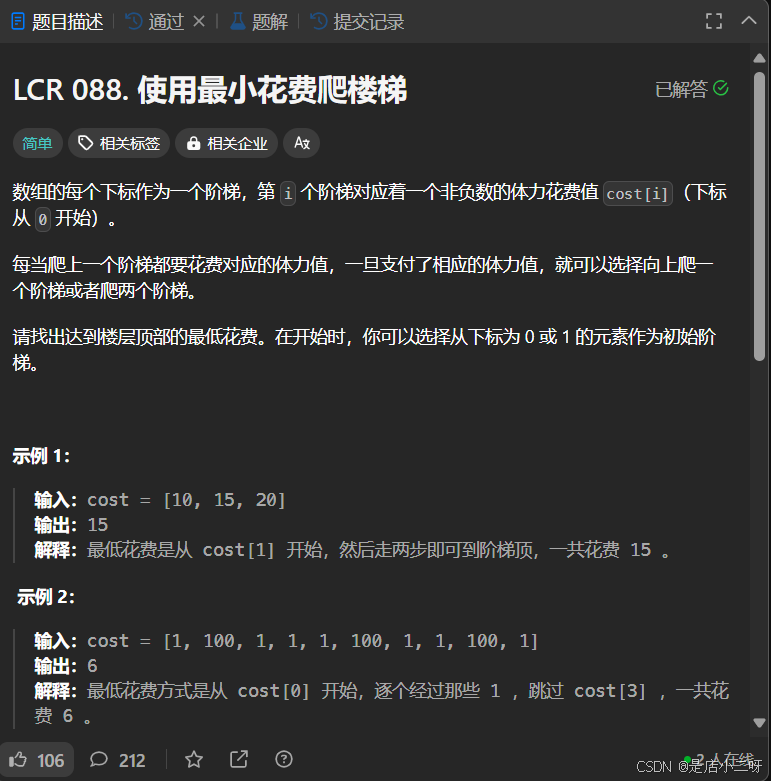
【算法思路】

解法一：

【小技巧】：通过之前或之后的状态推导出 dp[i] 的值。这类问题通常需要通过隐含或明确的递推关系来确定某个位置的数值。

【代码实现】

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n = cost.size();//1.创建dp表vector<int>dp (n + 1);//2.初始化dp[0] = dp[1] = 0;//3.填表for(int i = 2; i <= n; i++)dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);return dp[n];}
};

【算法思路】

解法二：

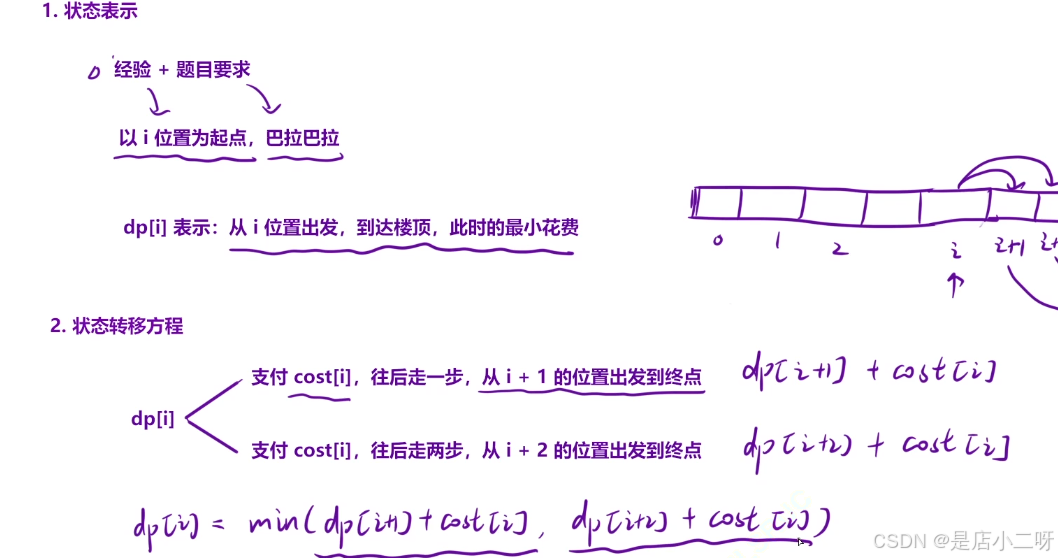
【代码实现】

class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n = cost.size();//1.创建dp表vector<int>dp (n);//2.初始化dp[n - 1] = cost[n -1]; dp[n - 2] = cost[n - 2];//3.填表for(int i = n - 3; i >= 0; i--)dp[i] = min(dp[i + 1], dp[i + 2]) + cost[i];return min(dp[0], dp[1]);}
};

---

91. 解码方法

【题目】：91. 解码方法

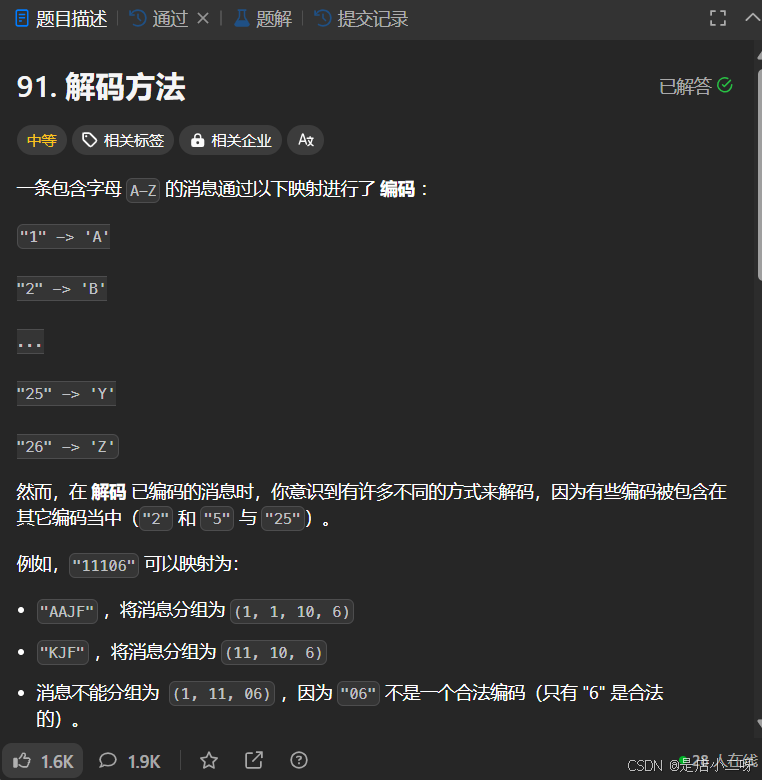
【算法思路】

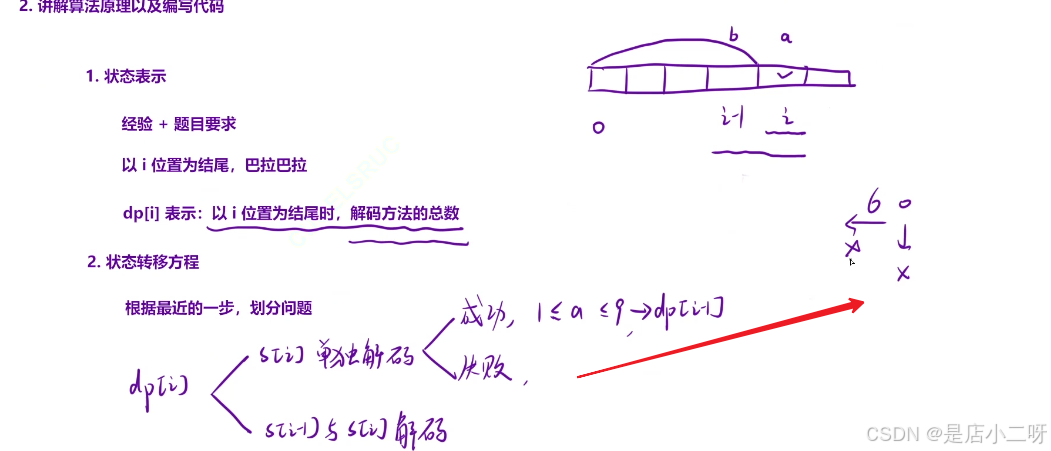
我们使用 dp[i] 表示以位置 i 结尾时的解码方法总数。在分析位置 i 时，需要考虑两种情况：一种是单独解码 s[i]，另一种是将 s[i-1] 和 s[i] 结合解码。对于后者，必须满足 s[i-1]s[i] 形成一个有效的两位数（即在1到26之间，且没有前导零）。

因此，状态转移方程为：dp[i] = dp[i-1] + dp[i-2]，但只有在满足解码条件时，才能进行累加。这样，我们能够从整体上分析解码的方案，而不是孤立地考虑每个子问题的解。

【个人思考】

通过整体思路来解决解码方案问题，结合这两张图片，可以更直观地理解解法。

为什么是相加，难道不会重复吗？其实，每个位置的解码方式是基于前面所有元素的解码结果，解法数量是通过添加‘单独解码’和‘双位解码’的方式得到的。因此，需要将之前的解码方案数相加，因为每个步骤都是缺一不可的。

【代码实现】

class Solution {
public:int numDecodings(string s) {              int n = s.size();//1.创建dp表vector<int> dp(n);//2.初始化dp[0] = s[0] != '0';if(n == 1) return dp[0];if(s[1] >= '1' && s[1] <= '9') dp[1] += dp[0];int t = (s[0] - '0') * 10 + (s[1] - '0');if(t >= 10 && t <= 26) dp[1] += 1;//3.填表操作for(int i = 2; i < n; i++){if(s[i] >= '1' && s[i] <= '9') dp[i] += dp[i - 1];int t = (s[i - 1] - '0') * 10 + (s[i] - '0');if(t >= 10 && t <= 26) dp[i] += dp[i - 2];}return dp[n - 1];}
};

快和小二一起踏上精彩的算法之旅！关注我，我们将一起破解算法奥秘，探索更多实用且有趣的知识，开启属于你的编程冒险！