二叉树（Binary Tree）是一种每个节点最多有两个子节点的树形数据结构，这两个子节点分别称为左子节点和右子节点。二叉树是计算机科学中最基础、最常用的树结构之一，广泛应用于搜索、排序、表达式解析等领域！

核心特点

1. 节点结构
   每个节点包含三部分：

   • 数据域（存储值）

   • 左指针（指向左子节点）

   • 右指针（指向右子节点）

2. 递归定义
   二叉树可以是：

   • 空树（无节点），或

   • 根节点 + 左子树（二叉树） + 右子树（二叉树）。

3. 子树有序性
   左右子树的顺序不能颠倒（即使只有一个子节点，也需明确是左还是右）。

 

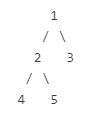
• 节点1是根，2和3是1的左右子节点。

• 节点2的左子节点是4，右子节点是5。

• 节点4和5是叶子节点（无子节点）。

到这应该了解了什么是二叉树了，然后再介绍几个基础二叉树的类型。

1.满二叉树

可以这么理解：一棵二叉树是满二叉树，当且仅当每个节点要么是叶子节点，要么恰好有两个子节点。

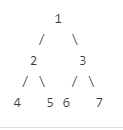
若满二叉树的高度为h，则节点总数为2^h-1；

2.完全二叉树

定义：

一棵二叉树是完全二叉树，当且仅当：

• 除最后一层外，所有层都被完全填满（即达到最大节点数），且

• 最后一层的所有节点都连续集中在左侧（中间不能有空缺）这个很重要！

        √

        ×

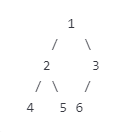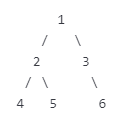3.二叉搜索树

又称二叉查找树或二叉排序树，是一种节点值有序排列的特殊二叉树，支持高效的动态查找、插入和删除操作。

二叉搜索树满足以下递归性质：

1. 左子树中所有节点的值小于当前节点的值；

2. 右子树中所有节点的值**大于（或等于）**当前节点的值；

3. 每个节点的左、右子树本身也是二叉搜索树；

4. 一般不允许重复值（可根据具体实现决定）。

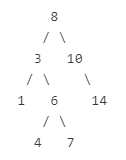
假设要查找7：

• 从根 8 开始，7 < 8 → 走左子树；

• 到节点 3，7 > 3 → 走右子树；

• 到节点 6，7 > 6 → 走右子树；

• 找到 7，查找成功。

应用场景

• 动态集合的查找（如C++ STL的set、map）

• 数据库索引（B+树是BST的扩展）

• 表达式求值与符号表管理

二叉搜索树 = 二分查找思想 + 二叉树结构，既支持高效查找，又能动态维护数据，但必须注意保持平衡以避免性能退化。

4.平衡二叉搜索树（红黑树）

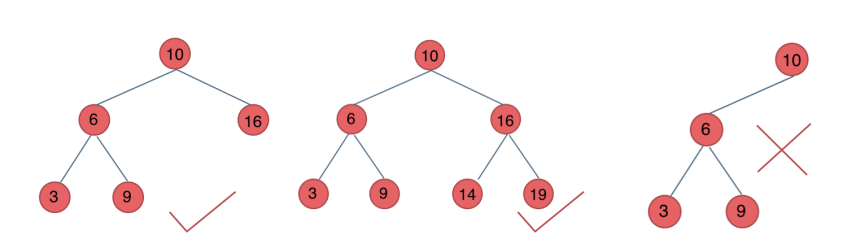
这个和二叉搜索树就多了一个“平衡”，它首先满足二叉搜索树的所有性质。

平衡体现在哪里呢？任意节点的左右子树高度差 ≤ 1

实际应用：

• 数据库索引：AVL树和红黑树用于实现内存索引

• 动态排序：AVL树可实时维护有序数据；

• 优先队列：红黑树实现高效插入/删除的优先队列

平衡二叉搜索树 = 二叉搜索树 + 自动平衡机制，通过牺牲少量维护成本，换取稳定的 O(log n) 性能，是高性能存储与检索的核心数据结构

就简单记一下，更详细的版本去看代码随想录