嘿，各位技术潮人！好久不见甚是想念。生活就像一场奇妙冒险，而编程就是那把超酷的万能钥匙。此刻，阳光洒在键盘上，灵感在指尖跳跃，让我们抛开一切束缚，给平淡日子加点料，注入满满的passion。准备好和我一起冲进代码的奇幻宇宙了吗？Let's go！

我的博客：yuanManGan

我的专栏：C++入门小馆 C言雅韵集 数据结构漫游记  闲言碎语小记坊 题山采玉 领略算法真谛

红黑树的介绍

红黑树也是一棵平衡二叉树，我们之前实现的AVL树，他是通过多次的旋转而得到的平衡，付出了相应的代价，让平衡因子的绝对值小于2，才使我们二叉树的高度实现了log n,而我们的红黑树要求最长路径不超过最短路径的两倍，通过一下条件来实现：

1.每个节点不是红色就是黑色，

2.根节点是黑色的

3.每条路径的黑色节点数相同

4.不存在连续的红色节点

我们就通过这些条件来实现最长路径不超过最短路径的两倍

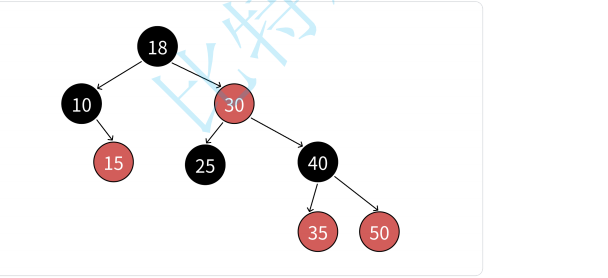
注意我们的完整的一条路径是到左右子树为空的路径

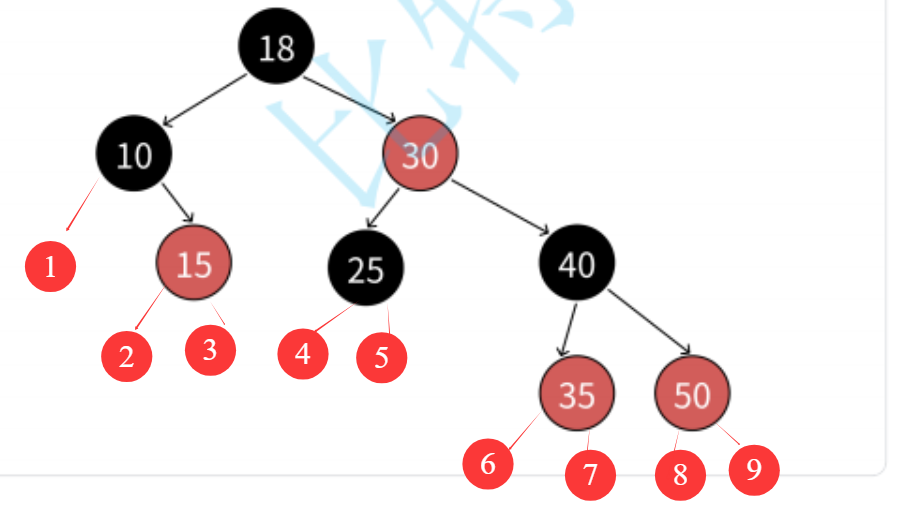
像这样的一棵树他的路径数就是9条。

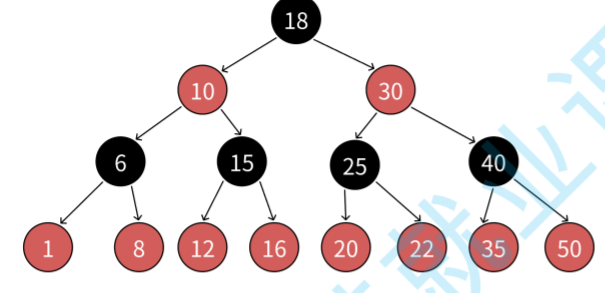
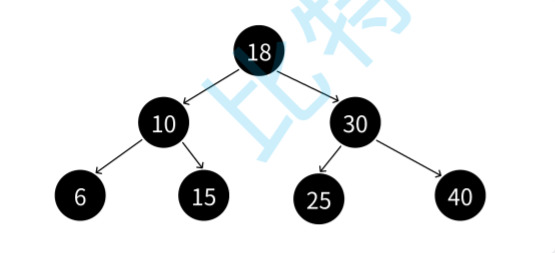
红⿊树如何确保最⻓路径不超过最短路径的2倍的？

由规则3可知，从根到NULL结点的每条路径都有相同数量的⿊⾊结点所以极端场景下，最短路径 就就是全是⿊⾊结点的路径，假设最短路径⻓度为bh(black height)

由规则2和4可知，任意⼀条路径不会有连续的红⾊结点，所以极端场景下，最⻓的路径就是⼀ ⿊⼀红间隔组成，那么最⻓路径的⻓度为2*bh。

综合红⿊树的4点规则⽽⾔，理论上的全⿊最短路径和⼀⿊⼀红的最⻓路径并不是在每棵红⿊树都 存在的。假设任意⼀条从根到NULL结点路径的⻓度为x，那么bh <= h <= 2*bh。

红⿊树的效率：

假设N是红⿊树树中结点数量，h最短路径的⻓度，那么 , 由此推出 ，也就是意味着红⿊树增删查改最坏也就是⾛最⻓路径 ，那么时间复杂度还是 。 2^ h − 1 <= N < 2 ^(2∗h) − 1

h ≈ logN 也就是意味着红⿊树增删查改最坏也就是⾛最⻓路径2 ∗ logN ，那么时间复杂度还是 O(logN)。

红⿊树的结构

#pragma once
enum Colour
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{pair<K, V> _kv;RBTreeNode<K, V>* _parent;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _left;Colour _col;RBTreeNode(const pair<K, V>& kv): _kv(kv), _right(nullptr), _left(nullptr), _col(BLACK){}
};
template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;public:
private:Node* _root = nullptr;
};

红⿊树的插⼊

我们的插入过程的前半部分和二叉搜索树的过程基本一样，先找到插入的位置插入后，进行平衡调整。

bool Insert(const pair<K, V>& kv)
{if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv)cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;
}

我们再来想想如果我们要插入一个节点，我们该插入红色节点还是黑色节点呢？我们要保证每个路径的黑色节点数相同，如果我们插入黑色节点的话我们就得让别的路径的黑色节点都加一才行，所以我们最好插入红色节点，如果我们插入的节点的位置的父节点是黑色的就万事大吉，不用进行操作了。

那遇到了父亲为红色节点时我们就得进行变色操作了，

情况1：

p为红，那么因为p为红那么g就不可能为红，这里只有u是未知的，假如u为红时，我们就得将p和u都变成黑色，然后让g变成红，然后继续向上更新答案，直到更新为parent节点为空或者为黑的时候就结束。

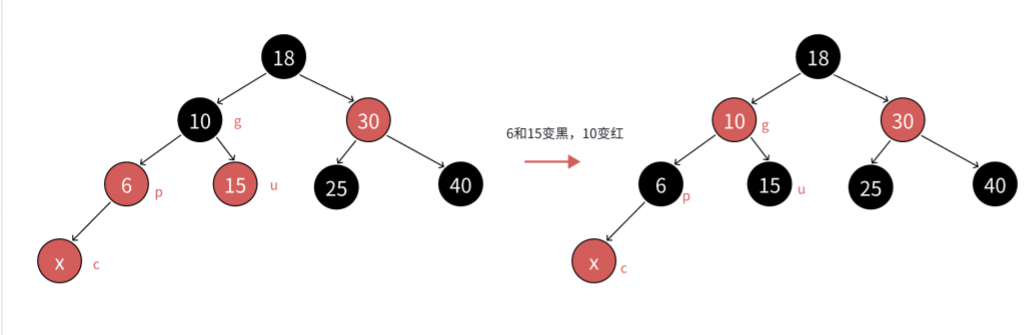
这是我们这种情况的抽象图：

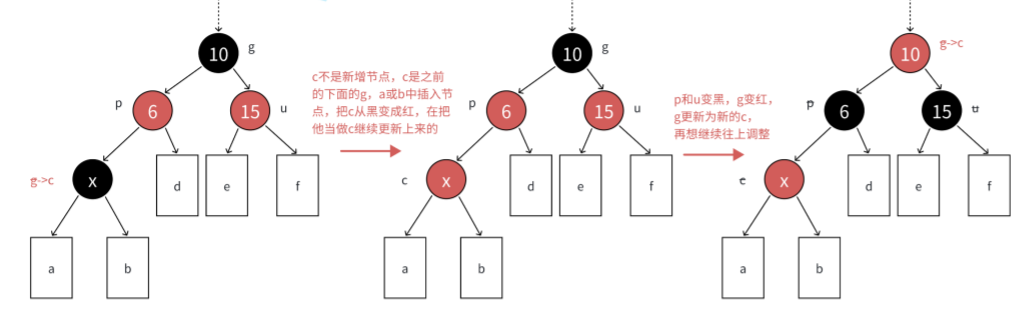
 情况二：单旋+变⾊

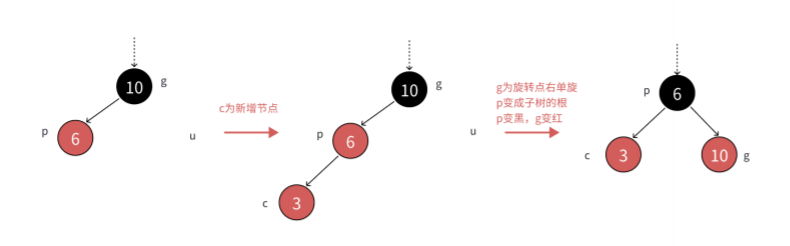
当我们往一个红色节点的左边插入节点时，此时g的右节点为空或者时黑色，我们不能像刚刚那样操作了，如果我们像那样操作，我们没有u节点，然后操作后g的右支路的黑色节点数会多一个我们就需要将g节点进行右旋操作，让p节点成为c和g节点的根节点。

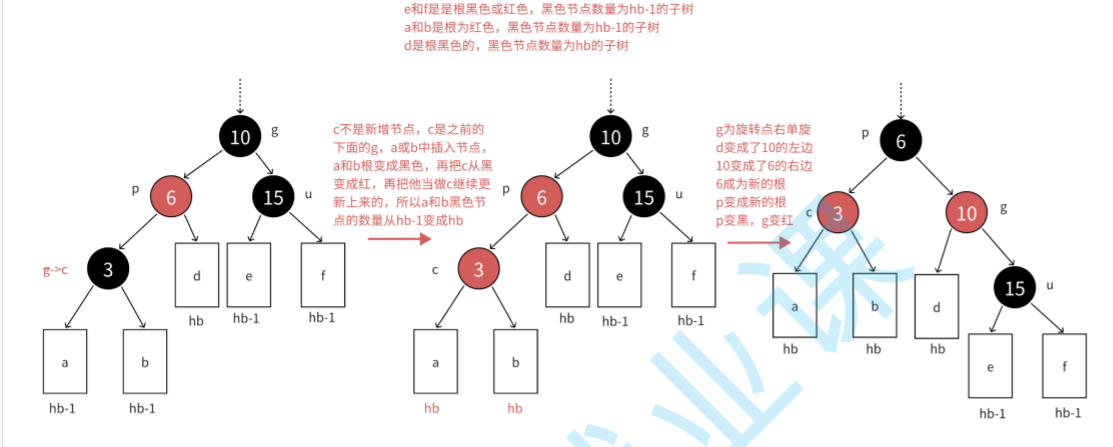
情况三：双旋加变色：

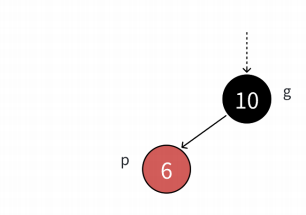
我们往这个树的p位置的右孩子插入一个节点时就变成了

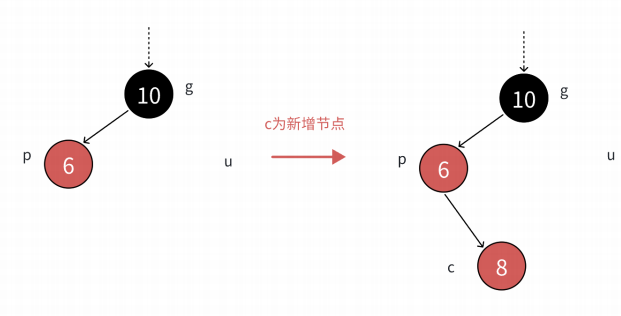
我们得先对p节点进行右旋操作就成了：

 

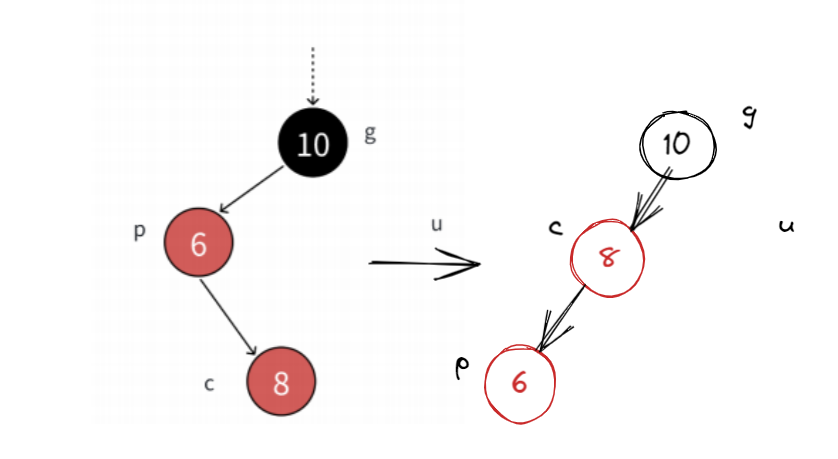
这个样子就比较熟悉了，我们再右旋g变个色就解决了。

 

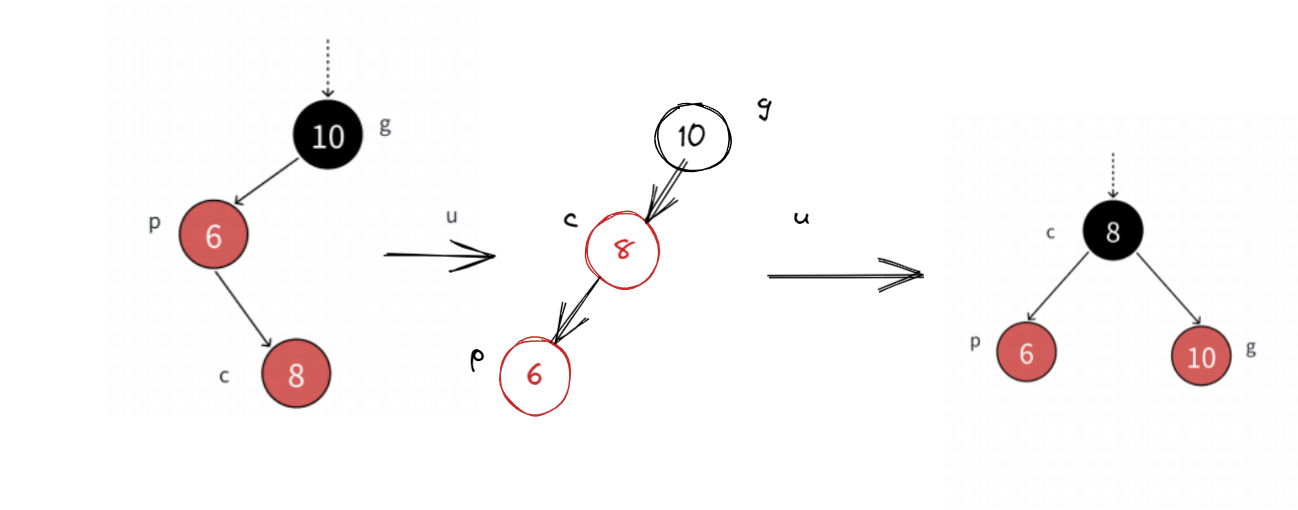
同样的思路，当u存在且为黑时也是一样的解决方法。

插入完整的代码如下：

	bool Insert(const pair<K, V>& kv){if (_root == nullptr)  // 新增：处理根节点为空{_root = new Node(kv);_root->_col = BLACK;return true;}Node* cur = _root;Node* parent = nullptr;//插入操作while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{//插入失败return false;}}//新插入红色节点cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first){parent->_right = cur;}elseparent->_left = cur;cur->_parent = parent;while (parent && parent->_col == RED){Node* grandfather = parent->_parent;if (parent == grandfather->_left){Node* uncle = grandfather->_right;//1.u存在且为红if (uncle && uncle->_col == RED){//变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续往上处理cur = grandfather;parent = cur->_parent;}else{//     g//   p   u// cif (cur == parent->_left){RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//     g//   p   u//     cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else // (parent == grandfather->_right){Node* uncle = grandfather->_left;//1.u存在且为红if (uncle && uncle->_col == RED){//变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续往上处理cur = grandfather;parent = cur->_parent;}else{//     g//   u   p//          cif (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{//     g//   u   p//     cRotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;return true;}