一、单项选择题(每小题3分,共15分)
1. 用3个“1”和4个“0”能组成( )个不同的二进制数字。
A. 35 B. 36, C. 37, D. 38
2. 整除300的正整数的个数为( )。
A. 14 B. 16 C. 18 D. 20
3. 由6个人围坐一周,有( )种坐法。
A. 3!, B. 4!, C. 5!, D. 6!
4. 在1到350中,能被11整除的整数的个数为( )。
A.30, B. 31, C.32, D. 33
5. 边长为1的正三角形中,放入( )个点,就一定能保证至少有两个点之间的距离小于等于1/3。
A. 4, B. 6, C.8, D. 10
二、解答题(第1小题5分,其他每小题10分,共85分)
1. 在格路模型中,求从点(0,0)出发,经过点(3,7),到达点(10,10)的格路条数? (5分)
解:格路条数为:

2. 求不含数字3和数字8,各位数字相异且大于5400的四位数的个数.(10分)
解:设所求的满足题意的四位数共有N个,它们可分成如下两类:
(1)千位数字为5的四位数 因为百位数字可以是4,6,7,9类的四位数有
4·P(6,2)=120个.
(2)千位数字大于5的四位数.因为干位数字可以是6,7,9这3个数之一,故属于此类的四位数有
3·P(7,3)=630个
由加法原则得
N=120十630=750.
3. 从1,2,…,30中选取3个相异的正整数,使得它们的和能被3整除,有多少种选取方法? (10分)
解:设所求为N.以Ai(i=0、l、2)表示由集合{1,2,….30}中的除以3所得余数为i的整数所成之集,则|A0|=|A1|=|A2|=10.满足题意的N种选取方法可分成如下两类:
(1)使得所选3个整数都属于同一个Ai(i=0,1,2)的选取方法, 属于此类的选取方法共有
3C(10,3)=360种.
(2)使得所选3个整数分别属于A0,Al,A2的选取方法, 属于此类的选取方法共有
10 ×10×10=1000种.
由加法原则得
N=360十l000=1360.
4.求由n(n≥2)个相异元1,2,…,n作成的1不排在第一位,2不排在第二位的全排列的个数。(10分)
解:设所求为N.因为由n(n≥2)个相异元1,2,…n作成的1不排在第一位的全排列共有(n—1) (n—1)!,其中2排在第二位的全排列有(n—2)·(n—2)!个,故
N=(n一1)·(n—1)!一(n一2)·(n一2)!
=(n2一3n十3)·(n一2)!.
5. 求从1至500的整数中能被7或11整除的整数的个数。(10分)
解:设所求为N.令S={1,2,…,500},A、B分别表示S中能被7、能被11整除的整数所成之集,则

6. 求解递推关系:(10分)
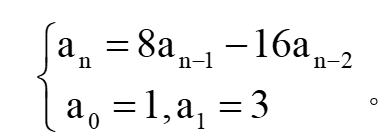
解:特征方程:
![]()
特征根:
![]()
递推关系的通解:
![]()
,其中C1、C2是任意常数。
将初始条件代入得:

故递推关系的解为:
![]()
7. 利用母函数求解:若有1克砝码3枚、2克砝码4枚、4克砝码2枚的砝码各一枚,问能称出那几种重量?各有几种方案?(10分)
解:所求问题对应的母函数为
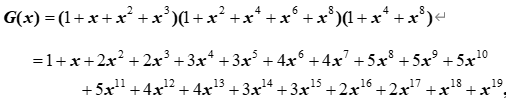
因此,能称出的重量为0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19(克),共20种;其中称出重量为0,1,18,19(克)的方法数各为1种,称出重量为2,3,16,17(克)的方法数各为2种,称出重量为4,5,14,15(克)的方法数各为3种,称出重量为6,7,12,13(克)的方法数各为4种,称出重量为8,9,10,11(克)的方法数各为5种。
8.将一长木条等分成7块区域,如图所示,请利用波利亚计数定理,求:用3种颜色给每个区域着色,不同的着色方案有多少种?(10分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
解:木条刚体运动的所有可能的置换:
g0=(1)(2)(3)(4)(5)(6)(7)
g1=(17)(26)(35)(4)
则根据波利亚计数定理,不同的着色方案数为:

9.在一手镯上均匀嵌上5颗带色的珠子,请用指数型波利亚计数定理计算恰好嵌入的是3个蓝色、2个红色珠子的不同方案数?(10分)
解:设5颗珠子依次编号为1、2、3、4、5,则手镯刚体运动所得的置换有:
g0=(1)(2)(3)(4)(5), g1=(1)(25)(34),
g2=(2)(13)(45), g3=(3)(24)(15),
g4=(4)(12)(35), g5=(5)(14)(23)
g6=(12345), g7=(13524),
g8=(14253), g9=(15432)。
那么,对应的循环指数多项式为:
![]()
其中,x3y2的系数为
![]()
也即嵌入的是3个蓝色、2个红色珠子的不同方案数是2。
(参考答案)
一、单项选择题(每小题3分,共15分)
1.A 2.C 3.C 4.B 5.D
二、解答题(第1小题5分,其他每小题10分,共85分)
1. 在格路模型中,求从点(0,0)出发,经过点(3,7),到达点(10,10)的格路条数? (5分)
解:格路条数为:

2. 求不含数字3和数字8,各位数字相异且大于5400的四位数的个数.(10分)
解:设所求的满足题意的四位数共有N个,它们可分成如下两类:
(1)千位数字为5的四位数 因为百位数字可以是4,6,7,9类的四位数有
4·P(6,2)=120个.
(2)千位数字大于5的四位数.因为干位数字可以是6,7,9这3个数之一,故属于此类的四位数有
3·P(7,3)=630个
由加法原则得
N=120十630=750.
3. 从1,2,…,30中选取3个相异的正整数,使得它们的和能被3整除,有多少种选取方法? (10分)
解:设所求为N.以Ai(i=0、l、2)表示由集合{1,2,….30}中的除以3所得余数为i的整数所成之集,则|A0|=|A1|=|A2|=10.满足题意的N种选取方法可分成如下两类:
(1)使得所选3个整数都属于同一个Ai(i=0,1,2)的选取方法, 属于此类的选取方法共有
3C(10,3)=360种.
(2)使得所选3个整数分别属于A0,Al,A2的选取方法, 属于此类的选取方法共有
10 ×10×10=1000种.
由加法原则得
N=360十l000=1360.
4.求由n(n≥2)个相异元1,2,…,n作成的1不排在第一位,2不排在第二位的全排列的个数。(10分)
解:设所求为N.因为由n(n≥2)个相异元1,2,…n作成的1不排在第一位的全排列共有(n—1) (n—1)!,其中2排在第二位的全排列有(n—2)·(n—2)!个,故
N=(n一1)·(n—1)!一(n一2)·(n一2)!
=(n2一3n十3)·(n一2)!.
5. 求从1至500的整数中能被7或11整除的整数的个数。(10分)
解:设所求为N.令S={1,2,…,500},A、B分别表示S中能被7、能被11整除的整数所成之集,则

6. 求解递推关系:(10分)
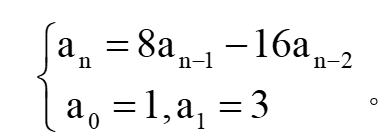
解:特征方程:
![]()
特征根:
![]()
递推关系的通解:
![]()
,其中C1、C2是任意常数。
将初始条件代入得:

故递推关系的解为:
![]()
7. 利用母函数求解:若有1克砝码3枚、2克砝码4枚、4克砝码2枚的砝码各一枚,问能称出那几种重量?各有几种方案?(10分)
解:所求问题对应的母函数为
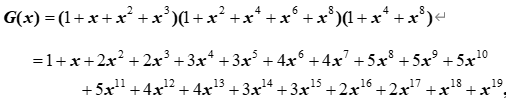
因此,能称出的重量为0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19(克),共20种;其中称出重量为0,1,18,19(克)的方法数各为1种,称出重量为2,3,16,17(克)的方法数各为2种,称出重量为4,5,14,15(克)的方法数各为3种,称出重量为6,7,12,13(克)的方法数各为4种,称出重量为8,9,10,11(克)的方法数各为5种。
8.将一长木条等分成7块区域,如图所示,请利用波利亚计数定理,求:用3种颜色给每个区域着色,不同的着色方案有多少种?(10分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
解:木条刚体运动的所有可能的置换:
g0=(1)(2)(3)(4)(5)(6)(7)
g1=(17)(26)(35)(4)
则根据波利亚计数定理,不同的着色方案数为:

9.在一手镯上均匀嵌上5颗带色的珠子,请用指数型波利亚计数定理计算恰好嵌入的是3个蓝色、2个红色珠子的不同方案数?(10分)
解:设5颗珠子依次编号为1、2、3、4、5,则手镯刚体运动所得的置换有:
g0=(1)(2)(3)(4)(5), g1=(1)(25)(34),
g2=(2)(13)(45), g3=(3)(24)(15),
g4=(4)(12)(35), g5=(5)(14)(23)
g6=(12345), g7=(13524),
g8=(14253), g9=(15432)。
那么,对应的循环指数多项式为:
![]()
其中,x3y2的系数为
![]()
也即嵌入的是3个蓝色、2个红色珠子的不同方案数是2。
)

学习笔记(二)----课程实验环境搭建(wsl2+ubuntu+quem+xv6))
)











之扩展小部件(二十七):如何使用number_input部件?)
)


