零、题目描述
一、为什么这道题值得一看？
二、题目拆解：提取核心要素与约束
三、算法实现：基于 DFS 的面积计算
- 代码拆解
- 时间复杂度
- 空间复杂度
四、与「岛屿数量」的代码对比（一目了然看差异）
五、坑点总结
六、举一反三
七、总结

零、题目描述

题目链接：岛屿的最大面积

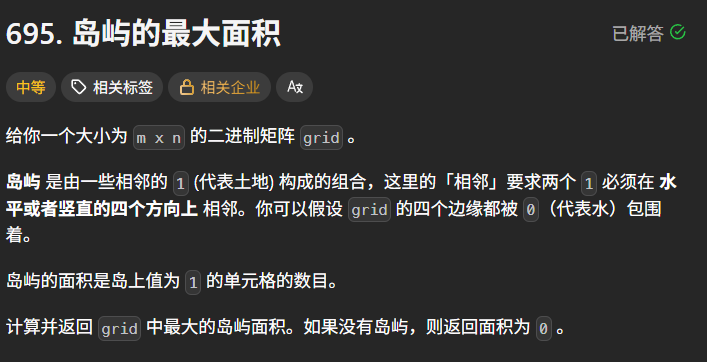
在这里插入图片描述

示例 1：

输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11 ，因为岛屿只能包含水平或垂直这四个方向上的 1 。

示例 2：
输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0

一、为什么这道题值得一看？

如果你是第一次阅读我的题解文章，可能会好奇‘岛屿数量’与这道题的关联 —— 其实，「岛屿的最大面积」是「岛屿数量（LeetCode 200）」的经典进阶题，两者共享几乎相同的搜索框架，只是在目标上从‘统计岛屿个数’变成了‘计算最大面积’。

如果你想更系统地理解「洪水灌溉算法」的基础逻辑（比如 DFS 如何标记连通区域、如何处理边界条件），建议先看看昨天的文章（因为算法原理类似这篇文章讲解算法原理没有上一篇细致嘿嘿）力扣 200.岛屿数量。那里详细拆解了‘如何从 0 到 1 设计岛屿计数的代码’，读懂它再看今天的内容，会对‘搜索算法的复用与调整’有更清晰的认知～

如果你昨天跟着学了「岛屿数量」（LeetCode 200），那么这道题会是绝佳的“进阶练习”——它和前者共享 90% 的核心逻辑，但在细节上的差异能帮你更深刻理解「搜索算法的灵活性」。

从本质上看，两道题都是「连通区域问题」的变种：

前者是计数问题（统计连通区域的数量）；
后者是计量问题（统计单个连通区域的最大规模）。

学会这道题，你能掌握：

如何在搜索过程中累加数据（面积计算的核心）；
如何在多个结果中跟踪最大值；
进一步巩固「洪水灌溉（Flood Fill）」算法的通用框架。

二、题目拆解：提取核心要素与约束

先看原题：

给你一个由 1（陆地）和 0（水）组成的二进制矩阵 grid，请你计算网格中岛屿的最大面积。岛屿是由一些相邻的 1 构成的组合，这里的「相邻」要求两个 1 必须在水平或者竖直的四个方向上相邻。你可以假设 grid 的四个边缘都被 0 包围着。岛屿的面积是岛上值为 1 的单元格的数目。

再结合所给的代码框架和提示：

class Solution {
public:int maxAreaOfIsland(vector<vector<int>>& grid) {}
};

核心要素提炼:

题中给出的是由 vector 组成的二维数组 grid，元素类型是 int，取值只有 0（水）和 1（陆地）；
二维数组的长宽范围是 1 ≤ m, n ≤ 50（m 为行数，n 为列数）；
核心任务是：找到所有由相邻 1 组成的岛屿，计算每个岛屿的面积（1 的数量），并返回其中的最大值；若没有岛屿，返回 0。

关键点:

遍历网格：需用双重循环遍历每个单元格 (i,j)，检查是否为未访问的陆地（grid[i][j] == 1）。
连通性判断：只有水平（左右）或垂直（上下）相邻的 1 属于同一岛屿，斜对角不算，因此搜索时仅需遍历四个方向。
DFS/BFS 搜索：发现陆地时，需通过深度优先或广度优先遍历，找到该岛屿所有相连的 1，并计算面积。
标记已访问：为避免重复计算，需将已统计过的 1 标记为 0（原地修改，无需额外空间）。
面积计算与最大值跟踪：
- 对每个岛屿，通过递归或迭代累加 1 的数量（面积）；
- 用一个变量记录所有岛屿面积中的最大值，遍历完所有岛屿后返回该值。
边界处理：搜索相邻单元格时，需检查坐标是否在网格范围内（0 ≤ x < 行数 且 0 ≤ y < 列数），防止越界。

与「岛屿数量」的共性（可直接复用的逻辑）：

遍历网格：逐个检查每个单元格，发现未访问的陆地（1）时触发搜索；
DFS 搜索：通过递归遍历当前陆地的上下左右，“淹没”（标记为 0）已访问的陆地，避免重复计算；
方向数组：用 dx 和 dy 定义四个方向，简化代码（和昨天的 dx = [1,-1,0,0], dy = [0,0,1,-1] 完全相同）。

关键差异（今天要重点掌握的新逻辑）：

从“计数”到“累加面积”：
- 昨天每触发一次 DFS，就给岛屿数量 +1；
- 今天每触发一次 DFS，需要统计这个岛屿包含多少个 1（即面积），用变量 n 实时累加。
跟踪最大面积：
- 每次 DFS 结束后（一个岛屿被完全“淹没”），将当前岛屿的面积 n 与全局最大面积 max_size 比较，更新最大值。

三、算法实现：基于 DFS 的面积计算

代码拆解

直接结合代码拆解核心逻辑（代码结构和昨天高度相似，重点看注释中标注的差异点）：

class Solution {
public:int rows, cols;int max_size = 0;  // 记录全局最大面积（差异点1）int n = 0;         // 记录当前岛屿的面积（差异点2）int dx[4] = {1, -1, 0, 0};  // 方向数组（复用）int dy[4] = {0, 0, 1, -1};int maxAreaOfIsland(vector<vector<int>>& grid) {rows = grid.size();cols = grid[0].size();for (int i = 0; i < rows; i++) {for (int j = 0; j < cols; j++) {if (grid[i][j] == 1) {  // 发现新岛屿n = 0;              // 重置当前岛屿面积（差异点3）dfs(i, j, grid);    // 遍历整个岛屿，计算面积max_size = max(max_size, n);  // 更新最大面积（差异点4）}}}return max_size;}void dfs(int x, int y, vector<vector<int>>& grid) {grid[x][y] = 0;  // 淹没当前陆地（标记已访问，复用）n++;             // 当前岛屿面积+1（差异点5）// 遍历四个方向（复用）for (int i = 0; i < 4; i++) {int nx = x + dx[i];int ny = y + dy[i];// 检查边界+是否为未访问的陆地（复用）if (nx >= 0 && ny >= 0 && nx < rows && ny < cols && grid[nx][ny] == 1) {dfs(nx, ny, grid);  // 递归计算相邻陆地}}}
};

核心差异点深度解析:
上面的代码中，标为“差异点”的部分是今天的核心，我们逐个拆解：

变量 n 和 max_size 的作用：
- n：临时记录当前正在遍历的岛屿的面积，每次发现新岛屿时重置为 0；
- max_size：全局变量，始终存储所有岛屿中最大的面积，每次一个岛屿遍历结束后更新。
举例：如果网格中有 3 个岛屿，面积分别是 3、6、2，那么 max_size 会在遍历完第一个岛屿后变为 3，第二个后变为 6，第三个后保持 6。
n 的累加时机：
进入 dfs 后，先将当前陆地标记为 0（避免重复访问），然后立即执行 n++——因为当前单元格是陆地（1），本身就贡献 1 个面积。

反例：如果在递归结束后才 n++，会漏掉当前单元格的面积，导致结果偏小。
max_size 的更新时机：
当一个岛屿的 DFS 完全结束后（即 dfs(i,j,grid) 执行完毕），n 已经记录了这个岛屿的完整面积，此时用 max(max_size, n) 比较并更新最大值。

分步运行示例（以示例 1 中最大岛屿为例）
为了更直观理解 n 和 max_size 的变化，我们以示例 1 中面积为 6 的岛屿为例，跟踪代码的关键执行步骤：

初始状态：
遍历网格时，首次遇到该岛屿的第一个陆地（坐标 (7,7)，假设网格行索引从0开始），此时 grid[7][7] == 1。
触发DFS前：
- 初始化 n = 0（准备统计当前岛屿面积）；
- 调用 dfs(7,7,grid)。
DFS递归过程：
- 第一层递归（7,7）：
  grid[7][7] 改为 0（标记已访问），n 累加为 1；
  检查四个方向，发现右侧 (7,8) 和上方 (6,7) 是陆地，优先递归 (7,8)。
- 第二层递归（7,8）：
  grid[7][8] 改为 0，n 累加为 2；
  检查方向，发现上方 (6,8) 是陆地，递归 (6,8)。
- 第三层递归（6,8）：
  grid[6][8] 改为 0，n 累加为 3；
  检查方向，发现左侧 (6,7) 是陆地，递归 (6,7)。
- 第四层递归（6,7）：
  grid[6][7] 改为 0，n 累加为 4；
  检查方向，发现左侧 (6,6) 是水，下方 (7,7) 已访问，继续递归其他方向…
- 后续递归：依次访问 (6,9)、(7,9) 等相连陆地，n 逐步累加至 6。
DFS结束后：
该岛屿的所有陆地已被“淹没”（改为 0），n 的值为 6；
此时比较 n 与 max_size（初始为 0），更新 max_size = 6。

通过这个过程可见：n 会随着递归深入实时累加，而 max_size 仅在整个岛屿遍历结束后更新，确保记录的是“完整岛屿”的最大面积。

时间复杂度

操作类型	时间复杂度	说明
网格整体遍历	O(m×n)	需通过双重循环遍历网格的每个单元格（共m×n个），检查是否为未访问的陆地
DFS递归处理	O(m×n)	每个陆地单元格（`1`）最多被访问一次（被标记为`0`后不再处理）
面积计算与比较	O(1)	每个岛屿的面积累加（`n++`）和最大值更新（`max(max_size, n)`）均为常数操作
总计	O(m×n)	m为网格行数，n为列数，整体时间由遍历和递归的总操作数决定

补充说明：

时间复杂度的核心瓶颈是“网格遍历”和“DFS递归”，两者的总操作次数均与网格大小（m×n）成正比，因此整体复杂度为O(m×n)。
由于题目中网格规模较小（m, n ≤ 50），即使是最坏情况（全为陆地），总操作次数也仅为50×50=2500次，DFS递归栈深度不会导致栈溢出，效率完全可控。

空间复杂度

消耗场景	空间复杂度	说明
递归调用栈（DFS）	O(m×n)	最坏情况下（网格全为陆地，如 50×50 的全 `1` 网格），递归深度会达到网格总单元格数（`m×n`），此时栈空间消耗与网格规模成正比。
原地修改（无额外空间）	O(1)	算法通过直接修改原网格（将访问过的 `1` 改为 `0`）标记“已访问”，未使用额外的数据结构（如哈希表、布尔数组），因此仅消耗常数级空间。

补充说明：

空间复杂度的瓶颈在于 DFS 的递归栈深度。由于题目中网格最大为 50×50，即使全为陆地，递归深度也仅为 2500，远低于大多数编程语言的栈空间上限（通常为 10^4~105），因此不会出现栈溢出问题。
若改用 BFS 实现（用队列存储待访问坐标），空间复杂度同样为 O(m×n)（最坏情况下队列会存储所有陆地坐标），但避免了递归栈的限制，适合更大规模的网格场景。

四、与「岛屿数量」的代码对比（一目了然看差异）

为了更清晰地看出两道题的关系，我们用表格对比核心代码：

功能点	岛屿数量（LeetCode 200）	岛屿的最大面积（LeetCode 695）
核心目标	统计岛屿的个数	统计最大岛屿的面积
关键变量	`sum`（岛屿计数器）	`n`（当前岛屿面积）、`max_size`（最大面积）
触发搜索后操作	`sum++`（每找到一个岛屿，计数器+1）	`n=0` → 执行 DFS → `max_size = max(...)`
DFS 内部操作	仅标记陆地为 `0`，无额外计算	标记陆地为 `0` 后，执行 `n++`（累加面积）

五、坑点总结

忘记重置 n：
如果在发现新岛屿时没有将 n 重置为 0，会导致多个岛屿的面积累加在一起（比如前一个岛屿面积 3，后一个会从 3 开始加），结果错误。
max_size 初始化错误：
若初始化为 1 而非 0，当网格中没有岛屿（全为 0）时，会错误返回 1 而非 0。
混淆 n 和 max_size 的作用：
不要在递归过程中更新 max_size，必须等一个岛屿完全遍历结束后再更新——否则可能把不完整的面积当作最大值。

六、举一反三

掌握了“计数”和“算面积”这两种变体，你可以尝试解决更复杂的连通区域问题：

LeetCode 130. 被围绕的区域：判断哪些 ‘O’ 被 ‘X’ 完全包围（从边界的 ‘O’ 出发标记所有连通区域，未标记的 ‘O’ 则被包围，需替换为 ‘X’）。
LeetCode 1020. 飞地的数量：计算无法从边界离开的陆地面积（在 DFS 基础上增加“是否触达边界”的判断）；

这些问题的核心依然是「Flood Fill 搜索框架」，只是在“统计目标”上做了微调——学会透过问题看本质，算法学习会事半功倍。