好久不见~我又回来了

这一节我们来讲一讲图像在计算机中的本质，以及全连接神经网络的缺陷，进而引出卷积神经网络

---

一、图像在计算机中的本质

不知道你有没有学过数据结构，在讲这一部分的时候对数组进行了扩展，讲到了广义表和压缩矩阵，其中压缩矩阵用来压缩图像信息进行传递。

在计算机中，图像本质上是一个数字矩阵。每个像素点对应一个数值，表示颜色或亮度信息。
具体来说：

• 对于灰度图像，它是一个二维矩阵 $I\in {\mathbb{R}}^{H\times W}$，其中 $H$ 是高度（行数），$W$ 是宽度（列数），每个元素 $I(i,j)$ 表示像素在位置 $(i,j)$ 的灰度值（范围通常为 $0$ 到 $255$）。

• 例如下面这两张图

• 

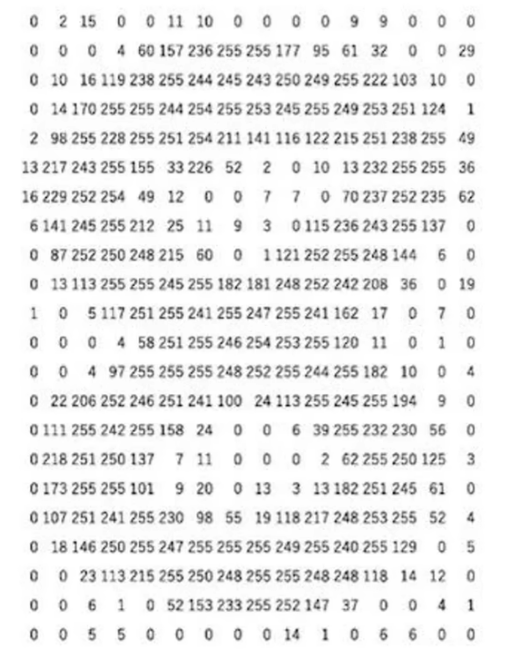
• 对于彩色图像（如 RGB 格式），它是一个三维张量 $I\in {\mathbb{R}}^{H\times W\times C}$，其中 $C$ 是通道数（通常 $C=3$，对应红、绿、蓝三个通道）。每个元素 $I(i,j,k)$ 表示位置 $(i,j)$ 在通道 $k$ 的颜色强度。

例如，一个 $32\times 32$ 的 RGB 图像可表示为：
$$I=\left[\begin{array}{ccc}[I_{11}^R,I_{11}^G,I_{11}^B]& \cdots & [I_{1W}^R,I_{1W}^G,I_{1W}^B]\\ ⋮& \ddots & ⋮\\ [I_{H1}^R,I_{H1}^G,I_{H1}^B]& \cdots & [I_{HW}^R,I_{HW}^G,I_{HW}^B]\end{array}\right]$$
这种表示方式便于计算机处理，但图像数据通常维度很高（尤其是彩色图片，如 $1000\times 1000$ 像素的图像有 $10^6$ 个元素），这给数据存储和神经网络处理带来了挑战。

二、压缩矩阵

针对复杂的彩色图片，图像压缩是必要的
原始图像矩阵通常包含大量冗余数据（如相邻像素相似），导致文件大小过大，不利于存储或传输。压缩的目标是减少数据量，同时保持视觉质量。
压缩分为两类：

• 无损压缩：保留所有原始数据，如PNG格式，使用矩阵操作（如游程编码）。
• 有损压缩：牺牲少量细节以换取更高压缩率，如JPEG格式，基于矩阵变换（如离散余弦变换）

压缩过程直接操作图像矩阵：
变换编码：将图像矩阵转换为频域表示，减少空间冗余。例如，在JPEG压缩中，图像被分成8×8块，每个块通过离散余弦变换（DCT）转换为系数矩阵。DCT公式为： $$F(u,v)=\frac{2}{N}C(u)C(v)\sum _{i=0}^{N-1}\sum _{j=0}^{N-1}f(i,j)\cos \left(\frac{(2i+1)u\pi }{2N}\right)\cos \left(\frac{(2j+1)v\pi }{2N}\right)$$ 其中$N=8$，$f(i,j)$是原始像素矩阵元素，$F(u,v)$是变换后的系数矩阵元素。
量化：压缩矩阵通过量化表（另一个矩阵）缩放DCT系数，丢弃高频细节（人眼不敏感部分），实现数据压缩。量化公式为： $$Q(u,v)=\text{round}\left(\frac{F(u,v)}{Q_{\text{table}}(u,v)}\right)$$ 其中$Q_{\text{table}}$是预定义的量化矩阵。
编码：量化后的矩阵通过熵编码（如Huffman编码）进一步压缩为二进制流。
关系总结：图像矩阵是压缩的起点，压缩算法生成新的“压缩矩阵”（如DCT系数矩阵），最终输出为压缩文件。解压时，逆过程重建近似原矩阵。
当然这一部分要求线代基础知识，看不懂没有关系，了解即可

三、全连接神经网络的缺陷

全连接神经网络（FCNN）在处理图像时存在严重缺陷，主要源于其结构：

• 参数爆炸问题：在 FCNN 中，每个输入节点（像素）都连接到隐藏层所有节点。设输入大小为 $n$（如图像展平为向量 $x\in {\mathbb{R}}^n$），隐藏层大小为 $m$，则权重矩阵 $W\in {\mathbb{R}}^{m\times n}$ 的参数数量为 $m\times n$。对于 $H\times W$ 的图像，$n=H\times W$（灰度）或 $n=H\times W\times C$（彩色）。例如，$1000\times 1000$ 的 RGB 图像输入，$n\approx 3\times 10^6$，若隐藏层 $m=1000$，参数量高达 $3\times 10^9$，导致训练困难、内存不足。
• 计算效率低下：前向传播的计算复杂度为 $O(m\times n)$，在图像任务中计算量巨大，难以实时处理。
• 缺乏局部性：FCNN 忽略图像的空间结构。每个像素独立处理，无法有效捕捉局部特征（如边缘、纹理），因为相邻像素在计算中不共享权重。
• 过拟合风险高：高参数量使模型容易过拟合小数据集，泛化能力差。
• 无平移不变性：图像中物体位置变化（如猫在左或右）会导致输出剧烈变化，因为权重与绝对位置绑定。

这些缺陷使 FCNN 不适合图像任务，需要更高效的架构。

四、卷积神经网络

为解决 FCNN 的缺陷，卷积神经网络（CNN）被引入。它利用图像的空间局部性和平移不变性：

• 卷积层：使用卷积核（filter）在图像上滑动，计算局部区域的内积。设输入图像 $X\in {\mathbb{R}}^{H\times W\times C}$，卷积核 $K\in {\mathbb{R}}^{F_h\times F_w\times C\times D}$（$F_h,F_w$ 为核大小，$D$ 为输出通道数），输出特征图 $Y$ 的元素为：
  $$Y(i,j,d)=\sum _{m=0}^{F_h-1}\sum _{n=0}^{F_w-1}\sum _{c=0}^{C-1}K(m,n,c,d)\cdot X(i+m,j+n,c)$$
  这实现了权重共享和稀疏连接，大幅减少参数（如 $3\times 3$ 核仅需 $9\times C\times D$ 参数）。
• 优势：
  • 参数高效：卷积核在整张图像共享权重，避免参数爆炸。
  • 局部特征提取：捕捉边缘、角点等局部模式。
  • 平移不变性：物体位置变化不影响特征检测。
  • 层次结构：通过多层卷积和池化，逐步抽象特征（从低级纹理到高级语义）。

CNN 的典型结构包括卷积层、激活函数（如 ReLU）、池化层和全连接层。以下是一个简单 CNN 的 PyTorch 实现示例：

import torch
import torch.nn as nnclass SimpleCNN(nn.Module):def __init__(self, num_classes=10):super(SimpleCNN, self).__init__()# 卷积层: 输入通道3 (RGB), 输出通道16, 核大小3x3self.conv1 = nn.Conv2d(3, 16, kernel_size=3, stride=1, padding=1)# 池化层: 2x2 最大池化self.pool = nn.MaxPool2d(kernel_size=2, stride=2)# 全连接层: 输入尺寸基于图像大小 (假设输入32x32)self.fc = nn.Linear(16 * 16 * 16, num_classes)  # 池化后尺寸减半: 32/2=16def forward(self, x):x = self.pool(torch.relu(self.conv1(x)))  # 卷积 + ReLU + 池化x = x.view(x.size(0), -1)  # 展平x = self.fc(x)return x# 示例用法
model = SimpleCNN()
input_image = torch.randn(1, 3, 32, 32)  # 批大小1, 通道3, 高度32, 宽度32
output = model(input_image)
print(output.shape)  # 输出: torch.Size([1, 10])

此代码展示了 CNN 如何高效处理图像：卷积层提取特征，池化层降维，全连接层分类。CNN 已成为计算机视觉的基石，广泛应用于图像识别、目标检测等任务。

---

总结一下：图像在计算机中是矩阵方式进行存储的，而CNN卷积神经网络能够高效处理图像，下一节我们来详细分析CNN的整体架构