Softplus

函数+导函数

• Softplus函数
  $$\begin{array}{rl}\mathrm{Softplus}(x)& =\ln (1+e^x)\end{array}$$

• Softplus函数导数
  $$\begin{array}{rl}\frac{d}{dx}\mathrm{Softplus}(x)& =\frac{d}{dx}\ln \left(1+e^x\right)\\ & =\frac{1}{1+e^x}\cdot e^x\\ & =\frac{e^x}{1+e^x}\\ & =\frac{e^x}{1+e^x}\cdot \frac{e^{-x}}{e^{-x}}\\ & =\frac{1}{1+e^{-x}}\\ & =\sigma (x)\end{array}$$
  其中，$\sigma (x)=\frac{1}{1+e^{-x}}$ 是 sigmoid 函数。Softplus 处处可导，并且导数恰好是 sigmoid。

---

函数和导函数图像

• 画图

  import numpy as np
  from matplotlib import pyplot as plt# Softplus 函数
  def softplus(x):return np.log1p(np.exp(x))# Softplus 的导数 = sigmoid
  def softplus_derivative(x):return 1 / (1 + np.exp(-x))# 生成数据
  x = np.linspace(-6, 6, 1000)
  y = softplus(x)
  y1 = softplus_derivative(x)# 绘图
  plt.figure(figsize=(12, 8))
  ax = plt.gca()
  plt.plot(x, y, label='Softplus')
  plt.plot(x, y1, label='Derivative (Sigmoid)')
  plt.title('Softplus and Derivative')# 去边框
  ax.spines['right'].set_color('none')
  ax.spines['top'].set_color('none')
  ax.xaxis.set_ticks_position('bottom')
  ax.spines['bottom'].set_position(('data', 0))
  ax.yaxis.set_ticks_position('left')
  ax.spines['left'].set_position(('data', 0))plt.legend()
  plt.savefig('./softplus.jpg',dpe=300)
  plt.show()3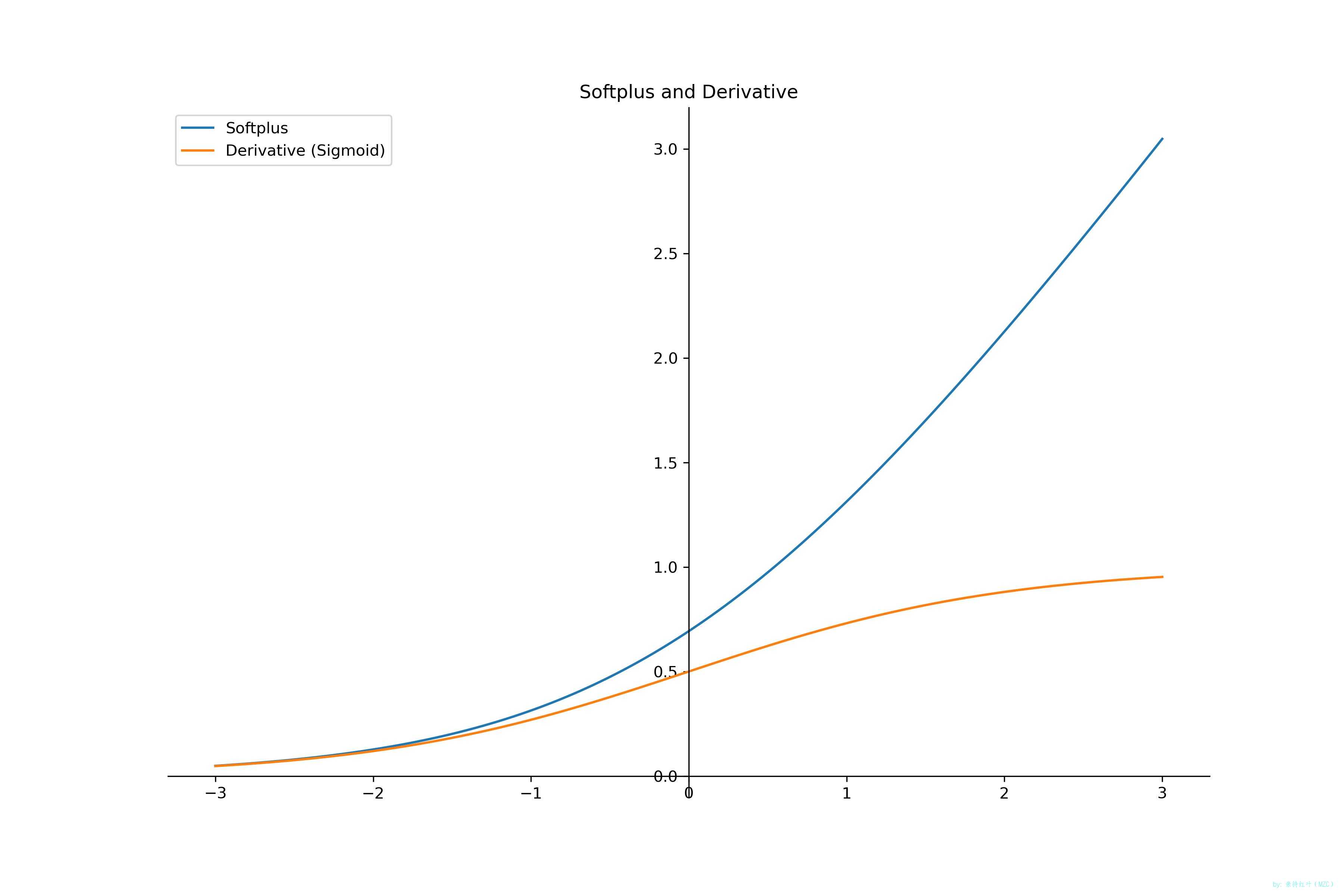
  

  

---

优缺点

• Softplus 的优点

  1. 平滑处处可导：Softplus 是 ReLU 的光滑近似，没有折点，避免了 ReLU 在 0 处不可导的问题。
  2. 梯度不消失：对于任意输入，梯度始终为正，并且随输入增大趋近于 1，有效缓解梯度消失。
  3. 解析形式简单：公式简洁，易于实现，且与 sigmoid 有天然联系。
  4. 连续可导：在需要二阶导数或高阶导数的场景（如 Hessian、自然梯度）中更容易处理。

• Softplus 的缺点

  1. 计算开销：相比 ReLU 的逐位最大值操作，Softplus 需要计算指数和对数，计算量更大。
  2. 输出始终为正：当需要负激活值时（如残差网络中的负值路径），Softplus 无法提供。
  3. 边缘饱和：当输入为很大的负数时，Softplus 会趋于 0，虽然比 sigmoid 缓解，但仍可能带来梯度衰减。
  4. 超参数敏感：在部分任务中需要额外调整初始化或学习率，以抵消其非零均值的副作用。

---

PyTorch 中的 Softplus 函数

• 代码

  import torch
  import torch.nn.functional as F# 使用 PyTorch 自带的 Softplus
  sp = F.softplusx = torch.tensor([-2.0, 0.0, 2.0])
  y = sp(x)print("x :", x)
  print("softplus(x):", y)"""输出"""
  x : tensor([-2.,  0.,  2.])
  softplus(x): tensor([0.1269, 0.6931, 2.1269])
  

---

TensorFlow 中的 Softplus 函数

• 环境

  python: 3.10.9

  tensorflow: 2.19.0

• 代码

  import tensorflow as tfsoftplus = tf.keras.activations.softplusx = tf.constant([-2.0, 0.0, 2.0])
  y = softplus(x)print("x :", x.numpy())
  print("softplus(x):", y.numpy())"""输出"""
  x : [-2.  0.  2.]
  softplus(x): [0.12692805 0.6931472  2.126928  ]
  

---